
курсовая
.docxМетод Лагранжа приведения квадратичной формы к каноническому виду
[править]
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
У этого термина существуют и другие значения, см. Метод Лагранжа.
Метод Лагранжа — метод приведения квадратичной формы к каноническому виду, указанный в 1759 году Лагранжем.
[править] Описание
Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть

есть данная квадратичная форма. Возможны два случая:
-
хотя бы один из коэффициентов aii при квадратах отличен от нуля. Не нарушая общности, будем считать
 (этого
всегда можно добиться соответствующей
перенумерацией переменных);
(этого
всегда можно добиться соответствующей
перенумерацией переменных); -
все коэффициенты
 ,
но есть коэффициент
,
но есть коэффициент
 ,
отличный от нуля (для определённости
пусть будет
,
отличный от нуля (для определённости
пусть будет
 ).
).
В первом случае преобразуем квадратичную форму следующим образом:
![]()
![]()
![]() ,
где
,
где
![]() ,
а через
,
а через
![]() обозначены
все остальные слагаемые.
обозначены
все остальные слагаемые.
![]() представляет
собой квадратичную форму от n-1 переменных
представляет
собой квадратичную форму от n-1 переменных
![]() .
.
С ней поступают аналогичным образом и так далее.
Заметим,
что
![]()
Второй
случай заменой переменных
![]() сводится
к первому
сводится
к первому
Метод вариации произвольных постоянных для построения решения линейного неоднородного дифференциального уравнения
an(t)z(n)(t) + an − 1(t)z(n − 1)(t) + ... + a1(t)z'(t) + a0(t)z(t) = f(t)
Метод состоит в замене произвольных постоянных ck в общем решении
z(t) = c1z1(t) + c2z2(t) + ... + cnzn(t)
соответствующего однородного уравнения
an(t)z(n)(t) + an − 1(t)z(n − 1)(t) + ... + a1(t)z'(t) + a0(t)z(t) = 0
на вспомогательные функции ck(t), производные которых удовлетворяют линейной алгебраической системе

Определителем
системы (1) служит вронскиан
функций z1,z2,...,zn,
что обеспечивает её однозначную
разрешимость относительно
![]() .
.
Если
![]() —
первообразные для
—
первообразные для
![]() ,
взятые при фиксированных значениях
постоянных интегрирования, то функция
,
взятые при фиксированных значениях
постоянных интегрирования, то функция
![]()
является решением исходного линейного неоднородного дифференциального уравнения. Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам.
[править] Метод вариации произвольных постоянных для построения решений системы линейных дифференциальных уравнений в векторной нормальной форме
![]()
состоит в построении частного решения (1) в виде
![]()
где
Z(t) —
базис решений соответствующего
однородного уравнения, записанный в
виде матрицы, а векторная функция
![]() ,
заменившая вектор произвольных
постоянных, определена соотношением
,
заменившая вектор произвольных
постоянных, определена соотношением
![]() .
Искомое частное решение (с нулевыми
начальными значениями при t
= t0
имеет вид
.
Искомое частное решение (с нулевыми
начальными значениями при t
= t0
имеет вид

Для системы с постоянными коэффициентами последнее выражение упрощается:

Матрица Z(t)Z − 1(τ) называется матрицей Коши оператора L = A(t).
Определение квадратичной формы
Квадратичная
форма переменных
![]() -
функция
-
функция

![]() -
коэффициенты квадратичной формы. Без
ограничения общности считают
-
коэффициенты квадратичной формы. Без
ограничения общности считают
![]() тогда
тогда
![]()
Если
переменные
![]() принимают
действительные значения и
принимают
действительные значения и
![]() квадратичная
форма называется действительной.
квадратичная
форма называется действительной.
Матричная запись квадратичной формы
Матрица

называется
матрицей квадратичной формы, ее ранг -
рангом квадратичной формы. Квадратичная
форма называется невырожденной, если
![]()
Главные миноры матрицы A называются главными минорами квадратичной формы.
В
пространстве
![]() квадратичную
форму можно записать в виде
квадратичную
форму можно записать в виде
![]() где
X
- координатный столбец вектора
где
X
- координатный столбец вектора
![]()
В
пространстве
![]() квадаратичную
форму можно представить в виде
квадаратичную
форму можно представить в виде
![]() где
f
- линейный самосопряженный оператор,
матрица которого в некотором
ортонормированном базисе равна A.
где
f
- линейный самосопряженный оператор,
матрица которого в некотором
ортонормированном базисе равна A.
Канонический вид квадратичной формы
Квадратичная
форма называется канонической, если
все
![]() т.
е.
т.
е.
![]()
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.
1.
Ортогональное преобразование пространства
![]() :
:
![]()
где
![]() -
собственные значения матрицы A.
-
собственные значения матрицы A.
2.
Метод Лагранжа - последовательное
выделение полных квадратов. Например,
если
![]()
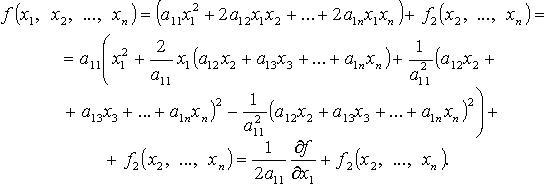
Затем
подобную процедуру проделывают с
квадратичной формой
![]() и
т. д. Если в квадратичной форме все
и
т. д. Если в квадратичной форме все
![]() но
есть
но
есть
![]() то
после предварительного преобразования
дело сводится к рассмотренной процедуре.
Так, если, например,
то
после предварительного преобразования
дело сводится к рассмотренной процедуре.
Так, если, например,
![]() то
полагаем
то
полагаем
![]()
![]()
![]()
3.
Метод Якоби (в случае, когда все главные
миноры
![]() квадратичной
формы отличны от нуля):
квадратичной
формы отличны от нуля):
![]()
Нормальный вид квадратичной формы
Для действительной квадратичной формы
![]()
где
![]() r
= rank A.
r
= rank A.
Для комплексной квадратичной формы
![]() r
= rank A.
r
= rank A.
Для действительных квадратичных форм имеет место закон инерции квадратичных форм: число положительных и число отрицательных квадратов в нормальном виде квадратичной формы не зависит от способа приведения квадратичной формы к нормальному виду с помощью невырожденных линейных преобразований.
Классификация действительных квадратичных форм Положительно-определенные
Квадратичные
формы, для которых
![]() таких,
что
таких,
что
![]() Нормальный
вид
Нормальный
вид
![]() Квадратичная
форма является положительно-определенной
тогда и только тогда, когда все ее главные
миноры положительны
Квадратичная
форма является положительно-определенной
тогда и только тогда, когда все ее главные
миноры положительны
![]() (критерий
Сильвестра).
(критерий
Сильвестра).
Отрицательно-определенные
Квадратичные
формы, для которых
![]() таких,
что
таких,
что
![]() Нормальный
вид
Квадратичная
форма является отрицательно-определенной
тогда и только тогда, когда
Нормальный
вид
Квадратичная
форма является отрицательно-определенной
тогда и только тогда, когда
![]()
Положительно-полуопределенные
Квадратичные
формы, для которых
![]() таких,
что
таких,
что
![]() Нормальный
вид
Нормальный
вид
![]() r
< n,
r
= rank A.
r
< n,
r
= rank A.
Отрицательно-полуопределенные
Квадратичные
формы, для которых
![]() таких,
что
таких,
что
![]() Нормальный
вид
Нормальный
вид
![]() r
< n,
r
= rank A.
r
< n,
r
= rank A.
Неопределенные
Квадратичные
формы, которые принимают как положительные,
так и отрицательные значения. Нормальный
вид:
![]() r
= rank A.
r
= rank A.
