ММДО_МУ по ЛБ(+)

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ

4)

МЕТОДІЧНІ ВКАЗІВКИ до лабораторних робіт з дисципліни

«МАТЕМАТИЧНІ МЕТОДІ ДОСЛІДЖЕННЯ ОПЕРАЦІЙ» для студентів денної форми навчання напряму 6.0804 – «Комп’ютерні науки»

ЗАТВЕРДЖЕНО Кафедрою ШІ Протокол №15 від 18.01.11

Харків 2011

1

Методичні вказівки до лабораторних робіт з дисципліни «Математичні методі дослідження операцій» для студентів денної форми навчання напряму 6.0804 – «Комп’ютерні науки» / Упоряд. А.М. Гвоздинський, В.О. Губін. – Харків: ХНУРЕ, 2011. – 20 с.

Упорядники: А.М. Гвоздинський, В.О. Губін

Рецензент В.П. Авраменко, д-р техн. наук. проф. каф. ІКІ

2

ЗМІСТ

ВСТУП ……………………………………………………………………………..4

1 РОЗВ’ЯЗАННЯ ЗАДАЧ ЛІНІЙНОГО ПРОГРАММУВАННЯ СИМПЛЕКС-МЕТОДОМ…………………………………………………………5

1.1Мета роботи …………….………………………………..…………………...5

1.2Методичні вказівки до самостійної роботи студентів ….……………5

1.3Порядок виконання роботи …………………………………………....10

1.4Зміст звіту ………………………………………………………………10

1.5Контрольні запитання і завдання ………………………………….….10

2 РОЗВ'ЯЗАННЯ ТРАНСПОРТНИХ ЗАДАЧ МЕТОДОМ ПОТЕНЦІАЛІВ………………………………………………..…….12

2.1Мета роботи ……………………………………………………….…....12

2.2Методичні вказівки до самостійної роботи студентів ……………….12

2.3Порядок виконання роботи …………………………………………....15

2.4Зміст звіту …………………………………………………………….…15

2.5Контрольні запитання і завдання ……………………………………...15 3 РОЗВ'ЯЗАННЯ ЗАДАЧ ПРО ПРИ3НАЧЕННЯ…………………..………..….16

3.1Мета роботи……………………………………………………………..16

3.2Методичні вказівки до самостійної роботи студентів …………….....16

3.3Порядок виконання роботи ………………………………………….…17

3.4Зміст звіту …………………………………………………………….…17

3.5Контрольні запитання і завдання ………………………………….…..18

ПЕРЕЛІК ПОСИЛАНЬ………………………………………………………….…19

3

ВСТУП

Дані методичні вказівки призначені для проведення лабораторних робіт з дисципліни «Математичні методи дослідження операцій» для студентів денної форми навчання напряму 6.0804 – «Комп'ютерні науки». Методичні вказівки складені відповідно до навчального плану спеціальності і робочої програми з дисципліни і мають за мету навчити студентів побудові математичних моделей,

проведенню дослідження операцій і пошуку оптимальних рішень з використанням сучасної обчислювальної техніки і програмного забезпечення.

Під час виконання лабораторних робіт студенти закріплюють на практиці й удосконалюють знання та вміння, отримані при вивченні дисциплін

«Математичні методи дослідження операцій», «Основи програмування та алгоритмічні мови», «Об’єктно-орієнтоване програмування».

Під час підготовки до лабораторних робіт необхідно опрацювати конспект лекцій, методичні вказівки до роботи, ознайомитися з літературою,

що рекомендується.

Методичні вказівки містять опис трьох лабораторних робіт. Кожен розділ, що відповідає окремій лабораторній роботі, складається з таких підрозділів: мета роботи, вказівки до самостійної підготовки до лабораторної роботи, порядок виконання роботи, зміст звіту, контрольні запитання і завдання.

4

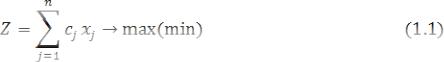
1 РОЗВ'ЯЗАННЯ ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ

СИМПЛЕКС-МЕТОДОМ

1.1 Мета роботи

Мета роботи – закріплення теоретичного матеріалу та оволодіння практичними навичками розв’язання задач лінійного програмування та створення відповідного програмного забезпечення.

1.2 Методичні вказівки до самостійної роботи студентів

Загальна характеристика симплекс-методу.

Симплекс-метод дозволяє переходити від одного припустимого базисного рішення до іншого таким чином, щоб значення цільової функції неперервно збільшувалось. Отже, оптимальне рішення знаходятьза скінченну кількість кроків.

Основою алгоритму симплекс-методу є ідея цілеспрямованого перебору вершин багатогранника планів задачі. При цьому забезпечується збільшення або зменшення цільової функції. Оскільки кількість вершин опуклого багатогранника завжди скінченна, то забезпечується скінченність алгоритму.

Обстеження вершин починається після визначення однієї з них, тобто знаходження початкового опорного плану задачі лінійного програмування

(ЗЛП). Опорний план має задовольняти не менше ніж n лінійно незалежних обмежень, враховуючи й обмеження на знак. Базою опорного плану

X=(x1,x2,…xn) називають т лінійно незалежних векторів,

Алгоритм симплекс-методу поділяють на два етапи: знаходження початкового опорного плану задачі і знаходження оптимального плану, або встановлення факту необмеженості цільової функції на множині планів задачі.

Алгоритм симплекс-методу застосовується лише для канонічної форми ЗЛП, тому задачу в інших формах слід відображати у канонічній.

Загальна постановка ЗЛП

Визначити величини xj ≥0, які максимізують лінійну форму

5

за умов існування обмежень виду

(1.2)

Як зазначено вище, симплекс-метод застосовується лише для канонічної форми ЗЛП. Тому, щоб розпочати розв'язання за допомогою симплекс-методу,

необхідно перетворити систему нерівностей (1.2) в еквівалентну систему рівнянь шляхом введення нових невід'ємних змінних xn+1, xn+2,…, xn+m.

Внаслідок цього система (1.2) набуває такого вигляду:
a11x1+ a12x2+…+a1nxn+ xn+1=b1,
a21x1+ a22x2+…+a2nxn+ xn+1=b2,	(1.3)
--------------------------------------
am1x1+ am2x2+… amnxn+ xn+1=bm,

Введення канонічної форми запису дозволяє автоматично знайти початковий план. Перетворимо систему (1.3) у векторну форму. Для цього введемо такі позначення:

p1=(a11,a21,…,am1), p2=(a12,a22,…,am2),

…

pn=(a1n,a2n,…,amn), p0=(b1,b2,…,bm).

Система (1.3) набуває при цьому такого виду:

або

Щоб цільова функція залишалась незмінною при введенні додаткових змінних, запишемо її у вигляді

Тепер (1.4)–(1.6) запишемо у вигляді симплекс-таблиці. Для цього введемо у початкову таблицю параметри, які відповідають початковому невиродженому опорному плану Х=(х1,х2,...хm,0,…,0)) з базисом pn+1,pn+2,…, pn+m: коефіцієнти при змінних хj у цільовій функції (рядок С); коефіцієнти при базисних змінних хi (стовпець С); базисні змінні (стовпець Х); вектори, які

6

входять у базис(стовпець Б); елементи матриці умов задачі, де xij=aij; xi=bi;

оцінки , що відповідають векторам р1, р2 ,…, рn.

Проаналізуємо таблицю початкового плану. Таблиця 1.1 – Початковий план

Cj

C1

C2

…

Cj

…

Cn

Cn+1

…

Cn+m

i

Б

Сi

X=P0

P1

P2

Pj

Pn

Pn+1

…

Pn+m

1

Pn+1

0

x1

x11

x12

x1j

x1n

1

…

0

2

Pn+2

0

x2

x21

x22

x2j

x2n

0

…

0

…

…

…

…

…

…

…

…

…

…

…

…

…

i

Pn+i

0

xi

xi1

xi2

xij

xin

0

…

0

…

…

…

…

…

…

…

…

…

…

…

…

…

m

Pn+m

0

xm

xm1

xm2

xmj

xmn

0

…

1

m+1

Zj

m+2

Zj-Cj=

Відповідно до введеної раніше термінології у табл. 1.1 маємо початковий план, який виражається базовими векторами pn+1, pn+2 ,…, pn+m і значеннями p0.

Далі виникає запитання: чи не можна одержати більш вигідного плану, ніж початковий. Можливий один і тільки один з таких варіантів:

1)maxZ=, тобто максимальне значення цільової функції необмежено велике, тобто необмежене зверху;

2)maxZ кінцева і отримано оптимальний план;

З) оптимальний план ще не отримано. Тобто можна досягнути плану із ще більшим значенням Z.

Симплекс-метод дає можливість на базі табл. 1.1зробити необхідні висновки:

1)якщо існуєякий-небудьвід'ємнийелемент томає місце1 або2;

2)якщо всі в цьому стовпці (для якого) то справедливе 1.

3)якщодеякі ,то необхідніподальшіобчислення, тобто справедливе3; 4)якщо всі , то досягнутий mахZ, тобто одержано оптимальний

розв'язок.

Ітеративний алгоритм обробки симплекс-таблиць.

Припустимо, що розглядається випадок, коли , крім того, деякі

. Отже необхідні подальші обчислення, тобто виконується умова 3.

7

Аналізуємо рядок m+2 табл. 1.1. в якій здійснюється оцінка плану.

З усіх обираємо найбільш від'ємне число. Тим самим визначається вектор pj=pk, який потрібно ввести до стовпця Б. Стовпець, де знаходиться pj називають ведучим.

Вектор, який слід виключити із базису, знаходять з умови

(1.7)

Із базису виводять вектор р1, на якому досягається найменше значення . Рядок 1 таблиці та елемент х1k називають ведучими. Далі починається перерахування елементів симплекс-таблиці і заповнюється нова таблиця, що

відповідає новому базису pn+1, pn+2 ,…, pk,…, pn+m.
Всі елементи x`ij нової таблиці знаходять зі співвідношень:
x`ij=x1j/x1k, якщо i=1,			(1.8)
x`ij=xij-(x1j/x1k)xik, якщо

а елемент цільового рядка – зі співвідношень z`0=z0-(x1/x1k)

(1.9)

Черговий опорний план перевіряють за цільовим, тобто m+2 рядком.

Якщо в цьому рядку всі то знайдемо оптимальний план. В іншому випадку переходимо до наступної ітерації.

Покращення плану від однієї ітерації до іншої відповідає зміні цільової функціїна (zk ck ). Процес закінчується, коли виконується одна з умов 1 або 2.

Якщо потрібно відшукати мінімум лінійної форми ЗЛП, то умовою оптимального плану буде у цільовому рядку.

Алгоритм симплекс-методу для загального випадку

Якщо система обмежень має нерівності виду «» або «=», то початковий опорний план не може бути знайдений так, як розглядалось вище. У такому разі вводять так звані «штучні змінні». Розглянемо такий випадок:

F(x)=

(1.10)

8

за умов
Ах	(1.11)
х

Якщо всі Ах і немає одиничних векторів, то ЗЛП називається ЗЛП із

«повною штучною базою».

По відношенню до початкової задачі це так звана розширена М-задача.

Вона також розв'язується за допомогою симплекс-методу.

До цільова функції вводиться наперед задане велике число М зі знаком

«+» у випадку мінімізації цільової функції чи зі знаком «–» у випадку

максимізації, як коефіцієнт при невідомих.

Якщо Ах, то при переході до канонічного вигляду буде отримано

систему обмежень такого виду:
a11x1+ a12x2+…+ a1nxn -1 xn+1=b1,
a21x1+ a22x2+…+a2nxn-1 xn+2=b2,	(1.12)
--------------------------------------
am1x1+ am2x2+…+amnxn-1 xn+1=bm.

Додаткові змінні у цій системі не можна використовувати як початковий базис, бо хn+1,…, xn+m<0. Тому необхідно ввести ще один вектор додаткових змінних хn+m+1,…, xn+m+m. Ці змінні не мають нічого спільного з реальною задачею і мають бути виведені з базису якнайшвидше. Щоб гарантувати їх швидке виведення після початку ітерацій, штучні змінні вводять у цільову функцію з коефіцієнтом М.

Штучні змінні створюють початковий розв'язок. Застосовуючи симплекс-

метод, необхідно вивести з базису всі штучні змінні. Якщо від штучних змінних звільнитися не можна, це означає, що задача не має розв'язку, тобто її обмеження суперечливі.

Розширена М-задача має початковий план X0= (0,0,…,0; b1,b2,…,bm) і

визначає систему одиничних векторів Pn+1,…, Pn+m, що створюють базис m-векторного простору, який називається штучним. Усі змінні

також називаються штучними.

Після обчислення всі дані заносять до таблиці, аналогічної табл. 1.1, яка проте містить на один рядок більше, ніж звичайна симплекс-таблиця. При

9

цьому до нього вписують коефіцієнти при М, а в (m+2) рядку – складові, що не містять М.

Обробка симплекс-таблиць здійснюється за допомогою звичайного симплекс-алгоритму.

1.3 Порядок виконання роботи

1 Адаптувати алгоритм розв’язання задач лінійного програмування симплекс-методом для подальшої програмної реалізації.

2.Розробити програмне застосування, що реалізує симплекс-алгоритм розв'язання задач лінійного програмування. Введення вхідних даних має здійснюватися з файлу.

3.Розробити набір тестів, що покривають будь-які випадки при розв'язанні задач лінійного програмування.

Тести мають покривати такі випадки: є один розв'язок, є нескінченна множина розв’язків, розв'язок відсутній у зв'язку :, необмеженістю області допустимих рішень, розв'язок відсутній у зв'язку з несумісністю системи обмежень.

4. Протестувати розроблене застосування та переконатися у коректності його роботи.

1.4 Зміст звіту

Звіт має містити такі дані:

1.Назва роботи

2.Мета роботи

3.Опис особливостей програмної реалізації симплекс-алгоритму.

4.Фрагмент проекту, що реалізує симплекс-алгоритму

5.Результати тестування розробленого застосування по кожному тесту.

6.Висновок роботи.

1.5Контрольні запитання і завдання

1.Назвіть необхідні і достатні умови, при яких ЗЛП має розв’язок.

2.Чи можливо, щоб оптимальний розв’язок знаходився в середині ОПР?

10