
Лабораторная работа №4
«Выполнение арифметических операций»
4.1 Цель работы: Исследовать особенности выполнения арифметических команд в микроконтроллере ATmega128 и пути использования МК для программной реализации обработки информации.
4.2 Теоретическое введение
В процессе разработки прикладных программ для МП систем, построенных на базе МК ATmega128, наибольшие сложности представляет разработка программ вычислительных процедур, связанных с ограничениями, накладываемыми особенностями организации МК, такими как отсутствие в системе команд МК часто используемых операций умножения и деления, малоразрядный формат данных и, следовательно, низкая точность их обработки, ограниченный диапазон представления данных из–за отсутствия команд обработки чисел с плавающей запятой, отсутствие операций десятичной арифметики. Эти ограничения не являются непреодолимыми, однако их преодоление вызывает некоторые затруднения.
Задачей работы, наряду с изучением арифметических команд МК, является рассмотрение в качестве примеров программ и алгоритмов таких вычислительных процедур, как сложение массива однобайтных чисел с получением двухбайтного результата, сложение многобайтных целых чисел без знака, операций умножения и деления
Основные арифметические функции соответствующих команд МК – это сложение и вычитание двух чисел. Команда ADD складывает, а команда SUB вычитает данные регистра Rr из регистра Rd и запоминает результат в регистре Rd. Для учета возможного переполнения МК содержит флаг переноса, который работает как девятый бит регистра. Команда вычитания использует флаг переноса как флаг заема. Если он устанавливается после команды вычитания в "1", то это значит, что число в регистре Rr больше, чем в Rd.
Кроме названных арифметических операций в системе команд МК имеются команды сложения и вычитания с учетом переноса и с непосредственным операндом, расположенным во втором байте команды и т д. Примеры выполнения арифметических команд приведены в задании 1.
Представления целых чисел:
В двоичной системе счисления числа представляются с помощью комбинации единиц и нулей, знака “минус” и знака разделяющей точки между целой и дробной частью числа. Например, десятичное число – 1.312510 в двоичном виде будет выглядеть как – 1001.01012. Но в компьютере мы не можем хранить и обрабатывать символы знака и разделяющей точки – для “машинного” представления чисел могут использоваться только двоичные цифры (0 и 1). Если операция выполняется только с неотрицательными числами, то формат представления очевиден. В машинном слове из 8 бит можно представить числа в интервале от 0 до 255. Например:
00000000 = 0
00000001 = 1
00101001 = 41
10000000 = 128
11111111 = 255
В общем случае n-битовая последовательность двоичных цифр an-1 an-2 …a1 a0 может быть интерпретирована как целое число А, значение которого равно
Прямой код
Существует несколько представлений о едином формате представления как положительных, так и отрицательных чисел. Все их объединяет то, что старший бит слова (с точки зрения европейца – самый левый, или бит, которому при представлении числа без знака должен быть приписан самый большой вес) является битом хранения знака или знаковым разрядом. Все последующие биты слова представляют значащие разряды числа, которые в каждом формате интерпретируются по-своему. Значение 1 в знаковом разряде интерпретируется как представление всем словом отрицательного числа.
Простейшим форматом, который использует знаковый разряд, является прямой код. В n-разрядном двоичном слове n-1 значащих разрядов представляют величину числа. Например:
00010010 = +18
10010010 = -18
Общее правило математически формулируется следующим образом:
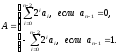
Формат представления чисел в прямом коде неудобен для использования в вычислениях. Поэтому при реализации арифметических операций в АЛУ над целыми числами наиболее широкое применение находит другой формат, получивший наименование дополнительного кода.
Дополнительный код
Как и в прямом, в дополнительном коде старший разряд в разрядной сетке отводится для представления знака числа. Остальные разряды интерпретируются не так, как в прямом коде. В таблице 4.1. перечислены основные свойства дополнительного кода и правила выполнения арифметических операций в дополнительном коде.
Таблица 4.1 Основные свойства дополнительного кода и правила выполнения операций
|
Диапазон представления на n-разрядной сетке |
от -2n-1 до 2n-1 - 1 |
|
Количество кодовых комбинаций, соответствующих числу 0 |
Одна (00000000) |
|
Переход в дополнительный код |
Инвертировать значение в каждом разряде представления исходного числа (положительного или отрицательного), а затем сложить образовавшееся число с числом 00000001 по правилам сложения чисел без знака |
|
Расширение разрядности представления |
Добавить дополнительные разряды слева и заполнить их значениями, равными значению в знаковом разряде исходного представления |
|
Определение переполнения при сложении |
Если оба слагаемых имеют одинаковые знаки (оба положительны или отрицательны), то переполнение возникает в том и только в том случае, когда знак суммы оказывается отличным от знаков слагаемых |
|
Правило вычитания |
Для вычитания числа В из числа А инвертировать знак числа В, как описано выше, и сложить преобразованное число с А по правилам сложения в дополнительном коде |
Рассмотрим n-разрядное двоичное целое число А в дополнительном коде. Если А положительно, то значение его знакового разряда an-1 равно 0. В значащих разрядах будет представлена абсолютная величина числа точно так же, как и в прямом коде:

Очевидно, что диапазон представления положительных чисел n-разрядным дополнительным кодом простирается от числа 0 до числа 2n-1 – 1 (для этого числа значения во всех значащих разрядах равны 1). Для представления большего числа потребуется расширение разрядной сетки.
Теперь перейдем к отрицательным числам. Знаковый разряд an-1 дополнительного кода отрицательного числа А (А<0) равен 1. В n-1 значащих разрядах может содержаться произвольная комбинация нулей и единиц, а также комбинаций может быть 2n-1. Следовательно, имеется потенциальная возможность представить отрицательные числа от -1 до -2n-1. Желательно таким образом установить соответствие между двоичными комбинациями и целыми отрицательными числами, чтобы арифметические операции над ними выполнялись по тем же правилам, что и над числами без знака. В формате целых чисел без знака для вычисления числа по его двоичному представлению следует присвоить старшему разряду в разрядной сетке вес +2n-1. При представлении, включающим и знаковый разряд, это приводит к тому, что желаемые арифметические свойства сохраняются, если вес этого разряда (старшего в разрядной сетке представления) будет равен -2n-1. Это соглашение и используется при представлении чисел в дополнительном коде. Формально для отрицательного числа в дополнительном коде соблюдается соотношение:
Примеры представления чисел в дополнительном коде:
00010010 = +18
11101110 = -18
00000111 = 7
11111001=-7
10001000 = -120
01111000 = 120
01001011 = 75
11001000 = -56
Обратный код получается путём инверсии заданного числа, например:
дано число 10101101, делаем инверсию числа получаем 11010010, причём первая единичка указывает на знак числа (1-- минус, 0 -- плюс) её инверсии не подвергаем.
Дополнительный код путем прибавления к полученному числу 11010010 числа 00000001 получаем 11010011.
Знаковые обратные двоичные коды.
Обратные двоичные коды отличаются от прямых только тем, что отрицательные числа в них получаются инвертированием всех разрядов числа. При этом знаковый и цифровые разряды не различаются. Алгоритм работы с такими кодами резко упрощается.
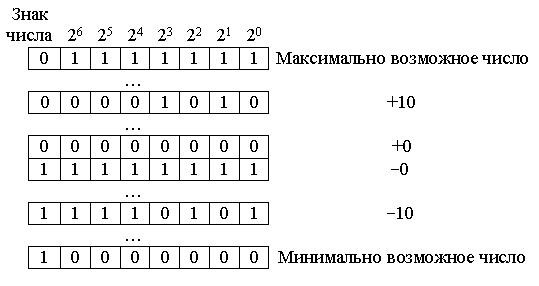
Тем не менее при работе с обратными кодами требуется специальный алгоритм распознавания знака, вычисления абсолютного значения числа, восстановления знака результата числа. Кроме того, в прямом и обратном коде числа для запоминания числа 0 используется два кода, тогда как известно, что число 0 положительное и отрицательным не может быть никогда.
Представление дробных чисел в двоичном коде с фиксированной запятой
Кроме целых чисел часто требуется работать с дробными числами. Следующий вид двоичных кодов, который мы рассмотрим - это дробные коды. Как и в случае целых чисел, дробные числа могут быть беззнаковые и знаковые. Для записи знаковых чисел могут быть использованы прямые, обратные и дополнительные коды. Принцип их построения точно такой же, как и в случае целых чисел.
Рассмотрим, как можно записать дробное число. До сих пор мы предполагали, что двоичная запятая находится правее самого младшего разряда. Но кто сказал, что она должна всегда находиться в этом месте? Мы можем договориться, что запятая находится слева от самого старшего разряда, и тогда в такой переменной можно будет записывать только дробные числа:

Или договоримся, что она находится точно посередине переменной, и тогда мы сможем записывать смешанные числа:

Остальные случаи рассматривать не будем. Они строятся точно так же как и для целых чисел.
