
- •Решение линейных дифференциальных уравнений с постоянными коэффициентами и нулевыми начальными условиями с помощью интегралов Дюамеля
- •Типовой расчет
- •1. По данному графику оригинала найти изображение:
- •2. Найти оригинал по заданному изображению:
- •4. Операционным методом решить задачу Коши:
- •5. Решить систему дифференциальных уравнений:
Лекция 2.
Применение операционного исчисления к решению линейных дифференциальных уравнений и систем уравнений с постоянными коэффициентами
Пусть требуется найти частное решение линейного дифференциального уравнения с постоянными коэффициентами
![]() ,
(1)
,
(1)
удовлетворяющее начальным условиям
![]() ,
(2)
,
(2)
где
![]() - заданные числа.
- заданные числа.
Будем
считать, что искомая функция
![]() вместе с ее производными до
вместе с ее производными до
![]() – го порядка и функция
– го порядка и функция
![]() являются оригиналами.
являются оригиналами.
Обозначим:
![]() и
и
![]() .
Пользуясь свойством дифференцирования
оригинала и свойством линейности,
перейдем в дифференциальном уравнении
от оригиналов к изображениям:
.
Пользуясь свойством дифференцирования
оригинала и свойством линейности,
перейдем в дифференциальном уравнении
от оригиналов к изображениям:
![]()
![]() .
.
или
![]()
![]() .
(3)
.
(3)
Полученное
алгебраическое уравнение, линейное
относительно изображения, называют
операторным
(или уравнением в изображениях). По
найденному из него изображению
![]() ,
можно найти оригинал
,
можно найти оригинал
![]() ,
используя таблицу и свойства преобразования
Лапласа.
,
используя таблицу и свойства преобразования
Лапласа.
Пример 1. Операционным методом решить задачу Коши
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Пусть
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
По таблице оригиналов и изображений
![]() .
.
Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение:
![]() .
.
Разрешим
его относительно
![]() ,
получим
,
получим
![]() .
.
Найдем оригинал для каждого слагаемого в правой части полученного равенства.
![]() .
.
Дробь
![]() нужно представить в виде суммы простейших
дробей.
нужно представить в виде суммы простейших
дробей.
Рациональная
дробь
![]() называется правильной, если степень
называется правильной, если степень
![]() многочлена
многочлена
![]() меньше степени
меньше степени
![]() многочлена
многочлена
![]() ,
т.е.
,
т.е.![]() .
Если дробь неправильная, то можно
разделить числитель на знаменатель и
выделить многочлен и правильную дробь.
Простейшими дробями называются
правильные рациональные дроби вида
.
Если дробь неправильная, то можно
разделить числитель на знаменатель и
выделить многочлен и правильную дробь.
Простейшими дробями называются
правильные рациональные дроби вида
![]() ;
;
![]() ;
;
![]()
![]() .
.
Условие
![]() означает,
что многочлен
означает,
что многочлен
![]() имеет комплексные корни.
имеет комплексные корни.
Любую правильную рациональную дробь можно представить в виде суммы простейших дробей.
Если знаменатель представлен в виде разложения
![]() (4)
(4)
где
![]() и
и
![]() -
кратности соответствующих вещественных
и комплексных корней,
то разложение правильной рациональной
дроби на простейшие будет иметь вид
-
кратности соответствующих вещественных
и комплексных корней,
то разложение правильной рациональной
дроби на простейшие будет иметь вид
 (5)
(5)
Коэффициенты
разложения
![]() находят методом частных значений или
методом неопределенных коэффициентов.
находят методом частных значений или
методом неопределенных коэффициентов.
Дробь
![]() представим в виде суммы простейших
дробей
представим в виде суммы простейших
дробей
![]() .
.
Умножив
обе части последнего равенства на![]() ,
получим
,
получим
![]() .
.
Чтобы
найти неопределенный коэффициент
![]() ,
подставим в это уравнение
,
подставим в это уравнение
![]() .
Тогда
.
Тогда
![]() ,
или
,
или
![]() .
.
Приравнивая
коэффициенты при
![]() ,
,
![]() и
и
![]() в обеих частях тождества, получим систему
линейных уравнений
в обеих частях тождества, получим систему
линейных уравнений

![]() ,
,
из
которой можно найти остальные
неопределенные коэффициенты
![]() и
и
![]() .
Из первого уравнения этой системы
.
Из первого уравнения этой системы
![]() ,
из второго уравнения
,
из второго уравнения
![]() .
Следовательно,
.
Следовательно,

![]() .
.
Таким образом,
![]() .
.
Пример 2. Операционным методом решить систему дифференциальных уравнений с заданными начальными условиями
 ,
,
![]() ,
,
![]() .
.
Решение.
Пусть
 .
Тогда
.
Тогда
 .
.
Так
как
![]() ,
то система операторных уравнений примет
вид
,
то система операторных уравнений примет
вид
 .
.
Получили
систему линейных алгебраических
уравнений относительно изображений
![]() и
и
![]() :
:
 .
.
Найдем
решение системы по формулам Крамера.
Вычислим определитель системы
![]() и вспомогательные определители
и вспомогательные определители
 ,
,
 .
.
Тогда
![]() ,
,
![]() .
.
Частные
решения
![]() и
и
![]() являются оригиналами для вычисленных
изображений. Чтобы найти
являются оригиналами для вычисленных
изображений. Чтобы найти
![]() ,
разложим дробь
,
разложим дробь
![]() на сумму простейших:
на сумму простейших:
![]() .
.
Из этого следует, что
![]() .
.
В
последнем равенстве положим
![]() .
Тогда
.
Тогда
![]() ,
или
,
или
![]() .
При
.
При
![]() :
:
![]() ,
значит
,
значит
![]() .
При
.
При
![]() :
:
![]() ,
откуда
,
откуда
![]() .
Следовательно,
.
Следовательно,

![]() ,
,
![]() .
.
Таким
образом,
 .
.
Решение линейных дифференциальных уравнений с постоянными коэффициентами и нулевыми начальными условиями с помощью интегралов Дюамеля
Если
![]() -
решение уравнения
-
решение уравнения
![]() (6)
(6)
при нулевых начальных условиях
![]() ,
,
![]() ,
…,
,
…,
![]() ,
(7)
,
(7)
то решением уравнения
![]() (8)
(8)
при тех же начальных условиях является функция
![]() .
(9)
.
(9)
Доказательство.
Уравнению (6) при нулевых начальных условиях (7) соответствует операторное уравнение
![]() ,
(10)
,
(10)
где
![]() ,
,
![]() - характеристический многочлен уравнения
(6).
- характеристический многочлен уравнения
(6).
Уравнению (8) при нулевых начальных условиях (7) соответствует операторное уравнение
![]() (11)
(11)
где
![]() ,
а
,
а
![]() .
.
Из (10) и (11) найдем
![]() (12)
(12)
Воспользуемся результатами для изображения по Лапласу интегралов Дюамеля
 (13)
(13)
Положим
в формуле (13)
![]() ,
,
![]() и учтем, что
и учтем, что
![]() .
Тогда получим решение дифференциального
уравнения (8) при нулевых начальных
условиях в виде
.
Тогда получим решение дифференциального
уравнения (8) при нулевых начальных
условиях в виде
![]() (14)
(14)
Формула (14) позволяет находить решение линейного дифференциального уравнения с постоянными коэффициентами при нулевых начальных условиях, не находя изображения правой части этого уравнения.
Типовой расчет
1. По данному графику оригинала найти изображение:

Решение.
Найдем аналитическое выражение для
функции, график которой представлен на
рисунке. Прежде всего запишем уравнение
прямой, проходящей через точки
![]() и
и
![]() ,
и уравнение прямой, проходящей через
точки
,
и уравнение прямой, проходящей через
точки
![]() и
и
![]() .
Как известно, уравнение прямой, проходящей
через точки с координатами
.
Как известно, уравнение прямой, проходящей
через точки с координатами
![]() и
и
![]() имеет вид
имеет вид
![]() .
В данном случае независимая переменная
.
В данном случае независимая переменная
![]() ,
поэтому уравнение прямой примет вид
,
поэтому уравнение прямой примет вид![]() .
Подставляя в это уравнение координаты
точек А и В получим после упрощения
уравнение в виде
.
Подставляя в это уравнение координаты
точек А и В получим после упрощения
уравнение в виде
![]() ,
подставляя в уравнение координаты точек
В и С, получим после упрощения уравнение
в виде
,
подставляя в уравнение координаты точек
В и С, получим после упрощения уравнение
в виде
![]() .
Тогда функция
.
Тогда функция
![]() имеет вид
имеет вид
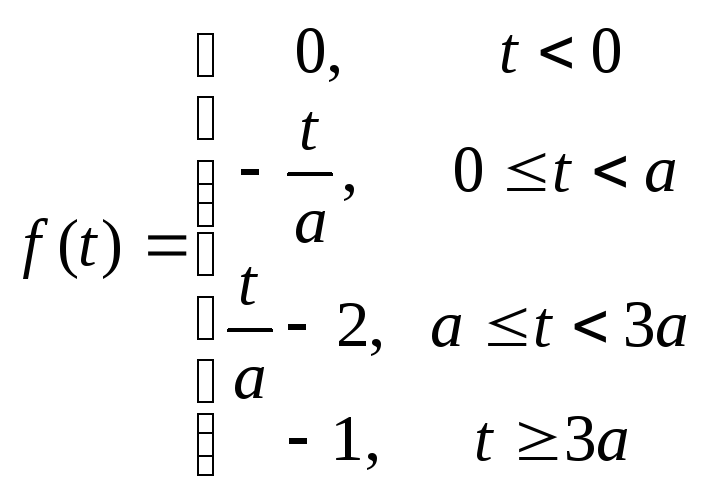 (15)
(15)
Эту функцию можно записать с помощью функции Хевисайда
 (16)
(16)
Построим
график функции
![]() и убедимся, что он совпадает с исходным
заданным графиком
и убедимся, что он совпадает с исходным
заданным графиком

Нужно
преобразовать функцию
![]() к такому виду, чтобы аргументы отдельных
слагаемых, за исключением постоянных,
совпадали с аргументами функций
Хевисайда, содержащихся в этих слагаемых.
Здесь нужно подвергнуть преобразованию
только последнее слагаемое.
к такому виду, чтобы аргументы отдельных
слагаемых, за исключением постоянных,
совпадали с аргументами функций
Хевисайда, содержащихся в этих слагаемых.
Здесь нужно подвергнуть преобразованию
только последнее слагаемое.
![]() (17)
(17)
Тогда
![]()
(18)
Изображение этой функции построим с помощью таблицы, используя теорему запаздывания
![]() (19)
(19)
Решим
теперь эту задачу с помощью Mathcad.
Функция Хевисайда в этом пакете
обозначается греческой буквой
![]() ,
комплексный аргумент изображения
обозначается буквой
,
комплексный аргумент изображения
обозначается буквой
![]() (т.е.
(т.е.![]() ).
).


Полученный результат совпадает с (17).
2. Найти оригинал по заданному изображению:
![]()
Решение.
Для решения этой задачи необходимо
представить дробь
![]() в
виде суммы простейших дробей.
в
виде суммы простейших дробей.
Разложение
дроби
![]() на
простейшие имеет вид
на
простейшие имеет вид
![]() ,
(20)
,
(20)
поскольку
многочлен
![]() имеет
два комплексно сопряженных корня, так
как
имеет
два комплексно сопряженных корня, так
как
![]() .
Приведем сумму дробей в правой части
(20) к общему знаменателю, который совпадает
со знаменателем дроби в левой части
(20). Тогда получим равенство числителей
.
Приведем сумму дробей в правой части
(20) к общему знаменателю, который совпадает
со знаменателем дроби в левой части
(20). Тогда получим равенство числителей
![]() (21)
(21)
Для
определения коэффициентов разложения
в (20), воспользуемся вначале методом
частных значений. Положим в (21)
![]() ,
тогда получим
,
тогда получим
![]() .
.
Для
того, чтобы определить коэффициенты
![]() и
и
![]() ,
используем метод неопределенных
коэффициентов: приравняем коэффициенты
при одинаковых степенях
,
используем метод неопределенных
коэффициентов: приравняем коэффициенты
при одинаковых степенях
![]() и
и
![]() в левой и правой частях равенства (21).
в левой и правой частях равенства (21).
![]() .
Отсюда найдем
.
Отсюда найдем
![]() ,
,
![]() .
.
Следовательно,
![]() .
.
Выделим
полный квадрат в знаменателе
![]() :
:
![]()
. Тогда
 (22).
(22).
Теперь с помощью таблицы по заданному изображению можно восстановить
оригинал
![]()
Для
изображения
![]() с учетом теоремы запаздывания получим
из таблицы оригинал
с учетом теоремы запаздывания получим
из таблицы оригинал
![]()
Следовательно,
![]()
(23)
Приведем решение данной задачи с помощью Mathcad. Для каждого из слагаемых изображения получим оригиналы
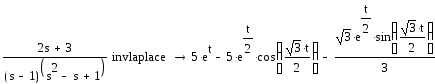

Отсюда для исходного изображения оригинал имеет вид

Этот результат совпадает с (23).
3.
Найти решение дифференциального
уравнения
![]() ,
удовлетворяющее начальным условиям
y(0)
= y'(0)
= 0.
,
удовлетворяющее начальным условиям
y(0)
= y'(0)
= 0.
Для
решения данной задачи используем
интеграл Дюамеля. Найдем вначале решение
![]() дифференциального уравнения
дифференциального уравнения
![]() .
Соответствующее операторное уравнение
для изображения
.
Соответствующее операторное уравнение
для изображения
![]() имеет вид
имеет вид
![]() или
или
![]() .
Отсюда найдем
.
Отсюда найдем
![]() .
Представим полученную дробь в виде
суммы простейших дробей
.
Представим полученную дробь в виде
суммы простейших дробей
![]()
![]() .
Найдем коэффициенты
.
Найдем коэффициенты
![]() .
Для этого приведем дроби в правой части
к общему знаменателю и получим равенство
числителей
.
Для этого приведем дроби в правой части
к общему знаменателю и получим равенство
числителей
![]() (24)
(24)
Для
нахождения коэффициентов вначале
воспользуемся методом частных значений.
Положим
![]() .
Тогда получим
.
Тогда получим
![]() .
Положим
.
Положим
![]() .
Тогда получим
.
Тогда получим
![]() .
Для определения значения
.
Для определения значения
![]() приравняем коэффициенты при степени
приравняем коэффициенты при степени
![]() слева и справа в (24):
слева и справа в (24):
![]() .
Следовательно,
.
Следовательно,
![]() .
Следовательно, изображение имеет вид
.
Следовательно, изображение имеет вид
![]() .
По таблице найдем соответствующий
оригинал
.
По таблице найдем соответствующий
оригинал
![]() ..
Отсюда
..
Отсюда
![]() .
(25)
.
(25)
В
соответствии с формулой (13) решение
исходного дифференциального уравнения
![]() представляет собой интеграл
представляет собой интеграл
![]() ,
(26)
,
(26)
где
![]() -
(27)
-
(27)
правая часть исходного уравнения. Отметим, что в (26) использовано свойство симметрии свертки двух функций.
Подставляя (25) и (27) в (26), получим
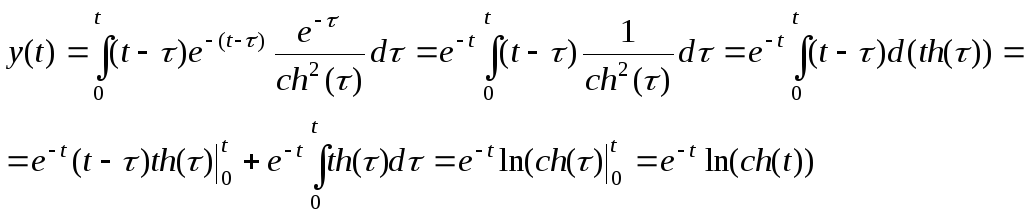 Следовательно,
Следовательно,
![]() .
(28)
.
(28)
Приведем решение данной задачи с помощью Mathcad
Обозначим
![]() через
через
![]() (напомним, что в Mathcad
комплексная переменная
(напомним, что в Mathcad
комплексная переменная
![]() обозначается через
обозначается через
![]() )
)
![]()
Найдем
оригинал
![]() ,
затем положим
,
затем положим
![]() и найдем производную по
и найдем производную по
![]() от функции
от функции![]()
![]()
![]()
![]()
Вычислим
![]() ,
где
,
где
![]() - правая часть исходного уравнения.
- правая часть исходного уравнения.

Правую часть можно упростить
![]()

Этот результат совпадает с выражением (28), полученным ранее.
Учитывая,
что свертка двух функций не зависит от
порядка их следования, можно также
провести расчет
![]() по формуле (26) в виде
по формуле (26) в виде
![]()


В результате получилось довольно громоздкое выражение. Приведем подобные члены в этом выражении и упростим результат

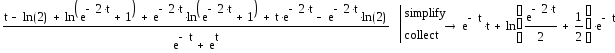
Этот результат также приводится к виду (28)

