Лекция 5. Непрерывные распределения.

Напомним, что непрерывной случайной величиной называется такая, множеством значений которой является интервал или вся числовая ось. Для непрерывной случайной величины существует такая интегрируемая функция, что дляфункция распределения вероятностей имеет вид

(1)

Функция , где, называетсяплотностью вероятности случайной величины или плотностью распределения.

Свойства плотности распределения .

1. Если – непрерывная функция в промежутке, то– дифференцируемая функция и

(2)

как производная от интеграла по верхнему пределу.

2. Плотность вероятности является неотрицательной функцией

,

так как функция является неубывающей функциейи следовательно.

3. .

Это равенство следует из соотношений

.

Эта величина численно равна площади криволинейной трапеции, ограниченной графиком функции , осьюи прямымии. Отсюда также следует, что вероятность того, что непрерывная случайная величина примет заданное значение, равна нулю:.

4. Если – непрерывная функция, то

,

так как .

Величина называется элементом вероятности и представляет собой вероятность того, что случайная величина примет значения, заключенные в промежутке междуи.

5. . Это равенство представляет собой условие нормировки для плотности вероятности и следует из равенства, поскольку. Геометрически условие нормировки плотности вероятности означает, что площадь области, ограниченной графиком плотности распределения и осью абсцисс, равна единице. Она равна вероятности того, что случайная величина примет значения междуи, т.е. вероятности достоверного события.

Примеры непрерывных распределений.

1. Равномерное распределение на отрезке

На отрезок числовой прямой наугад бросают точку, причем считают все положения точки равновозможными. Тогда. Пусть –– алгебра измеримых множеств из и. Тогда.

При каждом , т.е.– случайная величина. Функция распределения этой случайной величины имеет вид

Плотность вероятности равномерного распределения равна

Ниже приведены графики функции распределения и плотности вероятности для равномерного распределения случайной величины

Равномерное распределение используется при генерировании на ЭВМ случайных чисел.

Нормальный закон распределения

Плотность вероятности случайной величины, распределенной по нормальному закону, имеет вид

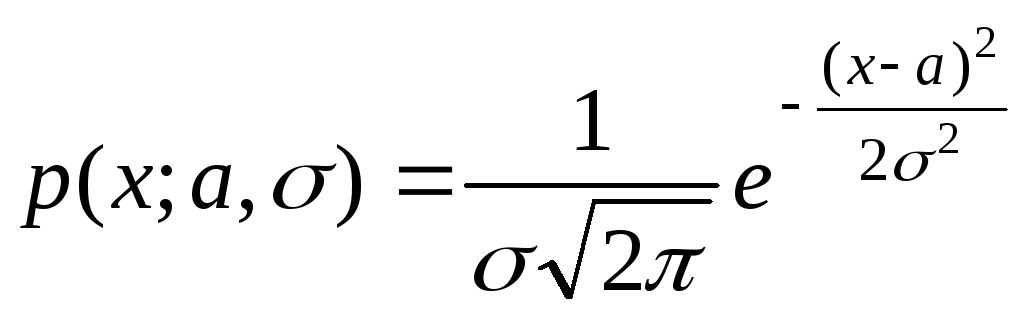(3)

где – параметры распределения:,.Переменнаяможет принимать любые значения.

Впервые это распределение рассмотрел Гаусс при изучении ошибок астрономических наблюдений. Среди законов распределения это распределение встречается наиболее часто, поэтому оно называется нормальным. Нормальный закон хорошо описывает ошибки различных приборов. Причину широкого распространения нормального закона впервые объяснил Ляпунов. Если случайная величина может рассматриваться как сумма большого числа малых слагаемых, то при достаточно общих условиях закон распределения этой случайной величины близок к нормальному независимо от того, по какому закону распределены отдельные слагаемые. А так как практически случайные величины в большинстве своем являются результатом воздействия большого числа различных причин, то этим объясняется популярность этого закона.

Покажем, что функция может рассматриваться как плотность вероятности. Действительно, она неотрицательна и непрерывна. Проверим, что выполняется условие нормировки для этой функции

.

=. Вычислим полученный интеграл

. Отсюда и

. (4)

Этот интеграл называется интегралом Пуассона.

Следовательно,

. (5)

Отсюда получим .

График функции симметричен относительно прямой.

, .

Найдем экстремумы функции . Для этого вычислим первую производную этой функции и найдем ее корни.

Первая производная обращается в нуль при . Вычисли вторую производную функциии найдем ее значение в точке.

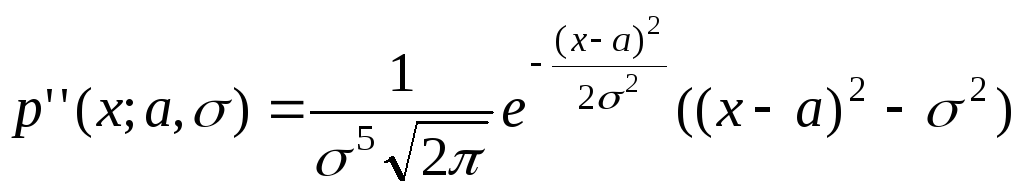
Вторая производная отрицательна в точке . Следовательно, функцияимеет максимум в точке. График плотности вероятности для нормального распределения называется кривой Гаусса. Построим график плотности вероятности для значений.

Отсюда видно, что график функции не меняет своего вида при изменении параметра, а лишь сдвигается вдоль осивлево или вправо. Параметрявляется параметром сдвига.

Найдем теперь точки перегиба графика функции. Для этого найдем корни второй производной и вычислим значения третьей производной в этих точках. Третья производная равна

.

Вторая производная обращается в нуль в точках и. Третья производная в этих точках равна соответственнои. Она отлична от нуля. Значит, найденные точки являются точками перегиба графика функции. Построим графики функциидля значений параметров.

Параметр равен расстоянию между точкой максимума функции и точкой перегиба. Он является мерой «широты» кривой. Чем больше значение, тем меньше величина максимума функции. При уменьшениикривая вытягивается вверх. При этом площадь фигуры под кривой всегда равна единице.

Стандартной нормальной случайной величиной называется случайная величина, распределенная по нормальному закону с параметрами . Плотность распределения стандартной нормальной случайной величины имеет вид

. (6)

Для этой функции существуют подробные таблицы. Плотность вероятности нормального распределения для других значений параметров связана с функцией соотношением

(7)

Функция распределения случайной величины, подчиняющейся нормальному закону, имеет вид

(8)

Эта функция для стандартной нормальной случайной величины, имеет вид

Чаще используется функция

,

которая называется функцией Лапласа. Она связана с соотношением

, так как

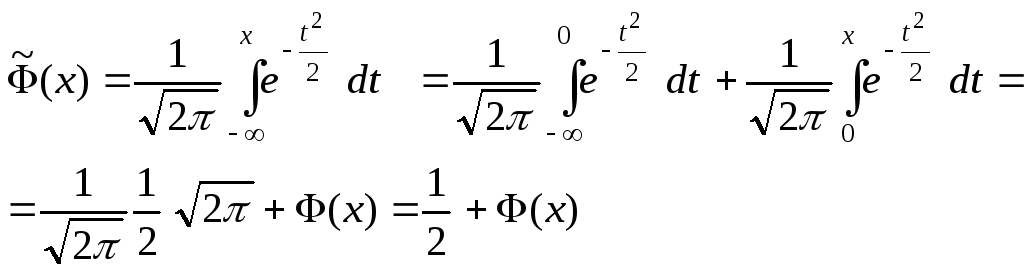
При выводе этого соотношения было использовано значение (5) для интеграла Пуассона и учтена четность подынтегральной функции.

Для функции также существуют подробные таблицы.

Эта функция обладает следующими свойствами: она нечетна ,и.

Иногда используют функцию . Все перечисленные функцииназываются функциями Лапласа. Для этих функций существуют подробные таблицы значений, при использовании которых необходимо учитывать, какая именно функция Лапласа рассматривается.

Функции Лапласа можно выразить через функцию ошибок , которая является встроенной функцией многих математических пакетов. Например,.

Функция распределения выражается через

Построим графики функций для значений параметров.

Вероятность попадания СВ, распределенной по нормальному закону с параметрами в промежутоквычисляется по формуле

, так как

.

Отметим, что

Эту вероятность можно записать также в виде

или

Вероятность попадания нормальной случайной величины с параметрами в промежуток, симметричный относительно параметраопределяется формулой

,

так как

.

Вероятность для СВ, распределенной по нормальному закону, попасть в промежуток равна

,

Вероятность для СВ, распределенной по нормальному закону, попасть в промежуток равна

.