Лекция 7. Предельные теоремы в схеме Бернулли. Локальная и интегральная теоремы Муавра-Лапласа

Пусть случайная величина распределена по биномиальному закону. Эта случайная величина представляет собой число успеховв серии изиспытаний, в каждом из которых может появиться успех с вероятностьюили неуспех с вероятностью.Вероятность того, что в серии изиспытаний появитсяуспехов равна

, (1)

при этом ,.

При больших значениях ивычисление вероятности по формуле (1) представляет значительные трудности. Например, если,,, то

и вычислить такую вероятность достаточно сложно.

,Однако при выполнении определенных условий функция биномиального распределения имеет вид функции нормального распределения или функции Пуассона.

Пусть достаточно велико, ане мало, так что (). Введем обозначение

. (2)

Если при величина, но при этом остается ограниченной величина, т.е., то вероятность того, что в серии изиспытаний будетуспехов равна

, (3)

где .

При достаточно больших эту вероятность можно выразить через функцию

Гаусса :

(3)

где , а аргумент.

Доказательство.

Для случайной величины, распределенной по биномиальному закону, вероятность появления успехов в серии изиспытаний равна

Учитывая, что

, ,, получим

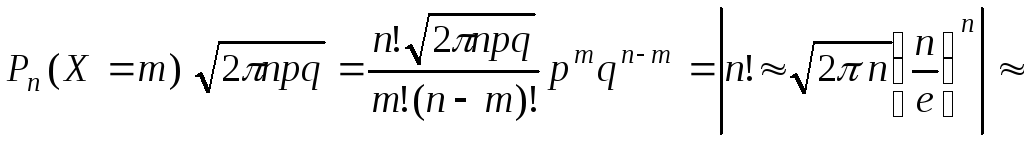
(4)

При получении этого выражения была использована формула Стирлинга , справедливая при достаточно больших значениях.

В формуле (4)

при этом (5)

при этом (6)

при . (7)

Введем . Тогда(8)

С учетом равенств (5) и (6) получим

(9)

При выводе этой формулы было учтено, что и ., что следует из (5) и (6).

Из (9) следует, что , а значит. Подставляя это выражение в (8) и учитывая (5) и (6), получим

(10)

, где .

Из теоремы Муавра-Лапласа следует, что при больших значениях и не малых значенияхфункция биномиального распределения имеет вид функции нормированного нормального распределения си.

, (11)

где

Интегральная теорема Муавра-Лапласа

Если при величина, но при этом остается ограниченной величина, т.е., то вероятность того, что в серии изиспытаний число успехов находится в промежуткеопределяется с помощью функции Лапласа

, (12)

где - функция Лапласа.

Доказательство

(12)

Учитывая, что

и вводя обозначения и,

преобразуем (12) к виду

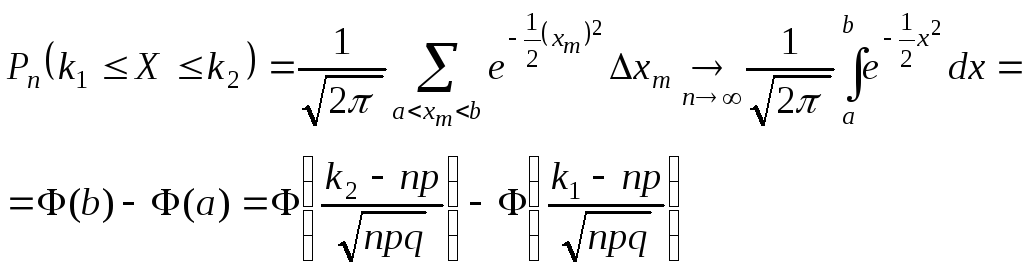(13)

Следовательно, при больших значениях и не малых значенияхфункция биномиального распределения имеет вид функции нормированного нормального распределения си.

Если числа ирасположены симметрично относительно математического ожидания, т.е.и, то формула (13) примет вид

. (14)

Вероятность наступления события не менее, чем заданное число раз

Пример.

Вероятность попадания в цель при одном выстреле равна 0.7. Определить вероятность того, что при 100 выстрелах не менее 75 попадут в цель.

Решение. Здесь ,,,,.

.

Необходимые значения функции Лапласа найдены из таблиц..

Пример

Монету бросают 700 раз. Найти вероятность того, что герб выпадет ровно 350 раз.

Решение.

Рассмотрим случайную величину – количество выпадений герба при 700 бросках. Она распределена биномиально с. Значение, следовательно, можно применить локальную формулу Муавра – Лапласа.

Пример 2.

Монету бросают 700 раз. Найти вероятность того, что количество выпадений герба будет заключено в промежутке от 330 до 370.

Решение.

Рассмотрим случайную величину – количество выпадений герба при 700 бросках. Она распределена биномиально с. Значение, следовательно, можно применить интегральную формулу Муавра – Лапласа.

Пример.

Вероятность того, что изделие относится к первому сорту, равна 0.7 . Партия содержит 10000 изделий. Определить вероятность того, что число изделий первого сорта в этой партии будет заключаться между 6900 и 7100.

Решение. Здесь ,,,,.

Пример.

Вероятность того, что изделие относится к первому сорту равна 0.9 . Партия содержит 1600 изделий. Определить с вероятностью 0.8, в каких границах будет заключаться число изделий первого сорта в этой партии, если эти границы должны быть симметричными относительно математического ожидания.

Решение. Здесь ,,,,.

По формуле (14) . Отсюда.

По таблице значений функции Лагранжа найдем , что значению соответствует значение аргумента. Следовательно,и. Для определения границ, между которыми заключено число изделий первого сорта, имеем неравенство. Отсюда.