
2 АКУСТИКА МОРСКОЙ СРЕДЫ
.docx2 АКУСТИКА МОРСКОЙ СРЕДЫ
2.1. ОСНОВНЫЕ УРАВНЕНИЯ ЗВУКОВОГО ПОЛЯ.
ВОЛНОВОЕ УРАВНЕНИЕ. ПОТЕНЦИАЛ СКОРОСТИ
Жидкие среды, рассматриваемые в гидроакустике, считаются сплошными. Физически это означает, что длина волны, распространяющейся в такой среде, намного превышает размер молекул, а период колебаний — время их свободного пробега между столкновениями. Обычно жидкую среду считают идеальной, пренебрегая её вязкостью и теплопроводностью (движение идеальной жидкости рассматривается как адиабатическое). Однако при изучении поглощения и затухания волн в жидкой среде учитываются её вязкость (внутреннее трение) и теплопроводность.
В идеальной жидкой среде существует только продольная звуковая волна, причём частицы такой среды при плоском её фронте смещаются вдоль направления распространения волны. Со смещением частиц связаны изменения давления (нормального напряжения) р и плотности среды ρ, которые переносятся волной. Звуковая волна (или звуковое поле) в идеальной жидкости характеризуется пятью параметрами:
давлением р,
плотностью ρ
и тремя
составляющими скорости
 (vx,
vy,
vz).
(vx,
vy,
vz).
Давление p складывается из гидростатического давления р0 и звукового давления р1
р = ро+р1 (2.1)
Предполагается, что ро постоянно. Тогда дифференциал dp давления р равен дифференциалу звукового давления, т. е. dp = dp1.
Аналогично имеем для плотности
ρ = ρo + ρ1; dρ = dρ1 (2.2)
где ρо — плотность невозмущенной среды;
ρ1 — плотность, обусловленная звуковой волной.
Первым соотношением, связывающим давление и плотность, является нелинейное адиабатическое уравнение состояния
P = f(ρ). (2.3)
Поскольку изменение давления и плотности малы, то, пользуясь формулой разложения в ряд Тейлора, данное уравнение можно записать в виде
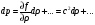 ,
(2.4)
,
(2.4)
где df/dρ — производная по ρ при ρ = ρо, или р = ро, для которой мы ввели следующее обозначение:
df/dρ = с2. (2.5)
Пренебрегая
степенями
 выше первой и интегрируя уравнение
(2.4) в предположении с2
= const,
получаем
линеаризованное уравнение
состояния
выше первой и интегрируя уравнение
(2.4) в предположении с2
= const,
получаем
линеаризованное уравнение
состояния
p = c2ρ + const. (2.6)
Константа исключается при дифференцировании последнего выражения по времени:
 (2.7)
(2.7)
Величина
 есть
скорость звука. Уравнение (2.7) имеет
место лишь тогда, когда можно пренебречь
внутренним трением и когда акустические
скорости частиц малы по сравнению со
скоростями молекул среды.
есть
скорость звука. Уравнение (2.7) имеет
место лишь тогда, когда можно пренебречь
внутренним трением и когда акустические
скорости частиц малы по сравнению со
скоростями молекул среды.
Объём жидкости (τ) должен иметь постоянную массу М, т. е. М = ρτ = const, откуда

Следовательно,

Модуль объёмного сжатия К определяется соотношением
К
= ‒ τ
Таким образом, получаем для скорости звука следующее выражение:
 (2.8)
(2.8)
Второе соотношение между величинами v, ρ и р можно найти, если в жидкости выделить бесконечно малый элементарный объём, который в течение рассматриваемого отрезка времени состоит из одних и тех же молекул и движется вместе с жидкостью. Предположим, что этот элементарный объём движется так, как если бы он был заморожен; тогда к нему можно применить закон Ньютона F = m dv/dt. Получающееся при этом уравнение известно как уравнение Эйлера.
Рис.
2.1. Элементарный объём dx
dy
dz
, используемый
при выводе уравнения Эйлера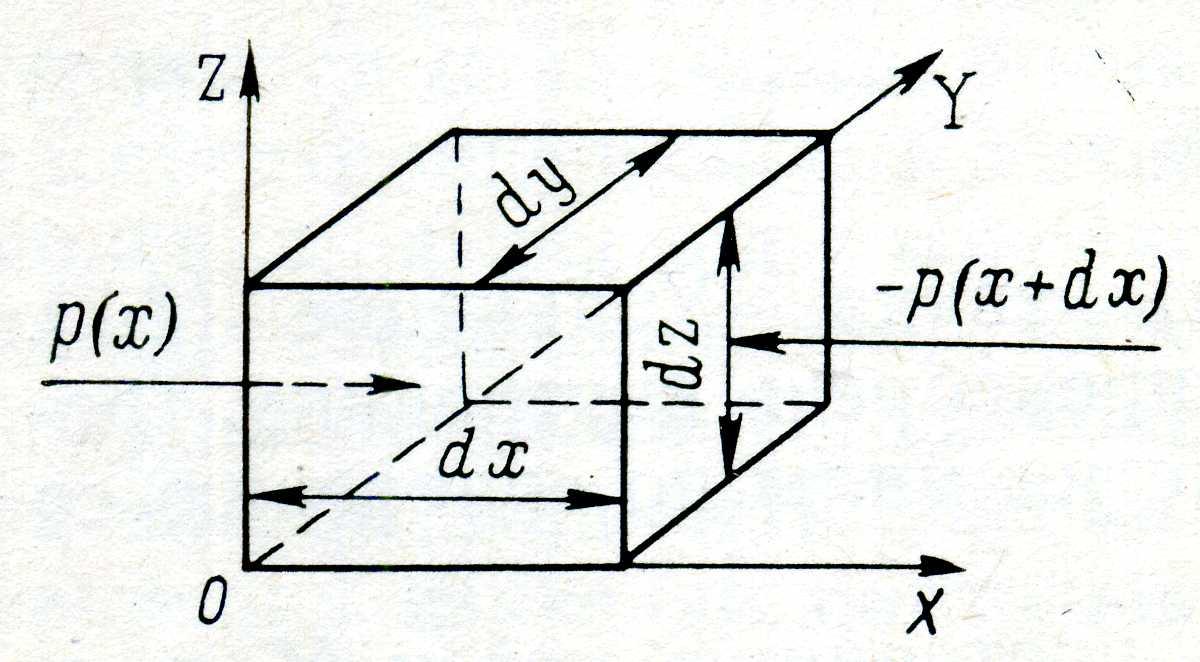
Для вывода уравне-ния Эйлера в случае трёх-мерного движения рас-смотрим элементарный объём dxdydz, имею-щий форму куба (рис. 2.1). Введём обозначения: x1=x; х2 = у; хз = z; v1 = vx; ν2 = vv; v3 = vz. Тогда можно записать
 (i,j
=1,2,3)
,
(2.9)
(i,j
=1,2,3)
,
(2.9)
где подразумевается суммирование по индексам i и j (правило Эйнштейна). Тогда уравнение Эйлера можно записать в следующем виде:
 (2.10)
(2.10)
Первый член в
правой части (2.10) представляет собой
локальное ускорение в некоторой
точке х1,
х2,
хз
жидкости; например, если движение
нестационарно, то скорость в фиксированной
точке будет изменяться во времени.
Второй член в правой части (2.10) представляет
собой конвективное ускорение, т. е.
ускорение, которое приобретают частицы
жидкости вследствие их перемещения
в области с другими значениями скорости.
В силу малости колебательной скорости
ν
в звуковой волне конвективным ускорением,
равным произведению скорости на
производную от скорости по координате,
можно пренебречь по сравнению с локальным
ускорением. Тогда с учётом того, что ρ0
 ρ1
уравнение
Эйлера
примет простой вид
ρ1
уравнение
Эйлера
примет простой вид
 или — grad
p
= ρ0
или — grad
p
= ρ0 (2.11)
(2.11)
Третье соотношение между v, ρ и р — уравнение непрерывности — выражает закон сохранения вещества в гидродинамике: разность между массами жидкости, втекающей за данный промежуток времени в некоторый объём и вытекающей из него, должна быть равна приращению массы жидкости внутри данного объёма.
Будем считать, что
через грань, перпендикулярную оси X
(см. рис. 2.1), за время
dt
втекает
некоторая масса жидкости
тх.
За
этот же промежуток времени
dt
через
противоположную грань вытекает масса
жидкости, отличная от
тх,
а именно
 .
Разность между
указанными массами жидкости будет равна
.
Разность между
указанными массами жидкости будет равна

Так как mx = ρν dy dz dt, то

Разность между массами жидкости, втекающей и вытекающей через грани, перпендикулярные осям y и z, соответственно равна


Для
общей разности
 массы втекающей и вытекающей жидкости
получим
массы втекающей и вытекающей жидкости
получим
 (2.12)
(2.12)
С другой стороны, приращение массы жидкости внутри объёма за время dt равно
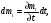
где mt — масса жидкости внутри выделенного объёма в начальный момент времени.
Очевидно, mt = ρ dx dy dz, при этом ρ является переменной величиной. Тогда
 (2.13)
(2.13)
Приравнивая между собой (2.12) и (2.13), получим
 (2.14)
(2.14)
или в векторной форме
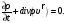 (2.15)
(2.15)
Выражения (2.14) и (2.15) называются уравнениями непрерывности.
Для малых смещений и малых изменений плотности, характеризующих звуковую волну, уравнение (2.15) можно упростить. Введём в это уравнение величину уплотнения s, определяемого выражением
 или ρ
= ρ0(1
+ s).
или ρ
= ρ0(1
+ s).
Подставляя ρ = ρ0(1 + s) в (2.15), получим

или
 (2.16)
(2.16)
Пренебрегая в (2.16) величинами второго порядка малости и используя (2.2), имеем
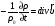 (2.17)
(2.17)
или с учётом адиабатического уравнения состояния (2.7)
 (2.18)
(2.18)
Отметим, что все три уравнения, характеризующие звуковое поле:
адиабатическое уравнение состояния (2.6),
уравнение движения (Эйлера) (2.11)
и уравнение непрерывности (2.17) или (2.18),
— являются линеаризованными вариантами соответствующих уравнений гидродинамики.
Из уравнений
состояния, Эйлера и непрерывности можно
получить волновые уравнения для всех
пяти параметров [р,
ρ,
 (ν1,
ν2,
ν3)],
характеризующих звуковую волну.
(ν1,
ν2,
ν3)],
характеризующих звуковую волну.
Применяя к уравнению Эйлера (2.11) операцию div и дифференцируя уравнение непрерывности по времени, а затем, вычитая один результат из другого, получаем волновое уравнение для давления
 (2.19)
(2.19)
где
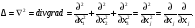 (2.20)
(2.20)
Волновое уравнение для скорости частиц можно получить, заменив операцию grad к уравнению непрерывности и продифференцировав уравнение Эйлера по времени. Поскольку
grad div = div grad + rot rot = Δ + rot rot,
уравнение для скорости частиц принимает вид
 (2.21)
(2.21)
В соответствии с
теоремой Гельмгольца любой вектор
 можно
представить в виде разности градиента
скалярного потенциала Ф
и ротора векторной функции
можно
представить в виде разности градиента
скалярного потенциала Ф
и ротора векторной функции
 :
:
 (2.22)
(2.22)
В
силу того, что звуковое поле в идеальной
жидкости является безвихревым (rot

 0),
0),
 (2.23)
(2.23)
и
с учётом векторного тождества rot
grad
 0 волновое
уравнение (2.21) для колебательной скорости
частиц
0 волновое
уравнение (2.21) для колебательной скорости
частиц
 принимает
вид
принимает
вид
 (2.24)
(2.24)
Введённая нами
скалярная функция Ф носит название
потенциала
скорости.
Подставляя
 = — grad
Ф в уравнение
Эйлера (2.11), получаем связь между звуковым
давлением р1
и потенциалом скорости:
= — grad
Ф в уравнение
Эйлера (2.11), получаем связь между звуковым
давлением р1
и потенциалом скорости:
‒ grad
p1
=

или

 (2.25)
(2.25)
В гармонической звуковой волне частотой ω звуковое давление p1 отличается от потенциала скорости Ф постоянным множителем:
р1 = — i ω ρо Ф, (2.26)
где i — мнимая единица.
Подставляя (2.25) в волновое уравнение для давления и интегрируя его по времени, получаем для потенциала скорости аналогичное уравнение
 (2.27)
(2.27)
