Упражнения.

1. Решить системы уравнений методом обратной матрицы и по формулам Крамера

а) б)

2. Решить системы уравнений методом Гаусса

а) б)

в) г)

3. Исследовать совместность и найти общее решение следующих систем:

а) б)

в) г)

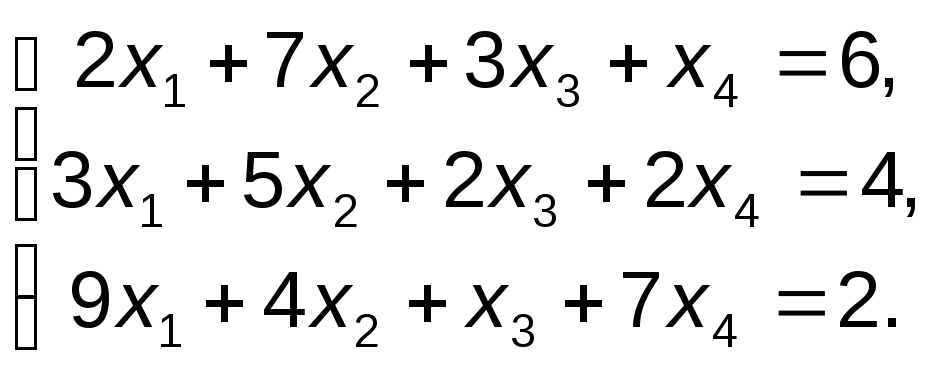д) е)

4. Найти фундаментальную систему решений и общее решение следующих систем:

а) б)

в) г)

д)

5. Найти общее решение неоднородных систем, используя фундаментальную систему решений соответствующих однородных уравнений:

а)б)

6. Определить значения параметра а, при котором система имеет нетривиальные решения, и найти эти решения:

а) б)

Модели Леонтьева и Неймана

1. Модель Леонтьева (1906-1999гг) (В. Леонтьев эмигрировал в США из СССР в 1925г . В 1 963 г. ему была присуждена Нобелевская премия за работы в области экономики).

Первой рассмотрим модель межотраслевого баланса, или модель Леонтьева, американского экономиста.

Пусть весь производственный сектор народного хозяйства разбит на Н чистых отраслей. Чистая отрасль – это условное понятие – некоторая часть народного хозяйства, более или менее цельная (например, энергетика, машиностроение, сельское хозяйство и т.п.)

Пусть a_ij - количество продукции i-й отрасли, расходуемое в j-й отрасли, V_i - объем производства i-й отрасли, c_i - объем потребления продукции i - й отрасли в непроизводственной сфере. Ясно, что

c_i = V_i - a_ij.

Матрица A = (a_ij) содержит весьма много информации, так как ее i – строка характеризует использование продукции i-й отрасли по всему народному хозяйству, а j-й столбец характеризует j-ю отрасль: что и в каких количествах она использует.

Перейдем теперь к безразмерным величинам. Пусть a_ij= a_ij/V_i – это количество единиц продукции i-й отрасли, расходуемое на изготовление, производство одной единицы продукции j - отрасли. Числа a_ij называются коэффициентами прямых затрат i-й отрасли и характеризуют технологию этой отрасли. Число же c_i/v_i есть доля продукции i - отрасли, идущая на непроизводственное потребление.

Для дальнейшего рассмотрения модели Леонтьева сделаем два важных предположения:

Первое состоит в том, что сложившуюся технологию производства считаем неизменной. Таким образом, матрица A = (a_ij) постоянна.

Второе состоит в постулировании свойства линейности существующих технологий, т.е. для выпуска i-й отраслью продукции объема Х надо ресурсов (продукции других отраслей) в количестве xa_ij. Это требование означает, в частности, что каждая отрасль способна произвести любой объем своей продукции при условии, что ей будут обеспечены ресурсы в необходимом количестве. На самом деле это, конечно, не так, ибо производственные возможности всякой отрасли ограничены имеющимся объемом трудовых ресурсов и основных фондов.

Есть много общего в рассматриваемой ситуации с задачей оптимального планирования или оптимального использования ресурсов. В частности, пусть X=(x_i) – вектор объемов производства в отраслях, тогда a_ijx_i - потребляемые объемы продукции этих отраслей, что остается вне производства только C=X-AX. Важнейшим вопросом в рассматриваемой модели является продуктивность модели Леонтьева.

Пусть потребность непроизводственной сферы выражается вектором С. Существует ли вектор производства, обеспечивающий это, т. е. удовлетворяющий уравнению C=AX-X-? Разумеется, с учетом экономической интерпретации, этот вектор производства должен быть неотрицательным. Поэтому говорят, что модель Леонтьева продуктивна, если уравнение AX-X=C имеет неотрицательное решение для любого C0, т.е. матрица А позволяет произвести любой неотрицательный вектор потребления.

ТЕОРЕМА: Модель Леонтьева с матрицей А продуктивна тогда и только тогда, если существует неотрицательная матрица, обратная к матрице (E - A).

Можно доказать также, что модель Леонтьева продуктивна, если она позволяет произвести хоть какой-нибудь строго положительный вектор потребления: из этого вытекает, что можно произвести и любой неотрицательный вектор потребления.

Только что указанные критерии продуктивности модели Леонтьева не имеют хорошей экономической интерпретации.

Рассмотрим еще один критерий продуктивности.

Пусть модель Леонтьева задана матрицей А размерами mn; обозначим через N множество {1,...,n}. Пусть SN говорят, что подмножество S изолированно, если a_ij=0 всякий раз, когда jS, iN-S. Понятие изолированности подмножества S допускает прозрачную экономическую интерпретацию: отрасли, номера которых принадлежит S, не используют товары, производимые в отраслях с номерами, не принадлежащими S.

Матрица называется неразложимой, если в ней нет изолированных подмножеств, кроме N, .

Понятие неразложимости также имеет прозрачный экономический смысл: любая отрасль использует, хотя бы косвенно, продукцию всех отраслей. Ведь если a_ij0, то j-я отрасль непосредственно использует продукцию i-я отрасли . Но если даже a_ij=0, т.е. j-я отрасль не использует продукцию i-й отрасли непосредственно, все равно при неразложимой матрице от данной до любой другой можно найти цепочку отраслей, использующих продукцию друг друга.

Для неразложимых матриц условие продуктивности выглядит так. Если сумма элементов каждой строки не больше единицы и хотя бы для одной строки меньше единицы, то модель Леонтьева с этой матрицей продуктивна.