Преобразование структурных схем

ДЗ – динамическое звено,

ПФ – передаточная функция.

Структурная схема – представление САУ в виде совокупности ДЗ.

Р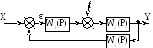ис.2.36. Структурная схема САУ

В прямоугольных блоках – ПФ блоков САУ, состоящие из элементарных ДЗ. Стрелками обозначаются связи между элементами и воздействия: выходное Y, задающее X, возмущающее f. Разветвления сигналов (узлы) обозначаются точками. Сумматоры – . Сумматор 1 вычисляет сигнал рассогласования ε = x – z.

Структурная схема представляет собой математическую модель САУ, состоящую из типовых ДЗ и являющуюся очень удобным, информативным и наглядным представлением САУ.

Для анализа и синтеза САУ необходимо на практике знать математическое описание системы в виде её общей ПФ.

Структурная схема позволяет просто решить эту задачу сворачиванием всей совокупности типовых ДЗ в одно. Для этого применяется 3 правила преобразования структурной схемы и правило переноса узла и сумматора.

Звенья в структурных схемах могут соединяться между собой последовательно, параллельно и встречно на схеме с обратной связью.

Рис.2.37. Структурные схемы соединений звеньев в САУ

1. ПФ цепочки последовательно соединённых звеньев равна произведению их ПФ: . (2.37)

2. ПФ группы параллельно соединённых звеньев равна сумме ПФ: .

3. ПФ группы звеньев, соединённых по схеме с обратной связью, равна отношению ПФ прямой цепи к выражению: 1 “­–” для положительной обратной связи и 1 “+”1 для отрицательной ПФ разомкнутой цепи: (ПФ замкнутой цепи) (2.39).

При положительной обратной связи сигнал обратной связи прибавляется к задающему воздействию, при отрицательной – вычитается из него.

Прямая цепь – совокупность звеньев, передающих сигнал от входа к выходу.

ПФ разомкнутой цепи состоит из ПФ цепи и ПФ обратной связи. В случае одноконтурной САУ ПФ такой цепи равна произведению ПФ всех звеньев.

Р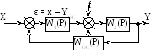ис.2.38. Правило переноса сумматора Рис.2.39. Правило переноса узла

Рис. 2.40. Одноконтурная линейная САУ с ПФ по возмущению, управлению и ошибке

Правило перевода / переноса сумматора и узла.

Определим ПФ по управлению, по возмущению и по ошибке для одноконтурной линии САУ. На основании принципа суперпозиции определим поочерёдно ПФ САУ по входу X и f, считая действующим только 1 из входов. Предполагая ,что f=0,определяем ПФ: (2.40). Аналогично ПФ по возмущению (X=0): . (2.41)

П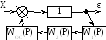Ф по ошибкеε получим после преобразования исходной схемы САУ в вид (f = 0,X = 0).

Рис. 2.41. Структурная схема САУ с ПФ по ошибкеε

ПФ прямой цепи между входным воздействием и сигналом ошибки равна 1, тогда ПФ САУ по ошибке: (2.42).

Анализируя ПФ (2.40-2.42) для случая, когда на линейную систему подаётся несколько воздействий z, на основании суперпозиции можно определить зависимость выходного сигнала от совокупности входящих: 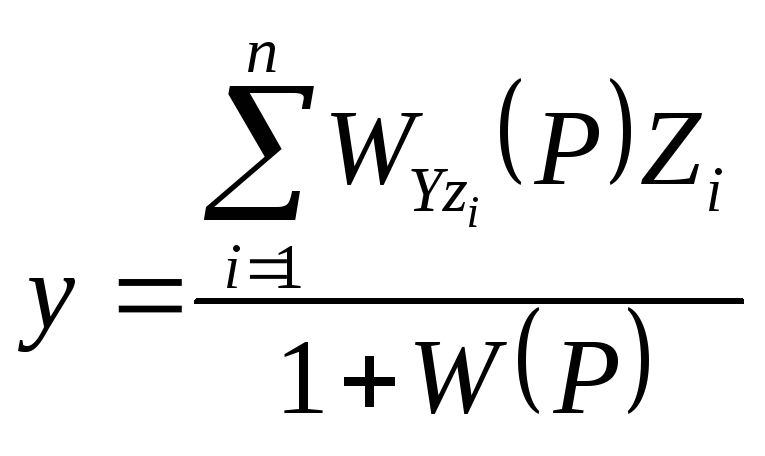. Отсюда для рассматриваемой системы получаем:(2.43). Эти уравнения используются для исследования всех САУ.

Применяя рассмотренные правила преобразования структурной схемы, можно любую многоконтурную схемы привести к одноконтурному виду и свернуть в 1 ДЗ, ПФ которого будет являться ПФ исходной многоконтурной системы.

2. Методика применения ИКО к выбору параметров САУ с заданной структурой.

1. Вычисление ИКО колебательного переходного процесса по экспериментальным данным.

2. Определение передаточных функций разомкнутых и замкнутых систем по задающему

В ТАУ получили широкое применение методы математического описания, основанные на понятии передаточной функции (ПФ). Она является наиболее удобной формой записи линейных уравнений звеньев и самой САУ. При этом используется 2 формы ПФ: в операторном виде и в виде изображения Лагранжа.

Для получения ПФ в операторном виде в ДУ (2.2) необходимо заменить: ,P – оператор дифференцирования, тогда уравнение (2.2) будет:

. (2.7)

Определяем отношение выходной величины к исходной:

. (2.8)

ПФ звена /системы в операторном виде представляет собой отношение двух полиномов – оператора воздействия (числитель) и собственного полинома (знаменатель) (характеристический полином).

При получении ПФ с помощью преобразований Лапласа необходимо, чтобы входное воздействие X(t) удовлетворяло условиям: X(t) = 0, t < 0, (2.9),c - абсцисса абсолютной сходимости. В этом случае преобразование Лапласа для X(t)имеет вид:

(2.10).

Если все члены (2.2) при нулевых начальных условиях умножить на e^st и проинтегрировать от 0 до ∞, то: ,

(2.11), или в виде ПФ: (2.12).

Согласно (2.12) передаточной функцией непрерывной линейной стационарной системы называется отношение преобразования Лапласа Y(s) к преобразованию Лапласа X(s) при нулевых начальных условиях.

Сходство между (2.8) и (2.12) очевидно. Если система нестационарная, то коэффициент ДУ – функция времени и (2.12) будет неверно.

Для стационарных звеньев САУ: W(P) = W(s).

ПФ полностью характеризует динамические и статические свойства системы. Зная ПФ системы и вид воздействия, можно определить переходные процессы на выходе системы.

Динамические свойства системы определяет характеристическое уравнение, которое получается при приравнивании к 0 полинома знаменателя (характеристического полинома).

Нули ПФ – приравнивания 0 полинома числителя, т.е. значения корней, при которых ПФ обращается в 0.

Полюсы ПФ – нули характеристического полинома (ПФ = ∞).

Для исследования свойств динамических систем используется типовые воздействия. Реакция системы на единичное ступенчатое воздействие при нулевых начальных условиях называется переходной функцией: h(t) = y(t) при x(t) = 1, y(0) = 0 (2.13).

Реакция системы на единичное импульсное воздействие (δ-функция) при нулевых начальных условиях называется импульсной переходной функцией / функцией веса, т.е.

ω(t) = y(t) при (2.14). Функции (2.13, 2.14) представляют собойвременные характеристики: .

Для определения связи между временными характеристиками системы и её ПФ используют следующие равенства: . (2.15)

Подставим первое выражение в (2.12): , (2.16)

т.е. ПФ является прямым преобразованием Лапласа от импульсной переходной функции или импульсная переходная функция является обратным преобразованием Лапласа от передаточной функции.

Т.о. подавая на вход системы («чёрный ящик») единичное воздействие (импульсное) на выходе получим импульсную переходную функцию.

Представив реакции на выходе системы в виде ММ и применив к ней прямое преобразование Лапласа, получим ПФ, т.е. полностью определим динамические свойства САУ.

Аналогично можно поступить по отношению к единичному ступенчатому воздействию, используя второе выражение из (2.15): (2.17).

ПФ устойчивых ДЗ и систем обладает следующими свойствами:

1. ПФ W(s) представляет собой дробно-рациональную функцию вида (2.12), причём порядок m не превышает порядка n;

2. Все коэффициенты a, b ПФ вещественны. Это следует из того, что они представляют собой функции параметров системы, т.е. может быть только вещественным;

3. Корни полинома числителя и знаменателя (полюса) ПФ могут быть только комплексно-сопряжёнными;

4. Все полюса ПФ W(s) располагаются в левой полуплоскости комплексной плоскости, что является условием устойчивости системы;

5. При s = jω ПФ (2.12) преобразуется в амплитудно-фазовую частотную характеристику системы, при s = 0 – в передаточный коэффициент для звеньев.