
2_glava_21_03
.docxГлава 2 Подпространства, линейные оболочки, фактор пространства
Предложение 2.1. Непустое множество М векторов в пространстве V называется подпространством, если операции умножения и сложения на число не выводят из множества V, то есть если множество V по отношению к этим операциям само является линейным пространством.
Очевидно, что вектор 0 входит в любое подпространство и множество V0, состоящее из одного этого вектора, является подпространством. Оно называется нулевым подпространством.
Само пространство V также, как следует из выше сказанного, является подпространством. Подпространства V0 и V называются тривиальными подпространствами.
Так
как каждое подпространство M
само по себе является линейным
пространством, то можно говорить о
размерности подпространства

Пример 2.1 Рассмотрим в пространстве V любую конечную систему векторов:
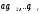 (2.1)
(2.1)
и обозначено через Vh множество всех тех векторов, которые являются линейными комбинациями векторов.
Доказательство 2.1. Докажим данное положение, что М будет линейным подпространством. Действительно, если:
 (2.2)
(2.2)
то
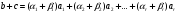 (2.3)
(2.3)
следовательно
вектор
 принадлежит
к М; к М принадлежит и вектор:
принадлежит
к М; к М принадлежит и вектор:
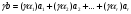 (2.4)
(2.4)
при
любом значении числа
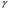 .
.
Замечание 2.1. Размерность линейного подпространства М не больше размерности n самого пространства V, причем равна n лишь при V=M. Размерностью нулевого подпространства следует считать конечно, элемент 0.
Предложение 2.3. Для всякого k, 0<k<n, в пространстве V существуют линейные подпространства размерности k - достаточно взять подпространство, порожденное любой системой из k линейно независимых векторов.
Предложение Пусть в пространстве V даны линейные подпространства М' и М''. Совокупность М0 векторов, принадлежащих как к М', так и к М'', будет, как легко проверить, линейным подпространством; оно называется пересечением подпространств. M=M'∩M''
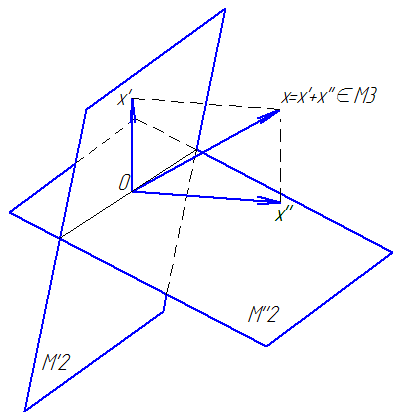
Рисунок 2.1 - Пересечение подпространств
Часто рассматриваются множества всех подпространств, имеющих те или иные свойства.
Если подпространство М0 из М не содержится ни в каком другом подпространстве из М, то его называют максимальным.
Если
же подпространство
 содержит любое подпространство из М,
то его называют наибольшим.
содержит любое подпространство из М,
то его называют наибольшим.
Если же в М существуют наибольшее подпространство, то она также является максимальным.
Пример 2.2. В качестве примера линейного подпространство рассмотрим множество VF всех подпространств, содержащих некоторое множество векторов F. Пересечение всех подпространств, принадлежащих VF, также принадлежит VF и, следовательно, является наименьшим из подпространств множества VF. Оно называется линейной оболочкой множества F и обозначается V(F).
Линейной оболочкой системы векторов называется множество их всевозможных линейных комбинаций в M.
Следствие 2.1. Линейная оболочка векторов является подпространством М.
Предложение
2.4.
Легко проверить, что линейная оболочка
является линейным подпространством в
М. Линейную оболочку
 также называют подпространством,
натянутым на векторы
также называют подпространством,
натянутым на векторы
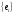 или порожденным векторами системы
или порожденным векторами системы
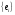 .
Оболочку можно еще определить как
пересечение всех линейных подпространств
в множестве М, содержащих все
.
Оболочку можно еще определить как
пересечение всех линейных подпространств
в множестве М, содержащих все
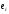 .
Отсюда также выделяется понятие ранга
системы векторов - это размерность его
линейной оболочки.
.
Отсюда также выделяется понятие ранга
системы векторов - это размерность его
линейной оболочки.
Предложение
2.5.
Пересечение множества подпространств
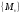 есть наибольшее подпространство,
содержащееся во всех подпространствах
есть наибольшее подпространство,
содержащееся во всех подпространствах
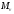 .
.
Введем двойственное понятие к этому определению. Им окажется не объединение потому, что мы будем действовать в классе подпространств, а не в классе всех подмножеств множества М.
Суммой
подпространств
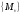 называется наименьшее подпространство,
содержащее все
называется наименьшее подпространство,
содержащее все
 .
.
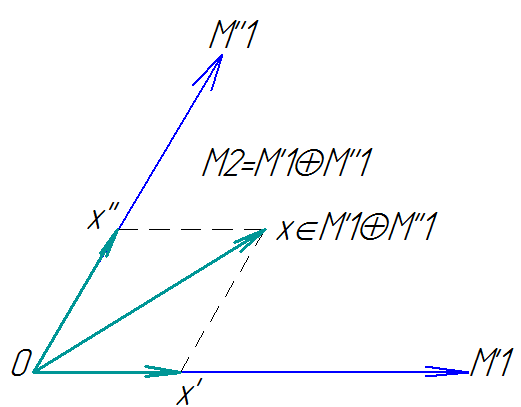
Рисунок 2.2 - Сумма подпространств
Доказательство
2.3.
Очевидно, сумма подпространств
 совпадает с линейной оболочкой
совпадает с линейной оболочкой
 .
.
Сумма
подпространств обозначается обычными
символами
 .
Например:
.
Например:
 (2.5)
(2.5)
В
данном неравенстве (2.1) знак равенства
может быть достигнут тогда только, когда
одно из подпространств
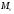 содержит все остальные.
содержит все остальные.
Пусть
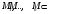 - линейные подпространства в множестве
V,
сумма тогда выражается формулой:
- линейные подпространства в множестве
V,
сумма тогда выражается формулой:
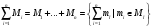 (2.6)
(2.6)
Предложение
2.7.
Если размерности подпространств М',
М'',
М0
и M
суть, соответственно, d1,
d2,
d0
и
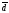 ?
то имеет место следующая формула:
?
то имеет место следующая формула:
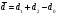 (2.7)
(2.7)
т.е. размерность суммы двух подпространств равна сумме размерностей этих подпространств минус размерность их пересечения.
Доказательство 2.4. Для этого возьмем произвольную базу:
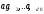 (2.8)
(2.8)
подпространства М0 и дополняем ее до базы:
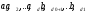 (2.9)
(2.9)
подпространства М' и до базы:
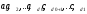 (2.10)
(2.10)
подпространства М''.
Легко видеть, используя определение подпространства M, что это подпространство порождается системой векторов:
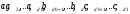 (2.11)
(2.11)
Выше приведенная формула (2.6) будет, следовательно, доказана, если мы докажем линейную независимость системы согласно формуле (2.11).
Отсюда, пусть имеет место равенство:
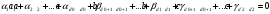 (2.12)
(2.12)
с некоторыми числовыми коэффициентами. Тогда:
 (2.13)
(2.13)
Левая
часть этого равенства содержится в М',
правая - в М'',
поэтому вектор d,
равный как левой, так и правой части
этого равенства, принадлежит к М0
и, следовательно, линейно выражается
через базу по формуле (2.8). Правая же
часть равенства (2.13) показывает, что
вектор d
линейно выражается и через векторы
 .
.
Отсюда,
в соответствии с линейной независимостью
системы (2.9), вытекает, что все коэффициенты
 равны 0, то есть d=0,
тогда ввиду линейной независимости
системы (2.8), все коэффициенты
равны 0, то есть d=0,
тогда ввиду линейной независимости
системы (2.8), все коэффициенты
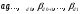 также равны нулю. Этим доказана линейная
независимость системы (2.10).
также равны нулю. Этим доказана линейная
независимость системы (2.10).
Следовательно положение доказано.
Доказанное сохраняет силу и в том случае, если подпространство М0 является нулевым, то есть d0=0.
Пример
2.3.
Проверим
пространство V
является ли суммой подпространства М',
порожденного векторами
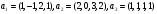 .
.
А
также подпространства М'',
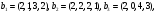 и найти проекцию вектора
и найти проекцию вектора
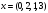 на М'
параллельно М''.
на М'
параллельно М''.
Решение:
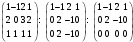
Таким образом, dimM'=2 , а в качестве базиса пространства М' можно взять векторы а1 и а'2=(0,2,-1,0). Найдем теперь размерность и базис подпространства М'':

Таким
образом, dimM''=2
, а в качестве базиса пространства М''
можно взять векторы b1
и
 .
Видно, что
dimM'+
dimM''=4.
.
Видно, что
dimM'+
dimM''=4.
Найдем теперь размерность пространства M'+ M'':

Видно
что dim(M'+
M'')=4.
С учетом сказанного ранее, отсюда
вытекает, что M=
M'+
M''.
Объединяя найденные ранее базисы
подпространств М'
и М'',
получаем, что векторы
 образуют базис пространства V.
Разложим вектор
образуют базис пространства V.
Разложим вектор
 по этому базису:
по этому базису:

Отсюда,
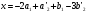 .
Следовательно, проекцией вектора х на
М'
параллельно М''
является вектор
.
Следовательно, проекцией вектора х на
М'
параллельно М''
является вектор
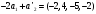 .
.
Пересечение и сумма подпространств подчиняются следующим принципам обрыва, вытекающим из принципа обрыва цепей.
Предложение 2.8. Для любого множества подпространств существует конечное подмножество с тем же самым пересечением.
Подпространства отвечают следующим аксиомам:
Пусть М' есть М1, тогда М'' – М2 .
Предложение 2.9. Сумма двух подпространств М1, М2 есть множество векторов вида:
 (2.10)
(2.10)
Данное положение автоматически может быть применено на сумму любого конечного множества подпространств.
Пример
2.4.
Пусть
G
- произвольное векторное пространство.
Очевидно, что все пространство G
и множество V={0}
являются подпространствами в М, причем
G
- наибольшее подпространство в М.
Следующее простое наблюдение показывает,
что
 - наименьшее подпространство в М.
- наименьшее подпространство в М.
Решение:
Так как нулевой вектор содержится в
любом подпространстве M пространства
V.
Если
x - произвольный вектор из G,
то по второму условию из определения
подпространства
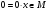 .
.
Пример 2.5. Рассмотрим пространство G, которое, как отмечалось выше, можно отождествить с обычным трехмерным пространством.
Решение: Пусть G - множество векторов, коллинеарных некоторой плоскости . Ясно, что сумма двух векторов, коллинеарных , и произведение вектора, коллинеарного , на любое число коллинеарны . Следовательно, M - подпространство в G. Аналогично доказывается, что множество векторов, коллинеарных некоторой прямой l, также является подпространством в М.
Предложение 2.10. Для любых двух подпространств М1, М2 имеет место равенство:
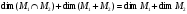 (2.11)
(2.11)
Данную аксиому иначе называют формулой Грассмана. Отсюда следует, что если М1, М2 конечномерного линейного пространства М, то размерность суммы подпространств равна сумме их размерностей без размерности их пересечения.
Доказательство
2.5.
Докажем
данную аксиому,
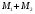 является линейной оболочкой объединения
базисов М1,
М2
и потому конечномерно;
является линейной оболочкой объединения
базисов М1,
М2
и потому конечномерно;
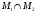 содержится в конечномерных линейных
пространствах М1,
М2.
содержится в конечномерных линейных
пространствах М1,
М2.
Положим,
что
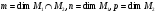 .
Выберем базис
.
Выберем базис
 пространства
пространства
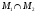 .
По первой аксиоме пространство можно
дополнить до базисов М1,
М2:
пусть это будет
.
По первой аксиоме пространство можно
дополнить до базисов М1,
М2:
пусть это будет
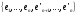 и
и
 .
Назовем такую пару базисов в М1,
М2
- согласованной.
.
Назовем такую пару базисов в М1,
М2
- согласованной.
Отсюда
можно доказать, что семейство
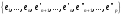 составляет базис пространства
составляет базис пространства
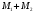 .
Тогда будет верно утверждение аксиомы:
.
Тогда будет верно утверждение аксиомы:
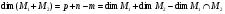 (2.12)
(2.12)
То есть размерность суммы двух подпространств равна сумме размерностей этих подпространств минус размерность их пересечения.
Так
как каждый вектор из
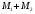 есть сумма векторов из М1,
М2,
то есть сумма линейных комбинаций
есть сумма векторов из М1,
М2,
то есть сумма линейных комбинаций
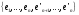 и
и
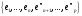 ,
объединений этих семейств порождает
,
объединений этих семейств порождает
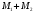 .
Поэтому остается лишь проверить его
линейную независимость. Предположим,
что существует нетривиальная линейная
зависимость:
.
Поэтому остается лишь проверить его
линейную независимость. Предположим,
что существует нетривиальная линейная
зависимость:
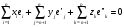 (2.13)
(2.13)
Тогда
обязательно должны существовать индексы
j
и k,
для которых
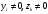 ,
иначе бы получили бы нетривиальную
линейную зависимость между элементами
базиса М1
или М2.
,
иначе бы получили бы нетривиальную
линейную зависимость между элементами
базиса М1
или М2.
Следовательно,
ненулевой вектор
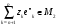 должен лежать также в М1,
либо он равен
должен лежать также в М1,
либо он равен
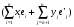 .
Значит, этот вектор лежит в
.
Значит, этот вектор лежит в
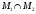 и потому представим в виде линейной
комбинации векторов
и потому представим в виде линейной
комбинации векторов
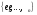 ,
составляющих базис
,
составляющих базис
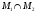 .
Но это представление дает нетривиальную
линейную зависимость между векторами
.
Но это представление дает нетривиальную
линейную зависимость между векторами
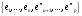 ,
что противоречит их определению.
Следовательно утверждение аксиомы (2)
доказана.
,
что противоречит их определению.
Следовательно утверждение аксиомы (2)
доказана.
Пример 2.6. В пространстве V радиус-векторов с общим началом в точке 0 заданы подпространства: М0, М1, М2 - три множества радиус-векторов, принадлежащих пересекающимся в точке 0 прямым l0, l1, l2 соответственно; П1 и П2 - два множества радиус-векторов, принадлежащих пересекающимся плоскостям 1 и 2 соответственно; прямая l1, при надлежит плоскости 1, прямая l2 принадлежит плоскости 2, плоскости 1 и 2 пересекаются по прямой l0. Найти суммы и пересечения каждых двух из указанных пяти подпространств.
Решение:
Найдем
сумму
 .
Складывая два вектора, принадлежащих
М0
и М1
соответственно,
получаем вектор, принадлежащий плоскости
П1.
На оборот, любой вектор
.
Складывая два вектора, принадлежащих
М0
и М1
соответственно,
получаем вектор, принадлежащий плоскости
П1.
На оборот, любой вектор
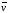 ,
принадлежащий П1,
можно представить в виде
,
принадлежащий П1,
можно представить в виде
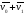 ,
построив проекции
,
построив проекции
 и
и
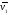 вектора
вектора
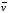 на прямые l0
и l1
соответственно.
Значит, любой радиус-вектор плоскости
П1
раскладывается по подпространствам М0
и М1,
то
есть
на прямые l0
и l1
соответственно.
Значит, любой радиус-вектор плоскости
П1
раскладывается по подпространствам М0
и М1,
то
есть
 .
Аналогично получаем, что
.
Аналогично получаем, что
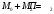 ,
а
,
а
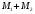 -
множество радиус-векторов, принадлежащих
плоскости, проходящей через прямые l1
и l2.
-
множество радиус-векторов, принадлежащих
плоскости, проходящей через прямые l1
и l2.
Найдем
сумму
 .
Любой вектор
.
Любой вектор
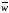 пространства М можно разложить по
подпространствам М2
и П1.
В самом деле, через конец радиус-вектора
пространства М можно разложить по
подпространствам М2
и П1.
В самом деле, через конец радиус-вектора
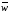 проводим прямую, параллельную прямой
l2,
т.е. строим проекцию
проводим прямую, параллельную прямой
l2,
т.е. строим проекцию
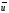 вектора
вектора
 на
плоскость П1.
Затем на М2
откладываем
вектор
на
плоскость П1.
Затем на М2
откладываем
вектор
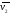 так, чтобы
так, чтобы
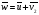 .
Следовательно,
.
Следовательно,
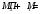 .
Так как
.
Так как
 ,
то
,
то
 .
Аналогично получаем, что
.
Аналогично получаем, что
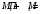 .
Остальные суммы находятся просто:
.
Остальные суммы находятся просто:
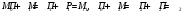 .
(2.14)
.
(2.14)
Заметим,
что
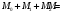 .
.
Используя
аксиому, проверим, например, равенство
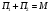 по размерности. Подставляя
по размерности. Подставляя
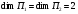 и
и
 в формулу Грассмана, получаем
в формулу Грассмана, получаем
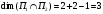 ,
что и следовало ожидать, так как
,
что и следовало ожидать, так как
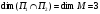 .
.
Пересечения подпространств находим, как пересечение геометрических фигур:
 (2.15)
(2.15)
где
 - нулевой радиус-вектор
- нулевой радиус-вектор
 .
.
Предложение 2.11. Из выше приведенной формулы Грассмана вытекает:
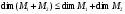 (2.16)
(2.16)
Условиями
достижения равенства в данной аксиоме
выступает следующее: назовем подпространства
М1,
М2
взаимно независимыми (а систему
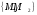 - независимой), если:
- независимой), если:
 (2.17)
(2.17)
Сумма
двух взаимно независимых подпространств
М1,
М2
называется
прямой суммой и обозначается М1+М2.
Отсюда принимаем условие
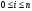 .
.
Доказательство
2.6.
Докажем данную аксиому, необходимость
условий следует из включений
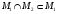 ,
,
 по условиям аксиомы (2). Для того чтобы
доказать достаточность выберем
по условиям аксиомы (2). Для того чтобы
доказать достаточность выберем
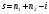 линейно независимых векторов в М:
линейно независимых векторов в М:
 и обозначим через М1,
М2
линейные оболочки
и обозначим через М1,
М2
линейные оболочки
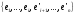 и
и
 соответственно. Согласно аксиомам (2),
(3), проверяется утверждение, что
соответственно. Согласно аксиомам (2),
(3), проверяется утверждение, что
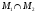 есть линейная оболочка
есть линейная оболочка
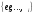 .
.
Предложение 2.12. Для того чтобы имело место равенство:
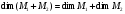 (2.18)
(2.18)
необходимо
и достаточно, чтобы подпространства
М1,
М2
является прямой тогда и только тогда,
когда представление (2.10), единственно
для каждого
 (достаточно даже, чтобы это представление
было единственным для х=0, то есть чтобы
из х=0 следовало х1=0,
х2=0).
(достаточно даже, чтобы это представление
было единственным для х=0, то есть чтобы
из х=0 следовало х1=0,
х2=0).
Понятию
взаимной независимости двойственно
понятие полноты. Система двух подпространств
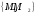 называется полной, если:
называется полной, если:
M1+M2=V (2.19)
то есть если для каждого вектора x=V существует представление (2.19).
Подпространства
М1,
М2
называются взаимно дополнительными, а
система
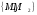 - базисной, если согласно (2.17), то есть
если данная система
- базисной, если согласно (2.17), то есть
если данная система
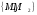 полна и независима. При этом каждое из
подпространств называется дополнением
другого. равенство (2.17) означает, что
каждый вектор х представим, и притом
единственным образом, в виде (2.19).
полна и независима. При этом каждое из
подпространств называется дополнением
другого. равенство (2.17) означает, что
каждый вектор х представим, и притом
единственным образом, в виде (2.19).
Доказательство
2.7.
Докажем данную аксиому, можно дополнить
до базисов
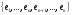 и
и
 пространства V.
Так как существует линейное отображение
f:
V→M1,
переводящее
пространства V.
Так как существует линейное отображение
f:
V→M1,
переводящее
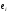 в
в
 для всех i.
Это отображение обратимо и переводит
для всех i.
Это отображение обратимо и переводит
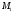 в
в
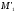 .
Следовательно все линейные подпространства
одинаковой размерности одинаково
расположены внутри пространства V
.
.
Следовательно все линейные подпространства
одинаковой размерности одинаково
расположены внутри пространства V
.
Предложение
2.13.
Для любого подпространства М существует
дополнение. Оно не единственно, если
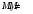 .
То есть Дополнение подпространства М
называется множество М1
всех векторов, относящихся к подпространству
М.
.
То есть Дополнение подпространства М
называется множество М1
всех векторов, относящихся к подпространству
М.
Доказательство
2.7.
Докажем
данную аксиому, если V
- конечномерное пространство, то для
любого подпространства
 можно
выбрать подпространство
можно
выбрать подпространство
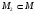 ,
что
,
что
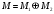 ;
кроме тех тривиальных случаев
;
кроме тех тривиальных случаев
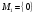 или
или
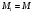 этот выбор неоднозначен. В самом деле,
выбрав базис
этот выбор неоднозначен. В самом деле,
выбрав базис
 в М1
и продолжив его до базиса
в М1
и продолжив его до базиса
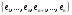 в М, можно взять в качестве М2
линейную оболочку векторов
в М, можно взять в качестве М2
линейную оболочку векторов
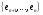 .
.
Пример 2.7. Найти ортогональное дополнение подпространства М, натянутого на векторы а1 = (1, 1, 1, 1), а2 = (–1, 1, –1, 1), а3 = (2, 0, 2, 0).
Решение:
Для того чтобы вектор
 был
ортогонален подпространству, необходимо
и достаточно, чтобы он был ортогонален
векторам системы образующих этого
подпространства. Пусть х
= (х1,
х2,
х3,
х4),
запишем условие ортогональности этого
вектора векторам а1,
а2,
а3:
(х,
а1)
= 0, (х,
а2)
= 0, (х,
а3)
= 0.
был
ортогонален подпространству, необходимо
и достаточно, чтобы он был ортогонален
векторам системы образующих этого
подпространства. Пусть х
= (х1,
х2,
х3,
х4),
запишем условие ортогональности этого
вектора векторам а1,
а2,
а3:
(х,
а1)
= 0, (х,
а2)
= 0, (х,
а3)
= 0.
В координатной форме эти условия представляют собою однородную систему линейных уравнений:
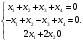 (2.20)
(2.20)
Множество решений этой системы представляет собою подпространство М1, ортогональное подпространству М.
Решая систему, получим фундаментальный набор решений: с1 = (–1, 0, 1, 0), с2 = (0, –1, 0, 1). Эти векторы образуют базис множества решений системы, то есть базис М1, т. о. М1 = М(с1,с2), dimМ1 = 2.
Предложение
2.14.
Размерность любого дополнения
подпространства М равна
 .
.
Величина
 называется коразмерностью подпространства
М и обозначается
называется коразмерностью подпространства
М и обозначается
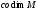 .
Таким образом, по определению:
.
Таким образом, по определению:
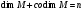 (2.21)
(2.21)
Пример
2.8.
В пространстве V
полиномов степеней
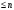 каноническим базисом можно взять систему
мономов
каноническим базисом можно взять систему
мономов
 ,
то есть
,
то есть
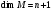 .
Координатами полинома в этом базисе
будут теперь коэффициенты формулы
Тейлора:
.
Координатами полинома в этом базисе
будут теперь коэффициенты формулы
Тейлора:
 (2.22)
(2.22)
Понятие коразмерности двойственно понятию размерности. Что отчетливо видно из следующей аксиомы.
Предложение
2.15.
Если М1,
М2
- подпространства и
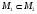 ,
тогда:
,
тогда:
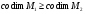 (2.23)
(2.23)
Знак
равенства достигается только тогда,
когда
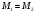 .
.
Доказательство 2.8. Докажем данную аксиому, что введенные операции действительно удовлетворяют аксиомам линейного пространства и не зависят от выбора представителей классов смежности.
Размерность фактор-пространства V/M называется коразмерностью подпространства M в пространстве V.
Если
коразмерность некоторого подпространства
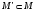 есть конечное число n,
то в M
можно выбрать систему элементов
есть конечное число n,
то в M
можно выбрать систему элементов
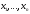 таких,
что всякий элемент
таких,
что всякий элемент
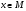 будет иметь единственное представление
вида:
будет иметь единственное представление
вида:
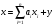 (2.24)
(2.24)
где
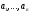 -
некоторые числа и
-
некоторые числа и
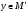 .
.
Решение:
Пусть
 - два класса смежности.
- два класса смежности.
Доказательство 2.9. Докажем, что сумма классов не зависит от выбора представителей. Возьмем в каждом классе по два представителя:

Рассмотрим следующие вектора:
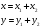
и найдем разность между ними:
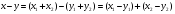
По определению класса смежности:
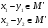
А так как M - подпространство линейного пространства, то и:
x – y € M
Предложение
2.16.
Таким образом, элементы
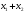 и
и
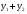 принадлежат одному классу смежности,
а значит определение суммы для классов
смежности действительно не зависит от
выбора представителей.
принадлежат одному классу смежности,
а значит определение суммы для классов
смежности действительно не зависит от
выбора представителей.
Доказательство
2.10.
Докажем, что определение умножения
класса смежности на число не зависит
от выбора представителя. Пусть дан класс
смежности
![]() и
число
и
число
![]() .
Выберем двух представителей класса:
.
Выберем двух представителей класса:
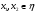
Нужно доказать, что вектора:
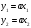
принадлежат одному классу смежности. Вычислим их разность:
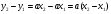
По определению класса смежности:
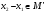
но
так как
![]() является
линейным пространством, то:
является
линейным пространством, то:
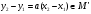
Таким образом, определение операции умножения класса смежности на число не зависит от выбора представителя.
Доказательство 2.11. Докажем теперь, что для фактор-пространства с указанными операциями выполняются свойства линейного пространства.
Начнем
с того, что укажем нулевой элемент
фактор-пространства. Нулевым элементом
фактор-пространства является
подпространство
![]() .
Для доказательства этого факта нужно
показать, что для любого класса смежности
.
Для доказательства этого факта нужно
показать, что для любого класса смежности
![]() имеет
место равенство:
имеет
место равенство:
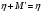 .
.
Это
равенство означает, что существуют
такие вектора
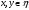 и
и
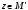 ,
что:
,
что:
