Методички / Вектор.Алг.в.электр

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ДАЛЬНЕВОСТОЧНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

ВЕКТОРНАЯ АЛГЕБРА Практикум

Методические указания по проведению практических занятий для студентов технических специальностей

1.1 Векторы. Линейные операции над векторами. Деление отрезка в данном отношении.

Вектором называется направленный отрезок у которого известны

точка начала A и

точка конца

B. Обозначается АВ, AB.

Через BA

обозначают вектор, направленный противоположно вектору

AB

.

Если заданы

координаты

точек

начала

A1(x1, y1, z1)

и конца

A2(x2, y2, z2) вектора

, то

координаты

вектора

определяются по

AB

формуле:

(x2 x1,

y2 y1, z2 z1)

AB

(1.1)

Модулем или длинной вектора называют расстояние между его началом

. Если

ax; ay; az , то

AB

и концом и обозначают

AB

ax2

a2y

az2

AB

(1.2)

Векторы, параллельные некоторой прямой, называются коллинеарными. Векторы, параллельные одной плоскости, называются компланарными.

Два вектора называются равными, если они: 1)коллинеарны, 2) соноправленны, 3) равны по длине.

Произведением вектора а ax; ay; az на вещественное число

b

a

называется

вектор

b

a

длина которого

равна

,

а

направление

совпадает с направлением вектора

a

,

если 0,

и

противоположно ему, если 0. Координаты вектора определяются по формуле:

b

a

( ax; ay; az )

(1.3)

Т.е. при умножении вектора на число, каждая его координата умножается на это число.

Суммой векторов a1, a2,..., an называется вектор, обозначаемый a1 a2 ... an, начало которого находится в начале первого вектора a1, а

конец в конце последнего вектора an ломанной линии (правило замыкания ломанной). (Рис. 1.1).

a2

a

3

a

4

a

5

a1

a1 a2 ... a5

Рис. 1.1

2

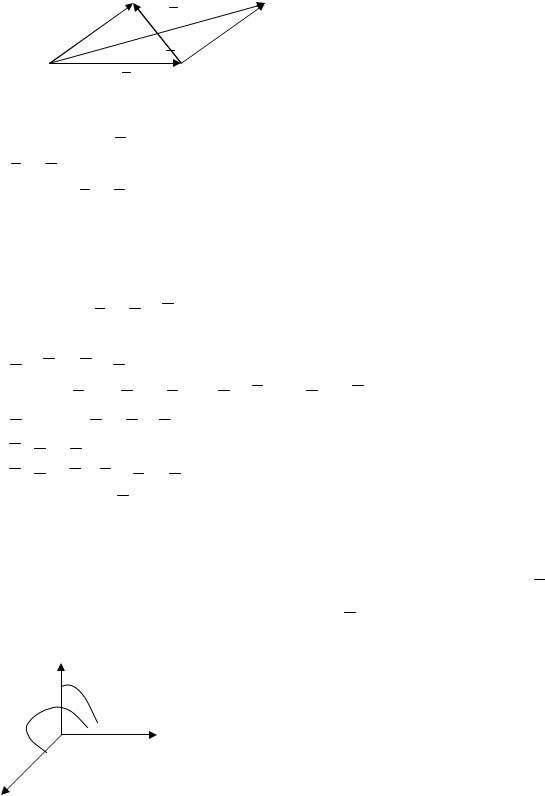
В случае суммы двух векторов оно равносильно

правилу

параллелограмма (Рис. 1.2).

a

b

b

a

b

a

Рис. 1.2

Если векторы

a

и

заданы своими координатами, то координаты

b

вектора

c

a

b

определяются по формуле :

c

a

b

(ax bx; ay by; az bz )

(1.4)

т.е. при сложении векторов их соответствующие координаты складываются.

Аналогично определяется разность векторов, как разность соответствующих координат:

c

a

b (ax bx; ay by; az bz )

(1.5)

Линейные операции над векторами удовлетворяют свойствам:

1. a b b a - коммутативность;

2. a a a, a b a b - дистрибутивность;

3.a 1 a a a 0;

4.1 a a ;

5.0 a 0 , 0 a a.

Всякий вектор a образует с координатными осями Ox, Oy, Oz углы

, , -соответственно. Углы связаны соотношением:
cos2 cos2 cos2 1	(1.6)

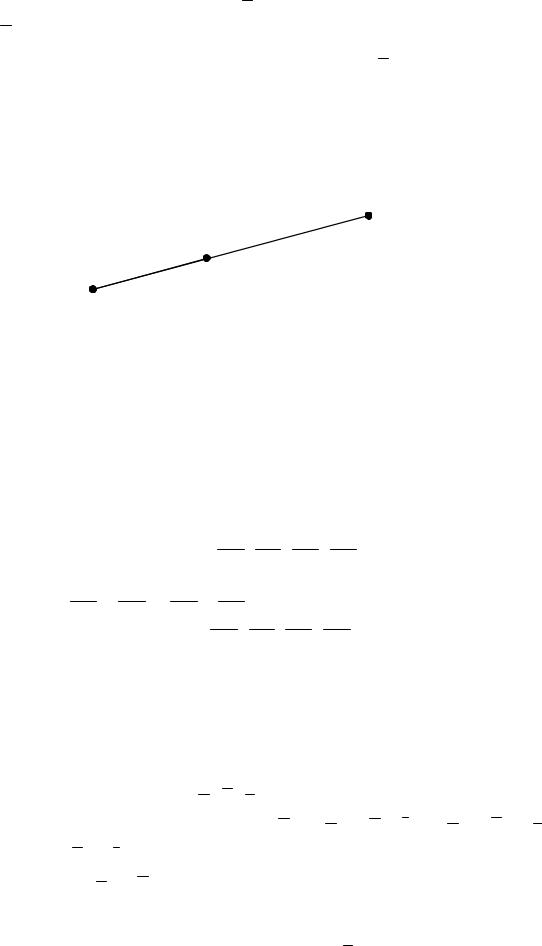
cos , cos , cos - называются направляющими косинусами вектора a и

являются координатами нормированного вектора a0.(Рис. 1.3)

z

y

x

Рис. 1.3

a

ay

a

a0

(cos ; cos ; cos )

x

;

;

z

(1.7).

a

a

a

3

Произвольный вектор

a

можно

записать

в

координатной

форме

a

ax; ay; az

или

линейной комбинацией

базисных векторов

i

(1; 0; 0),

j

(0;1; 0), k (0; 0;1):

a

axi

ay j azk

M x, y,

z делит отрезок

M1M2

Отношение

, в котором

точка

(Рис. 1.4) удовлетворяет равенству

M1M

MM2

(рис.1.4).

M2 x2;y2;z2

M x;y;z

M1 x1;y1;z1

Рис. 1.4

которое задается соотношением:

x

x1

x2

,

y

y1

y2

, z

z1

z2

(1.8).

§1.2 Практикум.

1.1.Даны координаты точек A и B. Вычислить:

1)координаты векторов AB, BA, OA, OB, где точка O– точка начала координат;

2)найти OA OB и OB OA сравнить результаты с п.1;

3)найти модули векторов AB, BA, OA, OB.

1)	A(3; 2),	B(2; -1);	2)	A(-3; 1), B(-2; 5);
3)	A(4; -1), B(3; -2);		4)	A(-1; 2), B(3; 8);
5)	A(5; 4),	B(-3; 1);	6)	A(9; -3), B(7; 4);
7)	A(2; 7),	B(-1; 5);	8)	A(-1; 4), B(5; 3);
9)	A(-3; 5), B(4; -2);		10) A(7; -2); B(5; -3).

1.2.Даны векторы a, b, c . Вычислить:

1)координаты и модуль векторов d 2a 4b , f a 3b 3c записать

векторы d и f линейной комбинацией базисных векторов;

2)векторы a и b являются сторонами параллелограмма. Найти длину его диагоналей (использовать действия сложения и вычитания векторов

(рис 1.2));

3)найти направляющие косинусы вектора c.

4

1)	a				(1; 1; 0),					b (0; 7; 4),															c			( 1; 2; 6);
2)			a		( 3; 5;1),						b									(4; 2; 1),								c			(6;5; 3);
3)			a		(3,1, 2),										b						(5, 3,8)					,			c		(1, 4, 6);
4)			a		(1, 1, 0),							b							(2, 7, 4)					,		c			(5, 3, 1);
5)			a		(0, 2, 1),																b		(3, 7,	5)						,		c	(4, 2, 1);
6)			a		(7,8, 0),				b						( 4, 3, 5)									,		c			(1, 2, 3);
7)			a		(5,1, 0),			b							(7, 2,1)									,		c			(3, 4, 5);
8)			a		( 5, 2, 0),										b					(6, 3, 1),									c	(7, 4, 2);
9)			a		(1, 3,8),									b					(2, 4,1),										c	( 1, 0, 3);
10)				a		(4, 9,1),													b			(5, 3, 2),											c	( 4, 0, 5);

1.3.Вектор AB составляет с координатными осями Ox,Oy,Oz углы

, , соответственно. Вычислить координаты вектора AB, если:

1)

300,

1200,

AB

2;

2)

600,

300,

AB

3;

3)

300, 1200,

4;

4)

300,

600,

2;

AB

AB

5)

1200, 600,

4;

6)

600, 300,

2;

AB

AB

300, 1200,

3;

1200,

300,

4;

7)

AB

8)

AB

1200, 300,

2;

30 0 , 600,

4;

9)

AB

10)

AB

1.4. Даны две вершины A и B параллелограмма ABCD и точка

пересечения его диагоналей E. Найти:

1) координаты остальных вершин;

A

B

2)

отрезок

ограниченный

точками

и

разделен точками

M1, M2, M3, M4

на пять

равных

частей.

Найти координаты точек

Mi, M j.

1)

A(7, 8, 0),

B( 4, 3, 5),

E(1, 2, 3),

i 3,

j 4;

2)

A(3, 5, 7),

B(4,1, 2),

E( 2, 0, 1),

i 2,

j 3;

3)

A( 3, 5,1),

B(6, 5, 3),

E(4, 1, 2),

i 1,

j 4;

4)

A(5, 3, 1),

B(2, 4, 7),

E(0, 1,1),

i 1,

j 3;

5)

A(5,8, 3),

B(4,1, 6),

E(1, 2, 3),

i 2,

j 4;

6)

A(7, 0, 4),

B(2, 5, 3),

E( 2, 6, 1),

i 2,

j 3;

7)

A(5, 3, 2),

B(1, 9, 4),

E( 4, 0, 5),

i 1,

j 4;

8)

A( 3,1,8),

B(1, 2, 4),

E(0, 3, 1),

i 3,

j 4;

9)

A(6, 1, 3),

B(2, 0, 5),

E(7, 2, 4),

i 1,

j 2;

10)

A(7, 2, 1),

B(3, 5, 4),

E(5,1, 0),

i 1,

j 3.

5

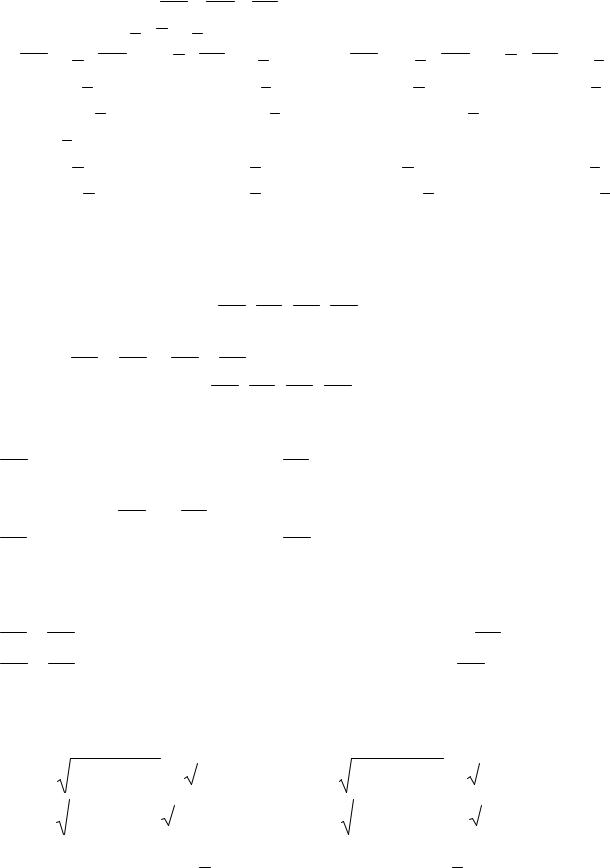
1.5. Векторы AB, BС, СA служат сторонами треугольника ABC.

Выразить через a, b и c векторы, совпадающие с медианами треугольника:

1)

AB

a

, BС 2b , СA 3

c

;

2)

AB

a

, BС 2b , СA

c

;

AB

3

a

BС

2

c

AB

2

a

BС

3

,

c

;

3)

,

b

,

СA

;

4)

,

b

СA

AB

2

a

BС

3

,

2

c

;

AB

3

a

,

BС

2

,

5)

,

b

СA

6)

b

СA

c

;

7)

AB

a

,

BС

,

СA

2

c

;

8)

AB

a

,

BС

2

,

СA

2

c

;

b

b

9)

AB

4

a

,

BС

,

СA

c

;

10)

AB

2

a

,

BС

,

СA

3

c

.

b

b

§1.3 Решение типового задания.

1.1.Даны координаты точек A(4, 2) и B( 1, 3). Вычислить:

1)координаты векторов AB, BA, OA, OB, где точка O– точка начала координат;

2)найти OA OB и OB OA сравнить результаты с п.1;

3)найти модули векторов AB, BA, OA, OB.

Решение:

1) Вычислим координаты векторов используя формулу (1.1)

AB ( 1 4;3 2) ( 5;1),

BA (4 ( 1); 2 3) (5; 1).

Вывод: противоположно направленные векторы отличаются знаком своих

координат т.е. AB BA
OA (4 0; 2 0) (4; 2),	OB ( 1 0; 3 0) ( 1, 3).

Вывод: координаты радиус-вектора точки совпадают с координатами самой точки.

2) Найдем разность векторов, используя формулу (1.5)

OA OB (4; 2) ( 1, 3) (4 ( 1); 2 3) (5; 1) BA;

OB OA ( 1; 3) (4; 2) ( 1 4;3 2) ( 5;1) AB.

Вывод: разность радиус-векторов точек дает координаты вектора противоположно направленного вектору построенному на этих точках.

3) Вычислим модули векторов по формуле (1.2):

		AB				( 5)2 12				26		,		BA		52 ( 1)2							26			;
																									.
						42 22													( 1)2 32
		ОА						20			,			ОВ										10
Вывод: модули противоположных векторов равны.
					1.2. Даны векторы					a	(1; 1;			0),				(3; 2; 1),			c	(4; 5;1).
																	b
Вычислить:

6

1) координаты и модуль векторов d 2a 4b , f a 3b 2c записать

векторы d и f линейной комбинацией базисных векторов;

2)векторы a и b являются сторонами параллелограмма. Найти длину его диагоналей (использовать действия сложения и вычитания векторов (Рис

1.2));

3)найти направляющие косинусы вектора c.

Решение:

1) Вектора d и f заданы линейной комбинацией векторов a и b , которые в свою очередь заданы координатами. Подставим в линейные комбинации заданные координаты:

d 2a 4b 2 (1; 1; 0) 4 (3; 2; 1) (2; 2; 0) (12;8; 4)(2 12; 2 8; 0 ( 4)) (14; 6; 4).

Мы нашли координаты вектора d , запишем его линейной комбинацией базисных векторов декартовой системы координат:

d (14; 6; 4) 14i 6j 4k .

Найдем его модуль: d 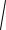142 62 ( 4)2 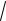248.

Аналогично вычисляем координаты и модуль вектора f

f a 3b 2c (1; 1; 0) 3 (3; 2; 1) 2 (4; 5;1)

( 1;1; 0) (9; 6; 3) (8;10; 2)

( 1 9 8;1 6 10; 0 ( 3) 2) (0; 3; 5);

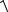
f a 3b 2c (0; 3; 5) 3j 5k ; f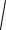( 3)2 ( 5)2 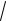34.

2) Для определения длины диагоналей, найдем координаты векторов,

их представляющих (рис. 1.5). Диагональ AC представляет из себя сумму

векторов a и b . Диагональ BD - разность этих векторов.

B C

a b

b

a

b

A D a

Рис. 1.5

AC a b (1 3; 1 2; 0 ( 1)) (4;1; 1);

AC 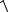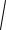42 12 ( 1)2 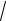18;

BD a b (1 3; 1 2; 0 ( 1)) ( 2; 3;1);

BD 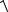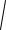( 2)2 ( 3)2 12 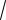14.

7

3) Для определения направляющих косинусов вектора c используем формулу (1.7)

cos	cx				,		cos				cy								,				cos								cz					.
		c											c																				c
								c				с										42		52					12													.
Вычислим модуль вектора									:																														42
Тогда, cos					4		, cos				5									, cos									1				.
					42						42																42
Проверка: cos2 cos2 cos2																							4							2								5 2
																									42													42

		1				2
						1.
		42

1.3. Вектор AB составляет с координатными осями Ox,Oy,Oz углы

, , соответственно. Вычислить координаты вектора AB, если: 600,

300, AB 5.

Решение:

Найдем координаты вектора AB (x, y, z), используя направляющие косинусы. Нам известно, что:

		x							y					0		1
cos					,	cos							cos60				,
																2
		AB							AB

cos

z

cos300

3

;

2

AB

Определим

значение cos :

1

1

3

0;

cos

1 cos2 cos2

4

4

1

5

x

cos 5 0 0,

y

cos 5

AB

AB

;

5

.

2

2

z

cos

5

3

3

AB

2

2

A(2,1, 3) и

B( 1, 0,1)

1.4.

Даны две

вершины

параллелограмма

ABCD и точка пересечения его диагоналей E(1, 1, 2). Найти:

1) координаты остальных вершин;

A

B,

2)

отрезок,

ограниченный

точками

и

разделен точками

M1, M2, M3, M4

на

пять

равных

частей.

Найти

координаты точек

Mi, M j, если

i 1,

j 4.

8

Решение:

1) Точка пересечения диагоналей, делит последнюю пополам (см. рис.1.5). Используем формулу деления отрезка пополам. Тогда для диагонали

AC имеем x	E		xA xC	, откуда	x	2x	E	x	A	. Для диагонали
		2			C

BD: xE xB xD , откуда xD 2xE xB.
2
Аналогичные формулы получаем для координат yи z точек Cи D.
xC 2 1 2 0,	yC 2 ( 1) 1 3,	zC 2 2 3 1;
xD 2 1 ( 1) 1,	yD 2 ( 1) 0 2,	zD 2 2 1 3.

Таким образом, вершины C и D имеют координаты: C (0, 3,1) и

D(1, 2, 3).

2)Точка M1 делит отрезок AB в отношении один к четырем (рис. 1.6), т.е.

AM1		1	,		1,		4. Точка M		делит отрезок AB в отношении
M1B 4				1		1		4

четыре к одному т.е. AM4 4, 2 4, 2 1.

M4B 1

M3 M4

B

M2

M1

A

Рис. 1.6

Используя формулу деления отрезка в данном отношении (1.8), получим координаты искомых точек:

x	M1					1xA 1xB							4 2 1 ( 1)												7		;
								1 1								4 1			5
y	M1						1yA 1yB							4 1 1 0					4				;
								1 1								4 1			5
z		M1						1zA 1zB							4 3 1 1						13			,					M	1	(	7	,	4	,	13	).
								1 1								4 1			5												5 5 5
x	M4						2xA 2xB									1 2 4 ( 1)										2		;
								2 2								1 4			5

9

y		M4			2 yA 2 yB							1 1 4 0								1		;
					2 2							1 4						5
z	M4			2zA 2zB							1 3 4 1								7		,		M	4	(	2	,	1	,	7	)
					2 2							1 4						5							5 5				5
			1.5. Векторы										,					служат сторонами треугольника ABC.
						AB			,			BС		СA

Выразить через a, b и c векторы, совпадающие с медианами треугольника:

AB 2a , BС b , СA 3c ;

Решение:

Воспользуемся свойством медианы: делит противолежащую сторону

пополам и правилом «замыкания ломанной». Выразим медиану AM линейной комбинацией известных векторов. Для этого необходимо выйти из точки A и прийти в точку M по сторонам треугольника (Рис. 1.7):

B

P M

A N C

Рис. 1.7

Т.е. AM AB BM AB 1 BC 2a 1( b) 2a 1b .

																											2						1	2												1	2														1
	Или																																					3			с						(						) 3					с								.
					AM							AС							СM									СA							BC
																																																		b														b
	Аналогично:																										2							2													2
													1														1		3																											2				a					1		3	c	;
		BN					BC								CA								b								c	,							BN						BA						AN
																											2
	2																																														2
		CP				CA						AP				3				c				a		,										CP				CB				BP												a	.
																																																					b

10