Подготовка по физике

(5.4.3)

В данном случае, согласно (5.4.2), – мнимое число, где

Можно показать, что A1 = 1, B3 = 0, тогда, учитывая значение q,получим решение уравнения Шредингера для трех областей в следующем виде:

(5.4.4)

В области 2 функция (5.4.4) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени не мнимые, а действительные.

Качественный анализ функций Ψ1(x), Ψ2(x), Ψ3(x) показан на рис. 5.4. Из рисунка следует, что

волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой.

Таким образом, квантовая механика приводит к принципиально новому квантовому явлению

– туннельному эффекту, в результате которого микрообъект может пройти через барьер.

Коэффициент прозрачности для барьера прямоугольной формы .

Для барьера произвольной формы .

Прохождение частицы сквозь барьер можно пояснить соотношением неопределенностей.

Неопределенность импульса на отрезке x = l

составляет

Связанная с этим

разбросом кинетическая энергия может оказаться достаточной для того, чтобы полная энергия оказалась больше потенциальной и частица может пройти через барьер.

С классической точки зрения прохождение частицы сквозь потенциальный барьер при E < U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом.

Строгое квантово-механическое решение задачи о гармоническом осцилляторе приводит еще к одному существенному отличию от классического рассмотрения. Оказывается, что можно

обнаружить частицу за пределами дозволенной области (рис. 5.5), т.е. за точками 0 и l(рис. 5.1).

Рис. 5.5

Это означает, что частица может прибывать там, где ее полная энергия меньше потенциальной энергии. Это оказывается возможным вследствие туннельного эффекта.

7. Гармонический осциллятор в квантовой механике.

Как известно, гармоническим осциллятором называется система, способная совершать гармонические колебания. В физике модель гармонического осциллятора играет важную роль, особенно при исследовании малых колебаний систем около положения устойчивого равновесия. Примером таких колебаний в квантовой механике являются колебания атомов в твердых телах, молекулах и т.д.

Рассмотрим одномерный гармонический осциллятор, совершающий колебания вдоль оси

под действием возвращающей квазиупругой силы . Потенциальная энергия такого осциллятора имеет вид

(4.77)

где - собственная частота классического гармонического осциллятора. Таким образом, квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы в параболической потенциальной яме (4.77) .

Рассмотрим сначала поведение классического гармонического осциллятора. Пусть частица с полной энергией совершает колебания в силовом поле (4.77) (рис.4.24). Точки и , в

которых полная энергия частицы равна потенциальной энергии , являются для частицы точками поворота. Частица совершает колебательные движения между стенками

потенциальной ямы внутри отрезка , выйти за пределы которого она не может.

Амплитуда колебаний определяется выражением .

Рис. 4.24.

В квантовой механике для решения задачи о гармоническом осцилляторе нужно решить уравнение Шредингера (4.6) с потенциальной энергией (4.77)

(4.78)

Вводя величины

(4.79)

и переходя к новой безразмерной переменной , приводим уравнение (4.78) к виду

(4.80)

Анализ показывает, что волновые функции, являющиеся решением уравнения (4.80) , будут непрерывными и конечными не при всех значениях параметра , а лишь при

Выражая, согласно (4.79), энергию осциллятора

через , получаем

(4.81)

Это соотношение и определяет закон квантования энергии гармонического осциллятора. Отметим, что энергетические уровни гармонического осциллятора, в отличие, например, от случая прямоугольной потенциальной ямы, являются эквидистантными, т.е. расположены на

одинаковом энергетическом расстоянии друг от друга (рис.4.25) .

Рис. 4.25.

Еще одной важной особенностью спектра (4.81) является наличие так называемых нулевых

колебаний - колебаний с энергией , соответствующих значению квантового числа

.

8.Водородоподобные атомы. Квантование энергии, вырожденность состояний по энергии, четыре квантовых числа (полный набор). Спектр излучения. Принцип Паули.

Водородоподобный атом — атом, содержащий в электронной оболочке один и только один электрон.

Таким атомом, кроме водорода и его тяжѐлых изотопов (дейтерия и трития), может быть любой ион, если число потерянных им электронов равно заряду атома - 1. Поскольку у такого иона остаѐтся только один электрон, его и называют водородоподобным атомом. Электронные спектры таких атомов описываются теорией Бора.

Как следует из решения уравнения Шредингера для атома водорода, квантовое состояние электрона в этом атоме (можно сказать и квантовое состояние атома) полностью определяется заданием трех квантовых чисел. "Задайте значения квантовых чисел, и я полностью опишу свойства атома" - так может современный физик перефразировать известное изречение Архимеда.

Каждое из квантовых чисел принимает только целочисленные значения и определяет, то есть предсказывает результаты измерения основных физических величин в заданном квантовом состоянии атома.

1.Главное квантовое число . Это квантовое число принимает значения

иопределяет полную энергию электрона в любом квантовом состоянии

(5.37)

.

Можно отметить, что эти значения энергии являются собственными значениями гамильтониана (5.17a). Поэтому в связанном состоянии электрон в атоме водорода имеет дискретный энергетический спектр, лежащий в области отрицательных значений и имеющий точку сгущения .

2. Орбитальное (азимутальное) квантовое число . В квантовых состояниях с заданным значением главного квантового числа азимутальное квантовое число может иметь следующие значения:

.

Из выводов предыдущего параграфа следует, что стационарные волновые функции , описывающие различные квантовые состояния атома, являются

собственными функциями не только оператора полной энергии , но и оператора квадрата момента импульса 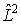, причем

.

Следовательно, в любом квантовом состоянии атом обладает определенным значением квадрата момента импульса, причем модуль орбитального момента импульса движущегося в атоме электрона однозначно определяется орбитальным квантовым числом:

	.	(5.38)
Проанализируем эту формулу	квантования момента импульса. Сравнивая ее с
условием (5.3) квантования момента	импульса движущегося электрона в теории Бора, можно

заметить, что эти условия не совпадают. И дело не только в отличии числовых значений, рассчитанных по этим формулам. Принципиальное отличие этих соотношений состоит в том, что в

квантовой	механике	возможны	состояния атома с нулевым моментом импульса.				Во всех	-
состояниях	и,	частности,		в	основном -состоянии,	когда	,	по
формуле (5.38) получаем			.

При классическом описании движения электрона в атоме по определенной траектории (орбите) в любом состоянии атом должен обладать ненулевым моментом импульса.

Опыт подтверждает существование квантовых состояний атома с нулевыми орбитальными моментами. Следовательно, опыт подтверждает, что только отказ от классического траекторного способа описания движения электрона в атоме позволяет правильно рассчитать и предсказать свойства атома. Вероятностный способ описания движения частиц в квантовой механике является единственно правильным способом описания свойств атомных систем - таков вывод современной физики.

Так как движущийся вокруг ядра электрон является заряженной частицей, то такое движение обуславливает протекание некоторого замкнутого тока в атоме, который можно

охарактеризоватьорбитальным магнитным моментом .

В теории Бора, когда с позиции классической теории рассматривается круговое движение электрона по орбите радиуса со скоростью , величина орбитального механического момента

равна	. Если время полного оборота электрона	, то такому движению соответствует
замкнутый ток

,

который можно охарактеризовать величиной магнитного момента

.

Связь механического и магнитного моментов при этом определяется гиромагнитным отношением

(5.39)

.

Так как заряд электрона отрицателен, то для орбитального движения направление вектора

магнитного	момента	противоположно направлению вектора механического момента
импульса	(рис. 5.8).

Для расчета орбитального магнитного момента в квантовой теории следует определить пространственную плотность электрического тока через плотность потока вероятностей по

формуле: . Плотность потока вероятности при этом можно найти по формуле (3.23), зная волновую функцию электрона в заданном квантовом состоянии атома. Точный квантовомеханический расчет гиромагнитного отношения также приводит к формуле (5.39).

Рис. 5.8.

Итак, в любом квантовом состоянии атом водорода обладает не только механическим моментом , величина которого определяется формулой (5.38), но и магнитным моментом.

(5.40)

.

Здесь универсальная постоянная

служит единицей измерения магнитных моментов атомов и называется магнетоном Бора. Если атом переходит из одного квантового состояния в другое с испусканием (поглощением)

фотона излучения, то возможны лишь такие переходы, для которых орбитальное квантовое

число изменяется	на единицу. Это правило, согласно которому для оптических
переходов	, называется правилом отбора. Наличие такого правила отбора обусловлено

тем, что электромагнитное излучение (фотон) уносит или вносит не только квант энергии, но и вполне определенный момент импульса, изменяющий орбитальное квантовое число для

электрона всегда на единицу.
3. Магнитное квантовое			число	. В квантовом состоянии с заданным		значением
орбитального	квантового	числа	, магнитное квантовое число может		принимать
различных значений из ряда
				.
Физический смысл		магнитного		квантового числа вытекает из того, что		волновая
функция	,	описывающая		квантовое состояние электрона	в атоме	водорода,

является собственной функцией оператора проекции момента импульса , причем

.

Поэтому, из общих положений квантовой механики (см. раздел 3.5) следует, что проекция момента импульса электрона на выделенное в пространстве направление может иметь только определенные значения, равные

.	(5.41)

Направление в пространстве обычно выделяется внешним полем (например, магнитным или электрическим), в котором находится атом.

Так как формула (5.41) квантования проекции механического момента соответствует вполне

определенным направлениям ориентации в пространстве вектора (рис. 5.9), то эту формулу называют обычно формулой пространственного квантования.

Сточки зрения классического представления об электронной орбите, с учетом

перпендикулярности вектора к плоскости орбиты, соотношение (5.41) определяет возможные дискретные расположения электронных орбит в пространстве по отношению к направлению внешнего поля.

Рис. 5.9.
Отмеченная выше связь механического и магнитного	моментов	атома позволяет	с
учетом (5.41) записать также возможные значения проекции	магнитного	момента атома	на
выделенное направление :
,		(5.42)

зависящие от значения магнитного квантового числа .

Принцип Паули. В одном и том же атоме (или в какой-либо другой квантовой системе) не может быть двух электронов (либо других частиц с полуцелым спином), обладающих одинаковым набором квантовых чисел.