02_Сущность методов

Лекция №5. Сущность экономико-математических методов¹

Методы

Особенностью решения задач проектирования является необходимость учета множества переменных величин, характеризующих внешние условия (грунты, климат, интенсивность и т.п.). Число сочетаний этих величин может быть достаточно большим, тогда возможно существование значительного числа вариантов решений. И тем не менее необходимо получить оптимальное или близкое к нему решение. Поэтому требуются специальные методы, позволяющие в приемлемые сроки с достаточной степенью обоснованности, с учетом особенностей дорожной отрасли, выйти на искомое решение.

В процессе решения прикладных задач приходится формализовать зависимость между отдельными элементами экономической системы, применять математический аппарат, общие кибернетические² закономерности и принципы, т.е. использовать ЭММе.

По характеру используемого математического аппарата можно выделить методы классической и прикладной математики.

Методы классической математики включают математический анализ (дифференциальное и вариационное исчисления) и теорию вероятностей. Эти методы целесообразно использовать при расчете параметров календарно-плановых нормативов - определение объемов поставляемых материалов, длительности производственного цикла, величины заделов, а также при решении задач оперативного регулирования хода строительства и т.д.

Методы прикладной математики можно классифицировать следующим образом:

• методы оптимального программирования;

• методы математической статистики;

• комбинаторные методы;

• теория расписаний;

• теория игр и др.

Оптимальное программирование - это комплекс специальных методов, обеспечивающих в условиях множества возможных решений выбор такого, которое является наилучшим (оптимальным) по заданному критерию при определенных ограничительных условиях. В их числе линейное, нелинейное, стохастическое, выпуклое, квадратичное, параметрическое, блочное, целочисленное (дискретное), динамическое программирование и др. В математике, решаемые на оптимум задачи называются экстремальными, в них требуется отыскать максимум или минимум некоторой целевой функции.

Линейное программирование используется при решении задач в том случае, когда целевая функция и ограничительные условия выражены линейными зависимостями. Отыскиваемые при этом неизвестные переменные обеспечивают экстремум целевой функции (расчет балок мостов по линиям влияния, оптимизация расположения грунтовых карьеров и передвижных АБЗ).

Методы нелинейного программирования используются тогда, когда зависимости между переменными носят нелинейный характер. Задачи нелинейного программирования достаточно сложны, т.к. нет универсального метода их реализации.

Стохастическое программирование - если в системе равенств или неравенств (ограничений) содержатся случайные элементы, но зависимости между переменными – линейные.

Выпуклое программирование представляет собой совокупность специальных методов решения нелинейных экстремальных задач, у которых выпуклы либо целевые функции либо ограничительные условия.

Квадратичное программирование – это совокупность методов решения особого класса экстремальных задач, в которых ограничительные условия линейны, а целевая функция является многочленом второй степени.

Целочисленное (дискретное) программирование – если при нахождении неизвестных переменных необходимо чтобы одна из них или несколько принимали только целочисленные значения. В терминах дискретного программирования формализуются многие важные задачи экономики, управления, планирования, проектирования, а также ряд других задач.

Методы динамического программирования могут применяться для решения таких оптимизационных задач, в которых необходимо рассматривать процесс производства или управления в пространстве или во времени, т.е. в развитии. При этом процедура вычислений реализуется по своеобразной схеме: весь процесс поиска оптимального решения представляется в виде определенной последовательности шагов, для каждого из которых находится оптимальное решение, причем оптимальность определяется влиянием на последующие шаги. Сам процесс поиска решения на базе рассматриваемых методов является многошаговым. При этом ода задача со множеством переменных заменяется многими задачами с небольшим (даже одной) числом переменных.

Ограничительные условия применения указанных методов следующие: итоговый оптимум является суммой оптимальных решений каждого из выделенных шагов, а состояние системы в рассматриваемый момент времени определяет выбор оптимального решения , причем, на выбор этого решения оказывают влияние состояния системы в предшествующие моменты.

Модели, содержащие большое число показателей, очень сложны в реализации, поэтому в тех случаях, когда это возможно, их преобразуют в несколько моделей меньшей размерности, тем самым разлагают задачу. Полученные локальные задачи решаются совместно по специальным правилам. Методы, позволяющие решать задачи в рассматриваемом порядке, относятся к методам блочного программирования (расчет дорожной одежды).

Методы математической статистики используют для нахождения и раскрытия свойственных большим, совокупностям однородных объектов, закономерностей. Полученные характеристики такой выборки могут использоваться для сравнительной оценки элементов различных совокупностей или их характеристик, а также для установления связи между отдельными величинами и программирования на этой основе развития системы в будущем (прогнозирование). При этом изучается не каждый элемент совокупности, а определенная выборка. Математическая статистика включает: корреляционны, регрессионный, дисперсионный, факторный анализ и др. Эти методы используются при расчете параметров нормативов, в анализе производственно-хозяйственной деятельности предприятий, при решении задач управления запасами, массового обслуживания.

Комбинаторные методы используются для решения задач, которые не могут быть реализованы классическими методами математического программирования, например: ветвей и границ. Сюда близко подходят эвристические методы, основанные на опыте, интуиции исполнителя (проектировщика).

Теория расписаний позволяет решать такие задачи как закрепление деталей за оборудованием во времени, сбалансированность работы АБЗ, асфальто- и бетоноукладчиков и др., т.е. задачи повременного (календарного) планирования производства. При их решении кроме соответствующего критерия качества расписания, необходимо выполнить требование соблюдения определенных технологических условий. Подобные методы дают оптимальное (дискретное и динамическое программирование) или приближенное решение (эвристическое или случайного поиска).

Методы теории игр применяются, когда приходится принимать решение в условиях неопределенности, причем такое решение должно обеспечивать наибольший эффект или наименьшие потери.

Симплексный метод на основе полных таблиц

Симплексный метод – один из методов линейного программирования. В его основе лежит с некоторыми дополнениями метод последовательных исключений, представляющий собой совокупность удобных вычислительных алгоритмов, построенных на последовательном применении тождественных (симплексных) преобразований системы линейных уравнений.

Одной из задач решаемых симплексным методом является задача об определении оптимального ассортимента продукции. Предприятие может производить n видов изделий a₁, a₂, …, a_n располагая для их изготовления ограниченными ресурсами b₁, b₂, …, b_m. Данные, представленные в табл. 1, характеризуют затраты каждого вида ресурса на изготовление одного изделия.

Таблица 1

Виды ресурсов	Объем ресурсов	Затраты на одно изделие
		a1	a2	…	an
b1	B1	C11	C12	…	C1n
b2	B2	C21	C22	…	C2n
…	…	…	…	…	…
bm	Bm	Cm1	Cm2	…	Cmn
Прибыль в руб.		П1	П2	…	Пn

Требуется определить сколько изделий a₁, a₂, …, a_n должно производить предприятие, чтобы достичь наибольшей прибыли.

Введем искомые неизвестные х₁, х₂, …, х_n обозначающие число изделий a₁, a₂, …, a_n, которые должно производить предприятие.

Тогда математически задачу можно сформулировать следующим образом.

Среди множества неотрицательных решений системы неравенств

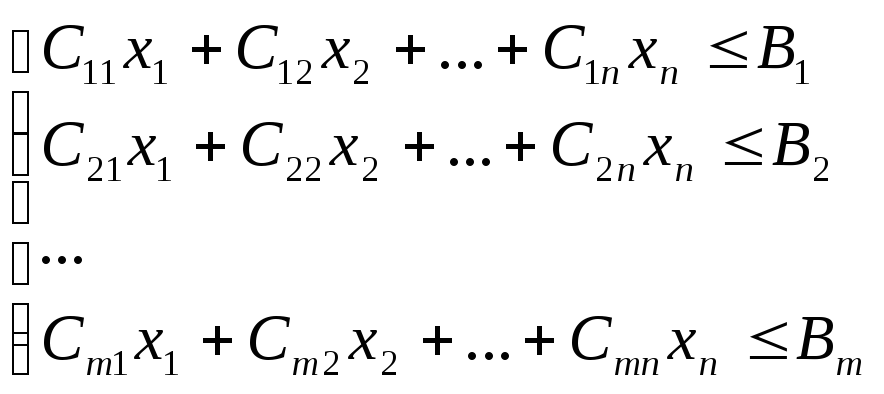
найти такое решение, для которого целевая функция

Z = П₁x₁ + П₂x₂ + … +П_nx_n

достигает наибольшего значения.

П Р А К Т И К А № 5

Рассмотрим геометрическое решение задачи на примере предприятия, которое может производить два вида изделий А и В, располагая ограниченными ресурсами материала чугуна и стали соответственно в количествах 350 и 392 кг и оборудования в количестве 408 станко-часов.

Таблица 2

Виды ресурсов	Объем ресурсов	Затраты на одно изделие
		А	В
Чугун	350	14	5
Сталь	392	14	8
Оборудование	408	6	12
Прибыль в руб.		10	5

Искомые неизвестные x₁ и х₂, обозначают число изделий А и В, которые должно производить предприятие.

(1)

найти такое решение, для которого функция

Z = 10х₁ + 5х₂ (2)

достигает наибольшего значения.

Построим область допустимых решений, соответствующую системе неравенств (1). Для этого, заменив каждое из неравенств равенством

14x₁ + 5х₂ = 350, (1-я прямая),

14x₁ + 8х₂ = 392, (2-я прямая),

6x₁ + 12х₂ = 408, (3-я прямая),

строим граничную линию. Учитывая, что x₁ > 0 и х₂ > 0, получаем заштрихованную часть плоскости, образующую многоугольник решений OABCD.

Рис. 2.1

Затем строим линию уровня 10х₁ + 5х₂ = 0 и вектор (10;5), которые взаимно перпендикулярны. Нетрудно показать, что вектор дает направление наибольшего возрастания линейной функции.

Действительно

Z₀ = 10х₁₀ + 5х₂₀ = 10  0 + 5  0 = 0,

Z_A = 10х_1А + 5х_2А = 10  0 + 5  34 = 170,

Z_D = 10х_1D + 5x_2D = 10  25 + 5  0 = 250 и т. д.

Из всех линий уровня выбираем две, из которых одна проходит через точку 0 и дает min значение функции Z, a другая проходит через точку С и функция Z для нее принимает max значение. Эти линии уровня называются опорными.

Точка С образована первой и второй прямыми. Следовательно, решая систему уравнений

,

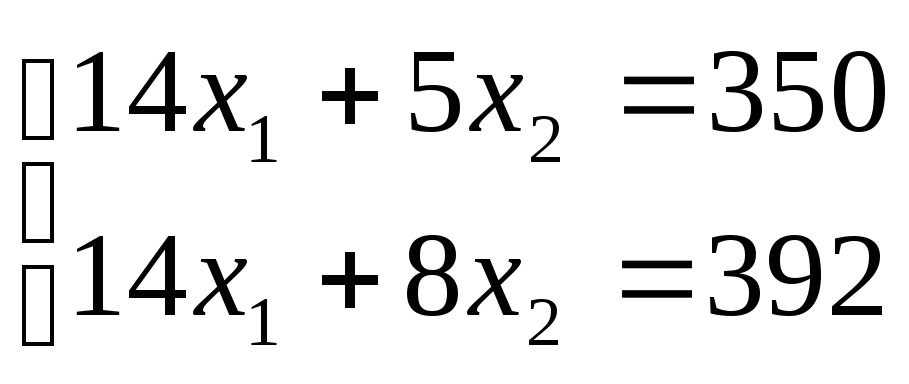найдем координаты точки С

x₁ = 20, х₂ = 14,

при этом Z_max = 10  20 + 5  14 = 270 руб.

Таким образом, max прибыль в 270 руб. будет получена, если предприятие произведет 20 изделий вида А и 14 изделий вида В.

Лекция №6 Транспортная задача.

Это задача о наиболее экономном плане перевозок однородного или взаимозаменяемого продукта из пунктов производства (станций отправления) в пункты потребления (станции назначения).

Транспортная задача является важнейшей частной моделью линейного программирования, имеющей обширные практические приложения не только к проблемам транспорта. Особо важное значение она имеет в деле рационализации поставок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта.

Постановка задачи и ее математическая модель

Некоторый однородный продукт производится в m пунктах производства А₁, А₂, ..., А_т. Задан объем производства a_i пункта A_i(). Произведенный продукт должен быть перевезен в n пунктов_потребления В₁ В₂, ..., В_n. Известен спрос b_j. пункта В_j () Заданы также транспортные издержки C_ij, связанные с перевозкой единицы продукта из пункта А_i в пункт В_j. Требуется составить план перевозок, обеспечивающий при минимальных транспортных расходах (издержках) удовлетворения спроса всех пунктов потребления за счет продукта, произведенного во всех пунктах производства.

Обозначим через x_ij количество единиц груза, запланированных к перевозке от i-го поставщика к j-му потребителю. Тогда условие задачи можно записать в виде табл. 1, которую в дальнейшем будем называть матрицей планирования.

Таблица 1

Поставщики	Потребители								Запасы
	В1		…	Bj		…	Bn
а1		С11	…		С1j	…		С1n	a1
	xl1			xlj			xln
…	…		…	…		…	….		…
Ai		Сi1	…		Сij	…		Сin	ai
	xi1			xij			xin
…	…		…	…		…	...		…
Am		Сm1	…		Сmj	…		Сmn	am
	xm1			xmj			xmn
Потребности	b1		…	bj		…	bn		∑ai ∑bj

Тогда математическая формулировка транспортной задачи сводится к минимизации линейной формы

при ограничениях

,

(ограничения по запасам),

,

(ограничения по потребностям),

x_ij ≥ 0

Различают задачи с закрытой моделью, когда ∑a_i=∑b_j и открытой моделью, когда ∑a_i≠∑b_j т.е. баланс между запасами и потребностями отсутствует.

Необходимым и достаточным условием разрешимости транспортной задачи является равенство суммарных запасов суммарным потребностям, т.е. .

Если ∑a_i>∑b_j, то вводят фиктивный (n + 1)-й пункт назначения с потребностью b_n+1 = ∑a_i-∑b_j и полагают c_i,n+1=0, .

Если ∑a_i<∑b_j, то вводят фиктивный (m + 1)-й пункт отправления с запасами a_m+1 = ∑b_j-∑a_i и полагают c_m+1,j=0, .

Самым распространенным методом решения транспортной задачи является метод потенциалов. Решение разбивается на два этапа:

1. Определение начального допустимого базисного решения (первого опорного плана) - первоначальное распределение поставок.

2. Построение последовательных итераций (шагов), улучшающих опорные планы (каждый новый план не должен увеличивать суммарные затраты).

После выполнения первого этапа шаги второго этапа проводятся до тех пор, пока не будет найдено оптимальное распределение поставок.

Построение первоначального опорного плана

Рассмотрим два метода построения первого опорного плана.

План составляется последовательным заполнением по одной клетке в таблице перевозок так, что каждый раз либо полностью удовлетворяется потребность одного из потребителей, либо полностью вывозится груз от некоторого поставщика. Различие двух методов отыскания первого опорного плана состоит в различии способов выбора последовательности заполнения клеток.

Диагональный метод или метод северо-западного угла. При этом методе на каждом шаге построения первого опорного плана заполняется верхняя левая клетка ("северо-западный угол") оставшейся части таблицы. При таком методе заполнение таблицы начинается с клетки переменного х₁₁ и заканчивается в клетке неизвестного x_mn, т. е. идет как бы по диагонали таблицы перевозок.

Метод наименьшей стоимости. Исходное опорное решение, построенное диагональным методом, как правило, оказывается весьма далеким от оптимального, так как при его определении совершенно игнорируются величины затрат с_ij. Поэтому требуются в дальнейших расчетах много итерации для достижения оптимального плана. Число итераций можно сократить, если исходный план строить по более рациональному правилу "минимального элемента". Сущность его состоит в том, что на каждом шаге заполняется клетка с наименьшей величиной с_ij. Если такая клетка не единственная, то лучше заполнять ту, по вертикали или горизонтали которой встречаются большие c_ij, а в принципе заполняется любая из них. Необходимо отметить, что при наличии в таблице клеток с одинаковыми тарифами, планы, полученные с помощью этого метода, могут быть разными, однако они, несомненно, ближе к оптимальному, чем план, составленный по методу северо-западного угла.

Условие закрытости модели транспортной задачи означает, что среди m+n уравнений системы ограничений независимых только m+n-1, поэтому в любом базисном решении этой системы должно быть m+n-1 базисных переменных. Поскольку свободные переменные в таком решении равны нулю, то в транспортной таблице им будут соответствовать пустые клети.

Клетки таблицы, в которых записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) — свободными.

План называется вырожденным, если количество базисных клеток в нем меньше, чем m+n-1.

Если на каком-то этапе решения получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток 0 и тем самым объявив их базисными. Поскольку этим дополнительным клеткам будут отвечать нулевые перевозки, то общий баланс и суммарная стоимость перевозок плана при этом не изменится. Однако проводить пополнение плана, выбирая клетки произвольно, нельзя. Приведем условия, которым должен соответствовать пополненный план.

Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ломаная может иметь точки самопересечения, но не в клетках цикла.

План называется ациклическим, если его базисные клетки не содержат циклов.

Доказано, что оптимальные планы являются ациклическими, поэтому и первоначальный план также должен удовлетворять этому требованию. Заметим, что планы, полученные с помощью методов северо-западного угла и наименьшей стоимости, ациклические. Однако если план оказался вырожденным, то при его пополнении требование ацикличности необходимо учитывать.

Оптимальность базисного решения. Метод потенциалов

Получив первый опорный план, следует проверить его оптимальность и, если требуется, перейти к новому опорному плану с лучшим значением целевой функции Z. Для этого применяют метод потенциалов. Каждому поставщику А_i и каждому потребителю В_j. сопоставляют, соответственно, величины U_i и V_j — потенциалы этих пунктов.

Для того чтобы некоторый опорный план транспортной задачи был оптимальным, необходимо и достаточно, чтобы ему соответствовала система из (m+n) чисел, удовлетворяющих условиям: