
Матлогики
.pdf
Высказывание — (термин из математической логики) это утверждение, которое является либо истинным, либо ложным. Логическое высказывание принято обозначать заглавнойлатинской буквой.
Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.
Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.
Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.
Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.
Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.
Теорема 2.2. Логическое значение составного высказывания  равно значению формулы
равно значению формулы  на наборе
на наборе  логических значений составляющих высказываний
логических значений составляющих высказываний  , т.е.
, т.е.
Доказательство. Докажем утверждение методом полной математической индукции по числу символов логических операций, входящих в формулу 
 .
.
Если формула 
 содержит 0 символов логических операций, то она представляет собой просто пропозициональную переменную, скажем,
содержит 0 символов логических операций, то она представляет собой просто пропозициональную переменную, скажем,  , т.е.
, т.е.
 (знак
(знак  обозначает абсолютную тождественность двух формул, графическую одинаковость левой и правой частей). Тогда доказываемое соотношение сводится к
обозначает абсолютную тождественность двух формул, графическую одинаковость левой и правой частей). Тогда доказываемое соотношение сводится к
тривиальному равенству:  .
.
Если формула  содержит лишь один символ логической операции, то она является одной из следующих формул:
содержит лишь один символ логической операции, то она является одной из следующих формул:

В этих случаях доказываемое равенство есть одно из равенств (1.1)–(1.5).
Предположим теперь, что утверждающееся в теореме равенство верно для всех формул алгебры высказываний, содержащих не более к символов логических операций. Докажем, что оно верно для
формулы  , содержащей
, содержащей  символов логических операций. На основании определения 2.1 формула
символов логических операций. На основании определения 2.1 формула  имеет один из следующих видов:
имеет один из следующих видов:
где  и
и  — некоторые формулы, каждая из которых содержит уже не более к символов логических операций. Нужно провести доказательство для всех пяти случаев. Но в силу принципиальной идентичности этих доказательств проделаем его, например, для случая
— некоторые формулы, каждая из которых содержит уже не более к символов логических операций. Нужно провести доказательство для всех пяти случаев. Но в силу принципиальной идентичности этих доказательств проделаем его, например, для случая
 . Вычисляем:
. Вычисляем:
В проделанных вычислениях второе равенство основано на определении 1.3 логической операции конъюнкции. Третье равенство основано на предположении индукции о том, что для формул  и
и  соотношение теоремы выполняется. Наконец четвертое равенство записано на основании того, что
соотношение теоремы выполняется. Наконец четвертое равенство записано на основании того, что
.
Аналогичным образом соотношение теоремы доказывается и во всех остальных случаях конструирования формулы  из формул
из формул  и
и  .
.
Следовательно, утверждение теоремы верно для любой формулы  алгебры высказываний.
алгебры высказываний.
Формула алгебры высказываний  называется выполнимой, если
называется выполнимой, если

некоторая ее конкретизация является истинным высказыванием, т.е. существуют такие конкретные высказывания  , которые, будучи подставленными в эту формулу вместо переменных
, которые, будучи подставленными в эту формулу вместо переменных  соответственно, превращают ее в истинное высказывание. Таким образом,
соответственно, превращают ее в истинное высказывание. Таким образом,  выполнима, если существуют такие конкретные высказывания
выполнима, если существуют такие конкретные высказывания
 , что
, что  . Выполнимой формулой является, в частности, формула, рассмотренная в примере 2.4. Она превращается в истинное высказывание,
. Выполнимой формулой является, в частности, формула, рассмотренная в примере 2.4. Она превращается в истинное высказывание,
если, например, вместо пропозициональных переменных  подставить ложные
подставить ложные
высказывания. Выполнима также формула  , конкретизация которой рассмотрена в начале этой лекции.
, конкретизация которой рассмотрена в начале этой лекции.
Формула 
 называется тавтологией, или тождественно истинной, если она превращается в истинное высказывание при всякой подстановке вместо переменных конкретных
называется тавтологией, или тождественно истинной, если она превращается в истинное высказывание при всякой подстановке вместо переменных конкретных
высказываний  , т.е. если
, т.е. если  для любых высказываний
для любых высказываний  . Формула из примера 2.3 является тавтологией. Для обозначения тавтологии используется знак
. Формула из примера 2.3 является тавтологией. Для обозначения тавтологии используется знак  , который ставится перед формулой, являющейся тавтологией. Таким образом, запись
, который ставится перед формулой, являющейся тавтологией. Таким образом, запись  означает, что формула
означает, что формула  является тавтологией. В частности, для указанного примера можем записать
является тавтологией. В частности, для указанного примера можем записать  .
.
Формула  называется опровержимой, если существуют такие конкретные высказывания
называется опровержимой, если существуют такие конкретные высказывания  , которые превращают данную формулу в ложное высказывание
, которые превращают данную формулу в ложное высказывание
 , т.е.
, т.е.  . Другими словами, опровержимые формулы
. Другими словами, опровержимые формулы
— это формулы, не являющиеся тавтологиями. Опровержимой является формула, рассмотренная в примере 2.4. Она обращается в ложное высказывание лишь тогда, когда вместо всех переменных

 подставлены истинные высказывания. Формула
подставлены истинные высказывания. Формула  также опровержима.
также опровержима.
Наконец, формула  называется тождественно ложной, или противоречием, если
называется тождественно ложной, или противоречием, если 
 для любых конкретных высказываний
для любых конкретных высказываний
 . Другими словами, тождественно ложные формулы — это такие формулы, которые не являются выполнимыми.
. Другими словами, тождественно ложные формулы — это такие формулы, которые не являются выполнимыми.
Правило заключения При выводе формулы из множества аксиом и посылок используют два основных правила:
а) если Fi и ( Fi ® Fj ) есть выводимые формулы, то Fj также выводимая формула, т.е.

Fi; (Fi®Fj)
Fj.
это правило называют modus ponens (m.p.).
b) если формулы ùFj и (Fi®Fj) есть выводимые формулы, то ùFi также выводимая формула, т.е
ùFj; (Fi®Fj)
ùFi.
это правило называют modus tollens (m.t.).
Правило подстановки: Если формула A доказуема в исчислении высказываний, x – переменная, B –
произвольная формула исчисления высказываний (и.в.), то формула, полученная в результате замены в формуле A переменной x формулой B, является также доказуемой формулой. Операция
замены в формуле Aпеременной x формулой B называется подстановкой и обозначается 
.
2. Правило заключения: Если формулы A и A→B доказуемы в исчислении высказываний, то формула B также доказуема.
Равносильные формулы алгебры логики
Определение. Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных).
Обозначение. A≡B.
Теорема 4.2 (признак равносильности формул). Две формулы 
 и
и  алгебры высказываний равносильны тогда и только тогда, когда формула
алгебры высказываний равносильны тогда и только тогда, когда формула  является тавтологией:
является тавтологией:
(4.2)
Доказательство. Если 
 , то по определению 4.1
, то по определению 4.1
для любых высказываний 
 . Тогда (по
. Тогда (по
определению 1.9 операции эквивалентности)  , откуда на основании соотношения (1.5) заключаем, что
, откуда на основании соотношения (1.5) заключаем, что

 для любых
для любых  . Последнее означает по определению тавтологии, что
. Последнее означает по определению тавтологии, что 
 . Обратными рассуждениями доказывается утверждение: если
. Обратными рассуждениями доказывается утверждение: если 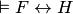 , то
, то  . Итак, теорема доказана.
. Итак, теорема доказана.
Отметим, что равносильность формул — это не (логическая) операция над формулами, а отношение между формулами логики высказываний. Это означает, что если  и
и  — формулы, то выражение
— формулы, то выражение  уже не является формулой алгебры высказываний; оно — утверждение о некотором взаимоотношении между формулами
уже не является формулой алгебры высказываний; оно — утверждение о некотором взаимоотношении между формулами  и
и  , лишь сокращенная (символическая) запись утверждения (высказывания) "
, лишь сокращенная (символическая) запись утверждения (высказывания) " равносильна
равносильна  " об этих формулах. Это утверждение либо истинно, либо ложно, т.е.
" об этих формулах. Это утверждение либо истинно, либо ложно, т.е.  и
и  либо находятся в отношении равносильности, либо нет. В приведенном далее следствии из теоремы 4.2 устанавливаются некоторые свойства этого отношения между формулами алгебры высказываний.
либо находятся в отношении равносильности, либо нет. В приведенном далее следствии из теоремы 4.2 устанавливаются некоторые свойства этого отношения между формулами алгебры высказываний.
Следствие 4.3. Отношение равносильности между формулами алгебры высказываний:
а) рефлексивно:  ;
;
б) симметрично: если  , то
, то  ;
;
в) транзитивно: если  и
и  , то
, то  , т.е. отношение равносильности является отношением эквивалентности.
, т.е. отношение равносильности является отношением эквивалентности.
Доказательство. Рефлексивность следует непосредственно из тавтологии теоремы 3.3, о и теоремы 4.2.
Для доказательства симметричности отношения  предположим, что
предположим, что  , т.е. на основании признака равносильности (теорема 4.2)
, т.е. на основании признака равносильности (теорема 4.2)  . Тогда по тавтологии теоремы 3.3,
. Тогда по тавтологии теоремы 3.3,
пункт п) заключаем: формула  принимает всегда те же самые значения, что и формула
принимает всегда те же самые значения, что и формула
 , т.е. только истинные значения. Следовательно,
, т.е. только истинные значения. Следовательно,  или (по признаку равносильности)
или (по признаку равносильности)  . Симметричность доказана.
. Симметричность доказана.
Наконец, если 
 и
и 
 , т.е.
, т.е.  и
и 
 , то на основании
, то на основании
определения конъюнкции заключаем, что:  . Привлекая теперь тавтологию из теоремы 3.3, пункт р) и правило заключения для получения тавтологий (теорема 3.5),
. Привлекая теперь тавтологию из теоремы 3.3, пункт р) и правило заключения для получения тавтологий (теорема 3.5),
получаем 
 , или (по теореме 4.2)
, или (по теореме 4.2)  . Следовательно, отношение
. Следовательно, отношение 
 транзитивно.
транзитивно.
Таким образом, отношение 
 есть отношение эквивалентности, что и требовалось доказать.
есть отношение эквивалентности, что и требовалось доказать.

Справедливы следующие равносильности:
Лемма 4.5 (о замене). Если 
 , то для любой формулы алгебры высказываний
, то для любой формулы алгебры высказываний 
 имеет место равносильность
имеет место равносильность
Другими словами, если в формуле некоторую ее подформулу заменить на равносильную ей формулу, то полученная формула будет равносильна исходной.
Доказательство. Поскольку формулы  и
и  принимают всегда одинаковые значения при одинаковых значениях пропозициональных переменных
принимают всегда одинаковые значения при одинаковых значениях пропозициональных переменных 
 , то формулы
, то формулы
и
принимают одинаковые значения при любых одинаковых наборах значений переменных  и
и 
 Следовательно,
Следовательно,
то есть
, что и требовалось доказать.
Например, на основании этой леммы и равносильности из теоремы 4.4 (пункт п), формула
 равносильна формуле
равносильна формуле  .
.

Общая формулировка леммы о замене может быть конкретизирована в соответствии с индуктивным определением формулы следующим образом. Пусть имеется формула  . Если
. Если
 , то
, то  . Далее, пусть исходная формула имеет следующее строение:
. Далее, пусть исходная формула имеет следующее строение: 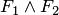 .
.
Если  , то
, то 
 . Если, кроме того,
. Если, кроме того,  , то
, то
, то есть  .
.
Об этом свойстве говорят, что отношение равносильности формул стабильно относительно операции конъюнкции. (Предыдущее свойство означает стабильность относительно отрицания.) Аналогично, отношение равносильности стабильно и относительно остальных логических операций — дизъюнкции, импликации и эквивалентности. Это означает, что если  и
и  , то
, то
Равносильные преобразования формул
Используя лемму о замене и приведенные в теореме 4.4 равносильности, можем от одной формулы переходить к равносильной ей формуле. Такой переход называется равносильным преобразованием исходной формулы. Равносильные преобразования формул применяются прежде всего для упрощения формул.
Пример 4.6. Упростим формулу  , используя равносильности из теоремы 4.4:
, используя равносильности из теоремы 4.4:
Равносильные преобразования формул применяются также для приведения формул к специальному виду или к специальной форме (к так называемой совершенной нормальной форме), имеющей исключительно важное значение как в самой алгебре высказываний, так и в ее приложениях. Об этом речь пойдет в следующей лекции.

Конъюнкти́вный одночле́н (минте́рм) от переменных  — конъюнкция этих переменных или[1] их отрицаний.
— конъюнкция этих переменных или[1] их отрицаний.
Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.
Конъюнкти́вная норма́льная фо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ.[1] Для этого можно использовать: закон двойного отрицания, закон де Моргана, дистрибутивность.
Соверше́нная конъюнкти́вная норма́льная фо́рма (СКНФ) — это такая КНФ, которая удовлетворяет трём условиям:
●в ней нет одинаковых элементарных дизъюнкций
●в каждой дизъюнкции нет одинаковых пропозициональных переменных
●каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
Соверше́нная дизъюнкти́вная норма́льная фо́рма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:
●в ней нет одинаковых элементарных конъюнкций
●в каждой конъюнкции нет одинаковых пропозициональных букв
●каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.
Для любой функции алгебры логики существует своя СДНФ, причём единственная.
Формула 
 называется логическим следствием формул
называется логическим следствием формул
 , если формула
, если формула  превращается в истинное высказывание при всякой такой подстановке вместо всех ее пропозициональных переменных
превращается в истинное высказывание при всякой такой подстановке вместо всех ее пропозициональных переменных  конкретных высказываний, при которой в истинное высказывание превращаются все формулы
конкретных высказываний, при которой в истинное высказывание превращаются все формулы  . То, что формула
. То, что формула  является логическим следствием формул
является логическим следствием формул  , записывается так:
, записывается так:  .
.
Формулы 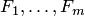 называются посылками для логического следствия
называются посылками для логического следствия  .
.
Таким образом,  , если для любых высказываний
, если для любых высказываний  из
из

 следует
следует
 .
.
Наконец можно и так сказать о логическом следствии. Составим таблицы истинности для формул
 . Предположим, что если в какойто строке таблицы все формулы
. Предположим, что если в какойто строке таблицы все формулы  принимают значение 1, то в этой строке непременно и формула
принимают значение 1, то в этой строке непременно и формула  принимает значение 1. Это и будет означать, что
принимает значение 1. Это и будет означать, что  является логическим следствием формул
является логическим следствием формул  .
.
Алгоритм проверки формул на логическое следование
Алгоритм действует следующим образом. Он просматривает последовательно по строкам таблицы значений формул  . Если хотя бы один элемент нулевой строки
. Если хотя бы один элемент нулевой строки  равен 0, то без просмотра значения формулы
равен 0, то без просмотра значения формулы  в этой строке (т. е. числа
в этой строке (т. е. числа  ) происходит переход к просмотру следующей строки
) происходит переход к просмотру следующей строки  . Если все элементы
. Если все элементы  нулевой строки равны 1,
нулевой строки равны 1,
то просматривается значение 
 формулы
формулы  в этой строке. При
в этой строке. При  выдается результат:
выдается результат:
формула  не является логическим следствием формул
не является логическим следствием формул  . При
. При  происходит переход к просмотру следующей строки
происходит переход к просмотру следующей строки  . И так далее. Если после просмотра последней строки
. И так далее. Если после просмотра последней строки  должен произойти переход к просмотру следующей строки, то это означает, что определение логического следования выполнено и формула
должен произойти переход к просмотру следующей строки, то это означает, что определение логического следования выполнено и формула  является логическим следствием формул
является логическим следствием формул  .
.
Признаки логического следствия
То, что некоторая формула является логическим следствием какихто формул, можно выразить так же, сказав, что подходящая формула является тавтологией. В этом существо признаков, о которых пойдет речь в настоящем пункте, чем еще раз подчеркивается важное значение тавтологий.
Теорема 6.3 (признак логического следствия). Формула Нбудет логическим следствием формулы  тогда и только тогда, когда формула
тогда и только тогда, когда формула  является тавтологией:
является тавтологией:  .
.
Доказательство. Необходимость. Дано:  , т.е. если
, т.е. если

для набора высказываний  имеет место
имеет место  , то
, то
 . Тогда для любого набора высказываний
. Тогда для любого набора высказываний  имеет место равенство
имеет место равенство
поскольку равенство нулю возможно лишь в том случае, когда 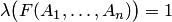 и
и
 , но такая ситуация исключена условием. Следовательно, на основании равенства (1.4)
, но такая ситуация исключена условием. Следовательно, на основании равенства (1.4)  для любых высказываний
для любых высказываний
 . Это означает, что формула
. Это означает, что формула  — тавтология,
— тавтология,
т.е.  .
.
Достаточность. Дано:  . Тогда:
. Тогда:
 для любых высказываний
для любых высказываний  , откуда в силу равенства (1.4)
, откуда в силу равенства (1.4)
Предположим теперь, что  . Тогда:
. Тогда: 
, откуда (на основании определения 1.7)  , ибо в противном случае
, ибо в противном случае
 — противоречие. Но это значит (по определению 6.1 логического следствия), что
— противоречие. Но это значит (по определению 6.1 логического следствия), что
 .
.
Следующая теорема дает признаки того, что формула является логическим следствием двух или большего количества формул.
Теорема 6.4. Для любых формул  следующие утверждения равносильны:
следующие утверждения равносильны:
а)  ;
;
б)  ;
;
в)  .
.
