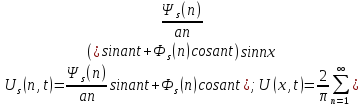|
31.
Т2.U(m)
гармон в D
и непрер вплоть до границы, достигает
своего наиб (наим) значения на границе
обл D.
U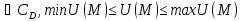 .
Д-во от
противного. Положим, что пусть сущ
внутр точка .
Д-во от
противного. Положим, что пусть сущ
внутр точка
 в кот и достигает своего максим
значения. Опишем сферическую поверхность
радиуса
из точки
в кот и достигает своего максим
значения. Опишем сферическую поверхность
радиуса
из точки
 .Границу
этой сферической поверхности обозначим
. .Границу
этой сферической поверхности обозначим
.
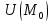 >U(M),
m=maxU(M) >U(M),
m=maxU(M)
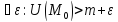 .
Обозн
точки, лежащие внутри или на сфере
через M(x,y,z)
, .
Обозн
точки, лежащие внутри или на сфере
через M(x,y,z)
,
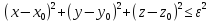 .
Можем
подобрать такое достаточно маленькое
,
что .
Можем
подобрать такое достаточно маленькое
,
что
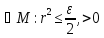 .
Введем всп ф-цию вида V(M)=U(M)+ .
Введем всп ф-цию вида V(M)=U(M)+ .Р-м
V(M)
внутри сферы
V( .Р-м
V(M)
внутри сферы
V(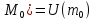 .
:V(M) .
:V(M) =>V( =>V(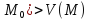 => что V
принимает наиб значение внутри сферы,
пусть это точка
=> что V
принимает наиб значение внутри сферы,
пусть это точка
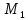 .
V( .
V(
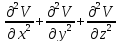 = =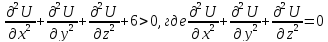 .
Получим
против, т.е. V
не может принимать макс знач во внутр
точке, => что U
не принимает макс значение во внутр
точке. Следствие. Если V
и U
гармон в D
и непрер вплоть до границы, то вып на
границе одного из нер-ств UV,
UV
влечет за собой вып этих нер-ств во
всей обл . Это следует из U-V0.
Пусть U
и V
являются непрер вместе со своими частн
произв вплоть до 2 порядка в D. .
Получим
против, т.е. V
не может принимать макс знач во внутр
точке, => что U
не принимает макс значение во внутр
точке. Следствие. Если V
и U
гармон в D
и непрер вплоть до границы, то вып на
границе одного из нер-ств UV,
UV
влечет за собой вып этих нер-ств во
всей обл . Это следует из U-V0.
Пусть U
и V
являются непрер вместе со своими частн
произв вплоть до 2 порядка в D.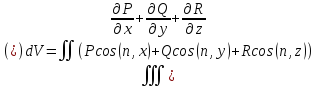 . .
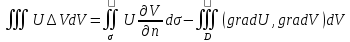 -1 ф-ла Грина. Поменяв местами U
и V,вычитая
из 1 получим:
-1 ф-ла Грина. Поменяв местами U
и V,вычитая
из 1 получим:
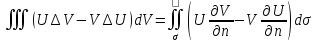 - 2ф-ла Грина.
- 2ф-ла Грина.
32.Пусть
U-
2ды непр дифф-ма в D
с границей S
(дост гладкой) и имеет непр 1ые производн,
непрер вплоть до границы, тогда для
произвольной внутр точки обл
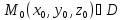 .
U( .
U(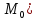 = =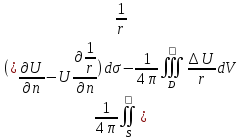 .
Док-во:
Бум сначала считать, что U
имеет 2 производные, непр вплоть до
границы. Введем в рассм ф-цию V=1/r,
применить к U
и V
ф-цию Грина непосредственно не можем,
т.к. V
в .
Док-во:
Бум сначала считать, что U
имеет 2 производные, непр вплоть до
границы. Введем в рассм ф-цию V=1/r,
применить к U
и V
ф-цию Грина непосредственно не можем,
т.к. V
в
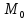 не определена. Ограничим сферой радиуса
точку
не определена. Ограничим сферой радиуса
точку
 .Применим
2 ф-лу Грина .Применим
2 ф-лу Грина
 .
Оценим 2 интеграл: .
Оценим 2 интеграл:
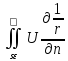 = =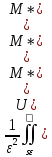 .
При .
При
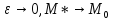 , ,
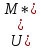 .
Т.к. U(M) .
Т.к. U(M)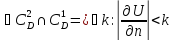 , ,
 - -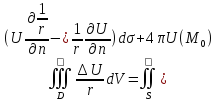 -3я ф-ла Грина.
-3я ф-ла Грина.
33.
Теор.
Р-м 3-ю
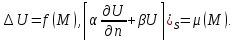 Решение
3краевой задачи для ур-ния Лапласа
единственно. Док-во:
положим Ǝ 2 решения U=U1+U2
гармонично
в D.
∆U=0 Решение
3краевой задачи для ур-ния Лапласа
единственно. Док-во:
положим Ǝ 2 решения U=U1+U2
гармонично
в D.
∆U=0
 .
Применим
к U
1ю формулу Грина, положив U=V.
0= .
Применим
к U
1ю формулу Грина, положив U=V.
0= .
Из граничного усл .
Из граничного усл
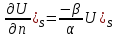 .
0= .
0= ,
т.к. U ,
т.к. U . .
34.Теор.
Р-ние внутр з-чи Неймана ур-ния Лапласа
(П) определяется с точн до const.
Д-во:
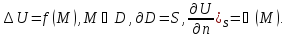 Р-м
внутр з-чу Неймана, бум считать что
2 реш-я U= Р-м
внутр з-чу Неймана, бум считать что
2 реш-я U=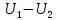 в силу
лин-сти з-чи и будет гармон в области
и удовл
в силу
лин-сти з-чи и будет гармон в области
и удовл
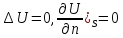 .
Восп 1й
формулой Грина положив V=U.
0= .
Восп 1й
формулой Грина положив V=U.
0=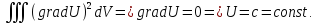 т.е. решение
внутр задачи Неймана не единственно.
т.е. решение
внутр задачи Неймана не единственно.
35.
Теор.
Р-ние внешн краевых задач для ур-ния
Лапласа (П) единств.
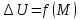 ,
U ,
U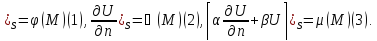 Док-во:Выберем
центр координат внутри замкн поверх-ти
S
и проведем сферу
Док-во:Выберем
центр координат внутри замкн поверх-ти
S
и проведем сферу
 ,
кот содержится внутри S. ,
кот содержится внутри S.
 -область
между S
и -область
между S
и
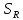 .
Полож, что в .
Полож, что в
 сущ 2 решения, кот содержатся внутри
S.
сущ 2 решения, кот содержатся внутри
S.
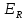 - обл между S
и
- обл между S
и
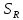 . .
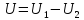 .Применим 1ю ф-лу Грина, полагая U=V
в области
.Применим 1ю ф-лу Грина, полагая U=V
в области
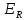 . .
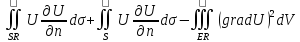 ,
где ,
где
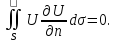 Для задачи
(1) (2) устремим R
к
: 0=- -
Для задачи
(1) (2) устремим R
к
: 0=- -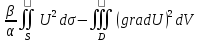 ,
|U|< ,
|U|<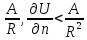 .
Т.е. пришли
к (*) :gradU=0
U=const
, U(M)=0
, ME
(для (3)). Для (1) (2) gradU=0
U(M)=const
, U0
, M
U0. .
Т.е. пришли
к (*) :gradU=0
U=const
, U(M)=0
, ME
(для (3)). Для (1) (2) gradU=0
U(M)=const
, U0
, M
U0.
36.Для
ф-ции
U(M)
задача Дирихле U(M)=0,
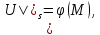 M M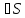 .
Введем .
Введем
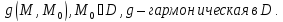
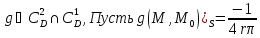 .
Применим
к g
и U
2ю ф-лу Грина: .
Применим
к g
и U
2ю ф-лу Грина:
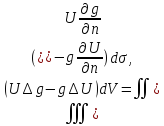
 0= 0=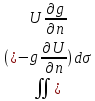 = =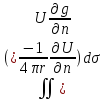 =0.
Вычтем =0.
Вычтем
 )d )d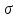 : :
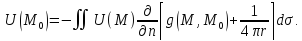 Обозн.
Обозн.
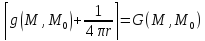 и вставим.
и вставим.
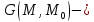 ф-ция
Грина внутр задачи Дирихле для ур-ния
Лапласа. Опр. Ф-цией Грина задачи
Дирихле для уравнения Лапласа называется
функция ф-ция
Грина внутр задачи Дирихле для ур-ния
Лапласа. Опр. Ф-цией Грина задачи
Дирихле для уравнения Лапласа называется
функция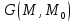 удовл условиям: 1.
удовл условиям: 1.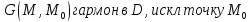 .
2.в D
ф-ция G
дополняет представление .
2.в D
ф-ция G
дополняет представление
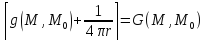 . 3.На
границе
. 3.На
границе

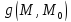 - регулярная часть ф-ции Грина. Свойства:
Ф-ция Грина
- регулярная часть ф-ции Грина. Свойства:
Ф-ция Грина
 .
2. .
2.
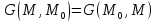 –симметрична.
–симметрична.
37.
Ф-я
Грина задачи Неймана для ур-ия Лапласа.
З-ча Неймана: ∆u(M)=0,M∈D
;
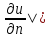 S
=ψ(M),M∈S
Если u
- гармон в D
, справедлива 3я ф-ла Грина: S
=ψ(M),M∈S
Если u
- гармон в D
, справедлива 3я ф-ла Грина:
 ; g(P,M)∈
; g(P,M)∈ -
гарм-ую ф-ю точки P,P∈D -
гарм-ую ф-ю точки P,P∈D
 ; ;
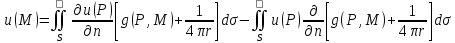 ;
G(P,M)=g(P,M)+ ;
G(P,M)=g(P,M)+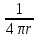 ; ;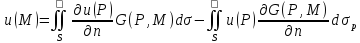 ;
Опр: Ф-ей Грина задачи Неймана для ур-я
Лапласа наз-ся G(P,M) обладающие св-ми:
1) Явл всюду гармон в обл D,
кроме P=M
, в кот обращается в бесконечность,
имеет непрерывную 1ю производную
вплоть до границы. 2) Допускает
представление G(P,M)=g(P,M)+ ;
Опр: Ф-ей Грина задачи Неймана для ур-я
Лапласа наз-ся G(P,M) обладающие св-ми:
1) Явл всюду гармон в обл D,
кроме P=M
, в кот обращается в бесконечность,
имеет непрерывную 1ю производную
вплоть до границы. 2) Допускает
представление G(P,M)=g(P,M)+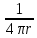 ,
g(P,M)-гармон
в D
и непрерывно дифферен-я вплоть до
границы.3) ; ,
g(P,M)-гармон
в D
и непрерывно дифферен-я вплоть до
границы.3) ;
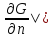 P∈S
= P∈S
=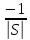 ,
|S|-
плотность поверх-ти ,
|S|-
плотность поверх-ти
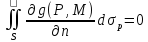 необх, чтобы
необх, чтобы
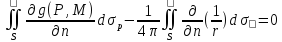 ;
получим 2ое слагаемое ;
получим 2ое слагаемое
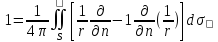 ; ;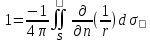 ; ;
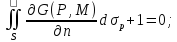
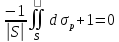 .
Используя ф-ю Грина, решение задачи
Неймана для ур-я Лапласа можно
представить: .
Используя ф-ю Грина, решение задачи
Неймана для ур-я Лапласа можно
представить:
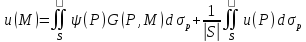
25.
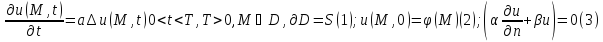 Т.
Реш задачи (1), (2), (3), непрер в заданной
области вместе со своими частн
производными 1го порядка, единств.
Док:
противное: сущ 2 реш задачи (1), (2), (3):
u1
и u2
. V
= u1-
u2
. V
– удовл однородной задаче.V|t
= 0 = 0
. Воспользуемся 1 ф-лой Грина, положив
u
= V. Т.
Реш задачи (1), (2), (3), непрер в заданной
области вместе со своими частн
производными 1го порядка, единств.
Док:
противное: сущ 2 реш задачи (1), (2), (3):
u1
и u2
. V
= u1-
u2
. V
– удовл однородной задаче.V|t
= 0 = 0
. Воспользуемся 1 ф-лой Грина, положив
u
= V. Проинтегрируем
это рав-тво по t
от 0 до Т.В левой части подынтегральная
ф-ция неотриц, значит интеграл в левой
части
0, интегралы в правой части ≤ 0, значит
выражения равны 0.=> V Проинтегрируем
это рав-тво по t
от 0 до Т.В левой части подынтегральная
ф-ция неотриц, значит интеграл в левой
части
0, интегралы в правой части ≤ 0, значит
выражения равны 0.=> V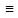 0 => u1
0 => u1
 u2
, значит
решение единственно.
u2
, значит
решение единственно.
26.Рассм
1ую краевую задачу для ур-ния 1ной
пространственной переменной.
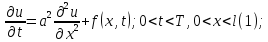 u(x,0)=
u(x,0)=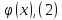 u(0,t)=μ1(t);
u(l,t)=μ2(t); u(0,t)=μ1(t);
u(l,t)=μ2(t);
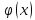 имеет кусочно непрер производную по
х.
имеет кусочно непрер производную по
х. .
Найдем все решения задачи .
Найдем все решения задачи
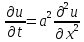 ;
u(0,t)=0;
u(l,t)=0;u(x,t)=X(x)T(t); ;
u(0,t)=0;
u(l,t)=0;u(x,t)=X(x)T(t);
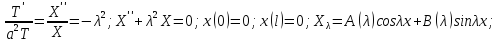 подставляем в граничные условия и
получаем,что A=0,
а
подставляем в граничные условия и
получаем,что A=0,
а
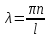 ; ;
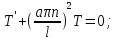
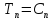 exp(- exp(-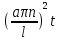 );
тогда общее реш: );
тогда общее реш:
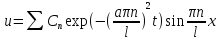 ;
найдем ;
найдем
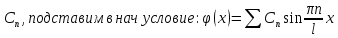 ; ;
 .Рассм
(1), (2),
(3)u(x,0)
= 0, f
C,
t
> 0 (2)f(0,t)
= f(l,
t)
= 0.f
– непрер и имеет кусочно-непрерывную
производную по t.
Будем искать решение задачи в виде: .Рассм
(1), (2),
(3)u(x,0)
= 0, f
C,
t
> 0 (2)f(0,t)
= f(l,
t)
= 0.f
– непрер и имеет кусочно-непрерывную
производную по t.
Будем искать решение задачи в виде:
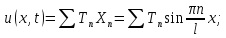 подставляем
в ур-ние: подставляем
в ур-ние: ; ;
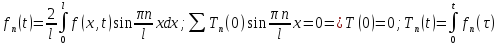 exp(-
exp(-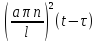 )dτ.
Тогда реш задачи: )dτ.
Тогда реш задачи:
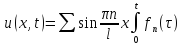 exp(-
exp(-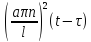 )dτ. )dτ.
27.
Остановимся
на изучении процесса распространения
тепла в неогран стержне.
 Из всех возможных условий на
бесконечности, будем рассм условие
ограниченности на бесконечности.
Из всех возможных условий на
бесконечности, будем рассм условие
ограниченности на бесконечности.
 .
Восп методом фурье разделения перем .
Восп методом фурье разделения перем

 exp(- exp(-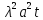 ); );
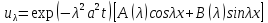 .
Так как
- произвольная, то если воспользоваться
всеми возможными ,
то .
Так как
- произвольная, то если воспользоваться
всеми возможными ,
то
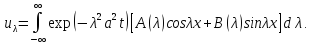 Это будет решением, если интеграл
равномерно сх-ся. Если функция
периодическая, то этот ряд определяет
ф-цию на всей числовой прямой.
Это будет решением, если интеграл
равномерно сх-ся. Если функция
периодическая, то этот ряд определяет
ф-цию на всей числовой прямой.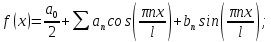
 .
f .
f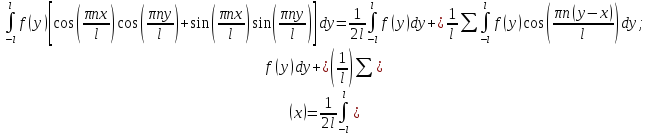
 ; ;
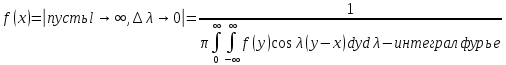 Подставим
наше реш в начал усл: Подставим
наше реш в начал усл: .
Интеграл фурье для .
Интеграл фурье для
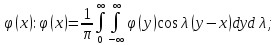
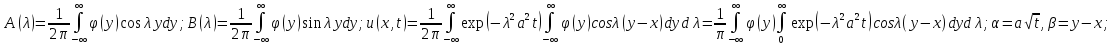 Подставим замену и получим:
Подставим замену и получим: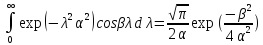 ; ;
 То
есть мы получили явный вид реш задачи
Коши. наз формулой Пуассона, интеграл
справа наз интегралом Пуассона. То
есть мы получили явный вид реш задачи
Коши. наз формулой Пуассона, интеграл
справа наз интегралом Пуассона.

28.Опр.
Ф-цией Грина задачи Коши (1), (2) наз ф-ция
G(M,t,p),
где M(x,y,z)
явл реш задачи Коши.
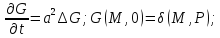
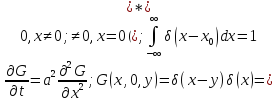 Построим
ф-цию Грина , восп формулой Пуассона: Построим
ф-цию Грина , восп формулой Пуассона: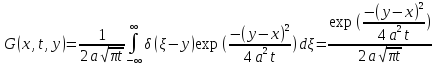 То
есть фундамент реш задачи Коши явл
ф-цией Грина.Будем считать, что в нек
момент времени участку [x0-h,x0+h]
сообщили количество тепла Q=2hcpUo,
где Uo-
показывает на сколько повысилась
температура. В этом случае ф-ла Пуассона: То
есть фундамент реш задачи Коши явл
ф-цией Грина.Будем считать, что в нек
момент времени участку [x0-h,x0+h]
сообщили количество тепла Q=2hcpUo,
где Uo-
показывает на сколько повысилась
температура. В этом случае ф-ла Пуассона:
 .Уменьшаем
начал участок и стягиваем его к точке,
то есть h
0. Но ранее восп теоремой о среднем: .Уменьшаем
начал участок и стягиваем его к точке,
то есть h
0. Но ранее восп теоремой о среднем:
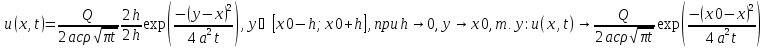 То
есть ф-ция Грина определяет распределение
температур в стержне в резул воздействия
мгновенного точечного источника. То
есть ф-ция Грина определяет распределение
температур в стержне в резул воздействия
мгновенного точечного источника.
29.
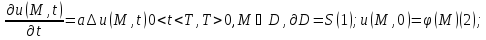 Л1.
Если
яв-тся нечетной относительно нуля, то
u(0,t)
Док. Решение задачи по формуле Пуассона Л1.
Если
яв-тся нечетной относительно нуля, то
u(0,t)
Док. Решение задачи по формуле Пуассона
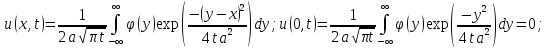 Лемма
2. Если в (1), (2) )
является четной относительно нуля,
то Лемма
2. Если в (1), (2) )
является четной относительно нуля,
то
 Док. Док.
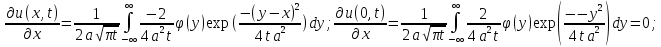 Р-м
след задачу: Р-м
след задачу: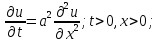 u(x,0)=
u(x,0)=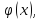 u(0,t)=0
(6); u(0,t)=0
(6);
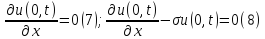 .Рассм
(1), (2), (6). Продолжим
нечетным образом. U(x,
t)
удовлетворяет задаче с .Рассм
(1), (2), (6). Продолжим
нечетным образом. U(x,
t)
удовлетворяет задаче с
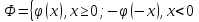 . .
 Для
(1), (2), (7) : Для
(1), (2), (7) :
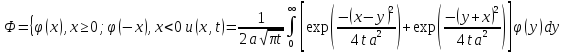
30.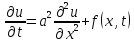 ;
U(M,t)=U(m); ;
U(M,t)=U(m);
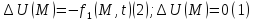 Опр.
Ф-ция
U(M)
наз гармонической в D
(конечная область с кусочно- гладкой
границей D Опр.
Ф-ция
U(M)
наз гармонической в D
(конечная область с кусочно- гладкой
границей D ),
если она непрерыв со своими частн
произв до 2-го порядка и удовл ур-нию
Лапласа.Опр. Ф-ция U(M)
наз гармонической в неограниченной
области Е, если она непрерывна в Е
вместе со своими частными производными
до 2-го порядка , удовл ур-нию Лапласа
и убывает при стремлении ),
если она непрерыв со своими частн
произв до 2-го порядка и удовл ур-нию
Лапласа.Опр. Ф-ция U(M)
наз гармонической в неограниченной
области Е, если она непрерывна в Е
вместе со своими частными производными
до 2-го порядка , удовл ур-нию Лапласа
и убывает при стремлении
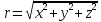 к
бесконечности, т.е. к
бесконечности, т.е.
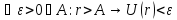 .
1.Пусть
D-
ограниченная область с кусочно-гладкой
границей, а Е- неограниченная область. .
1.Пусть
D-
ограниченная область с кусочно-гладкой
границей, а Е- неограниченная область.
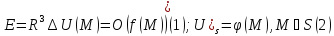 .
(1)(2)- задача Дирихле может быть внутр,
если решается в D,
внешней, если в E. .
(1)(2)- задача Дирихле может быть внутр,
если решается в D,
внешней, если в E.
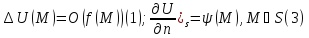 .(1)(3)
– задача Неймана, n-
внешняя нормаль к S. .(1)(3)
– задача Неймана, n-
внешняя нормаль к S.
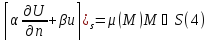 (1)(4) – 3я краевая задача.Пусть U
и V
явл непрерывными вместе со своими
частными производными вплоть до
второго порядка в D.
(1)(4) – 3я краевая задача.Пусть U
и V
явл непрерывными вместе со своими
частными производными вплоть до
второго порядка в D.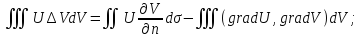 (5)– первая формула Грина.Аналогично
поменяв местами U
и V,
и вычитая это из (5) получим
(5)– первая формула Грина.Аналогично
поменяв местами U
и V,
и вычитая это из (5) получим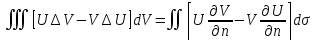 (6)-вторая формула Грина.
(6)-вторая формула Грина.
39.
Сл из Ф-лы Пуассона.
Рассмотрим ф-ю u(M)-
гармоническую в D
и всюду положительную: u(M)>0,M∈D
.Возьмем произвольную точку M0∈D
. Проведем из нее шар радиуса R
, целиком лежащий в D
и выберем другую произвольную точку
M,
лежащую в шаре. R
+ ρ
≥ r
≥ R-ρ;
R
+ ρ
≥ r
≥ R-ρ;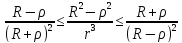 Умножим нер-во на u(P)
и проинтегрируем все части нер-ва на
сфере:
Умножим нер-во на u(P)
и проинтегрируем все части нер-ва на
сфере:
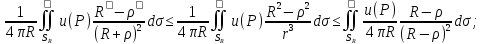 По Т о среднем:
По Т о среднем:
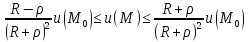 – нер-во Гарнака.
– нер-во Гарнака.
38.
внутренняя задача
Дирихле для шара радиуса R:
∆u(M)
= 0,
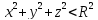 ;
U|x^2+y^2+z^2=R^2
= φ(M).
Построим ф-ю Грина для шара радиуса
R.
Выберем внутри шара произвольную
точку M(x,y,z)
. Проведем инверсию точки относительно
сферы и получим точку. |OM|=ρ,
|OM1|=ρ1
,ρρ1=R2
; ;
U|x^2+y^2+z^2=R^2
= φ(M).
Построим ф-ю Грина для шара радиуса
R.
Выберем внутри шара произвольную
точку M(x,y,z)
. Проведем инверсию точки относительно
сферы и получим точку. |OM|=ρ,
|OM1|=ρ1
,ρρ1=R2
;
 ; ;
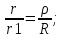
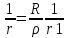 ;
ф-ю Грина можно представить ;
ф-ю Грина можно представить
 ; ;
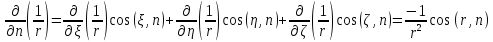 ; ;
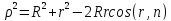 ;
cos(r,n)= ;
cos(r,n)=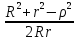 ; ; ;
(9) u(M)= ;
(9) u(M)=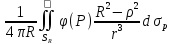 -
ф-ла Пуассона. Покажем, что правая
часть (9) удовлетворяет условию Лапласа.
При φ≡1 (9): 1= -
ф-ла Пуассона. Покажем, что правая
часть (9) удовлетворяет условию Лапласа.
При φ≡1 (9): 1=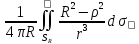 ;u(M)
- φ(N)=|M⟶N|= ;u(M)
- φ(N)=|M⟶N|=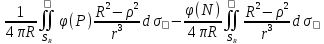 Проведем из выбранной точки N
шар радиуса 2δ
.
Проведем из выбранной точки N
шар радиуса 2δ
. -
часть поверхности SR,
попавшая в шар -
часть поверхности SR,
попавшая в шар
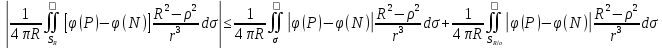 ;
|PN|<2δ
⇒|
φ(P)-φ(N)|<ε/2; ;
|PN|<2δ
⇒|
φ(P)-φ(N)|<ε/2;
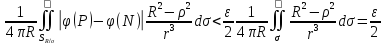 ,
|MN|≤δ; ,
|MN|≤δ;
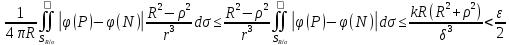 ; M⟶N⇒R2
- ρ2⟶0;
|u(M)-φ(N)|<ε.
Замеч: Решение внутренней задачи
Дирихле для круга описывается в виде
интеграла Пуассона:
; M⟶N⇒R2
- ρ2⟶0;
|u(M)-φ(N)|<ε.
Замеч: Решение внутренней задачи
Дирихле для круга описывается в виде
интеграла Пуассона: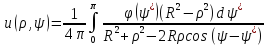 .
Внешняя задача Дирихле для шара:
∆u(M)=0
, .
Внешняя задача Дирихле для шара:
∆u(M)=0
,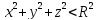 ;
U|x^2+y^2+z^2=R^2
= φ(M).
Решение задачи можно представить в
виде: ;
U|x^2+y^2+z^2=R^2
= φ(M).
Решение задачи можно представить в
виде:
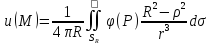 . .
41.(Т_Лиувилля)Ф-я,
гармон
в ∀
конечной области и огранич сверху или
снизу, явл постоянной.Д-во: Пусть ф-я
u(M)
- гармон в ∀
конечной обл.Если огра снизу:u(M)≥c,c=const,
сверху:-u(M)<-c
Рассмотрим огран снизу:u(M)>0-
гармоническая в ∀
конечной области.Зафиксируем произв
точку M
и проведем из начала координат сферу
радиуса R
так, чтобы M
лежала внутри шара.u-
гармон в шаре.Тогда, для нее справедливо
нерав-во Гарнака: (R-ρ)Ru(0)/(R+ρ)2≤u(M)≤
(R+ρ)Ru(0)/(R-ρ)2
Устремим
R⟶∞
:u(0)≤u(M)≤u(0)
В силу произвольности выбора M:
u(M)=u(0)=const.
40.
Т: Ф-я, гармон
во всем пр-ве, тождественно равна 0.
Д-во:Пусть u(M)
- функция гармон во всем пр-ве.Проведем
сферу из начала коорд радиуса R
, u-
будет гармон вне шара.Тогда ее можно
представить через значение на
поверхности формулу Пуассона для
внешней задачи Дирихле в точке на
поверхности: u(M)
= (1/4πR)
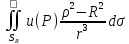 Из ∆ ОМР: R>ρ-r.Выберем
радиус сферы настолько большой если
ρ>2R,то
r>ρ/2
Из ∆ ОМР: R>ρ-r.Выберем
радиус сферы настолько большой если
ρ>2R,то
r>ρ/2
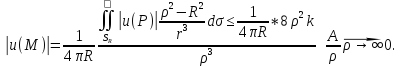
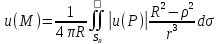
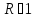 ,
|u(P)|<ε, ,
|u(P)|<ε,
 ,
|u(M)|<ε⇒u(M)≡0 ,
|u(M)|<ε⇒u(M)≡0
42.
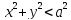 ;
U|x^2+y^2=a^2
= ;
U|x^2+y^2=a^2
= ;в
полярных: x=ρcosφ,
0≤ ρ ≤a,
y=
ρsinφ,
0≤ φ ≤2π;
u(x,y)
= u(ρ,φ); ;в
полярных: x=ρcosφ,
0≤ ρ ≤a,
y=
ρsinφ,
0≤ φ ≤2π;
u(x,y)
= u(ρ,φ);
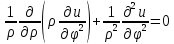 ;(1) ;(1)
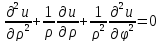 ;
(2) u(a,φ)=f(φ);
(3) u(ρ,φ+2πn)
= u(ρ,φ);
Найдем все нетривиальные реш (1),удовл
условию (3).U(ρ,φ)=R(ρ)Φ(φ); ;
(2) u(a,φ)=f(φ);
(3) u(ρ,φ+2πn)
= u(ρ,φ);
Найдем все нетривиальные реш (1),удовл
условию (3).U(ρ,φ)=R(ρ)Φ(φ);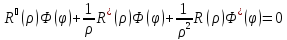 .Разделим
на u≢0
и .Разделим
на u≢0
и
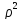 : :
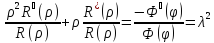 ; ;
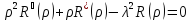 ; ;
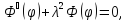
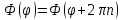 ;1)λ=0, ;1)λ=0,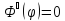 , ,
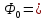 c1φ+c2
⇒
c1=0, c1φ+c2
⇒
c1=0,
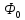 =c0=const;
2) λ≢0: =c0=const;
2) λ≢0:
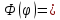 c1cosλφ
+ c2sinλφ,
λ=k=±1,±2; c1cosλφ
+ c2sinλφ,
λ=k=±1,±2;
 ;
Введем замену: t=
lnρ
R(ρ)=y(t), ;
Введем замену: t=
lnρ
R(ρ)=y(t),
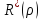 =
=
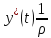 , ,
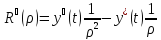 .
Подставим производные в уравнение: .
Подставим производные в уравнение:
 ;
k=0: ;
k=0:
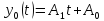 k
k 0: 0:
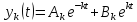 ; ;
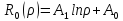 , ,
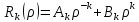 ; ;
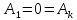 ;
; ;
;
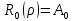 ; ;
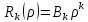 ; ;
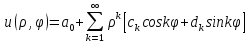 .
При ρ=A: .
При ρ=A:
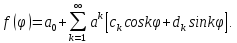
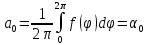 ; ;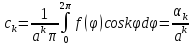 ; ;
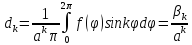 .
Решение внутренней задачи Дирихле
для круга принимает вид: .
Решение внутренней задачи Дирихле
для круга принимает вид: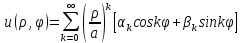 . .
43
 Рассм.
когда М вне D.(N)
интегрируема в D. Рассм.
когда М вне D.(N)
интегрируема в D. .При
удалении М от обл D .При
удалении М от обл D
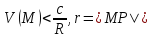 Р -произвольная точка, R
– расст от нач коорд.Поместим нач
коорд в точку О,
Р -произвольная точка, R
– расст от нач коорд.Поместим нач
коорд в точку О,
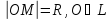 ,
d-диаметр
D. ,
d-диаметр
D.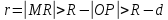 Бум считать, что М на столько удалена
от D,
что
Бум считать, что М на столько удалена
от D,
что
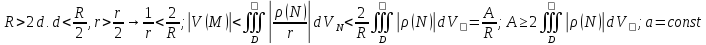 Обратим внимание, что
Обратим внимание, что
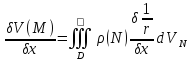 .Когда
МD,
V-
имеет непрерыв частн произв 1 порядка,
2 и т.д. .Когда
МD,
V-
имеет непрерыв частн произв 1 порядка,
2 и т.д.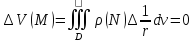 т.е. V-
непрер, имеет непрер частн произв,
удовлт уравнению Лапласа и стремится
на
т.е. V-
непрер, имеет непрер частн произв,
удовлт уравнению Лапласа и стремится
на
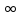 к 0, т.е. V
– гармонично вне D,
когда МD.Пусть
МD
если (N)<C
, то V-
непрерывна внутри D,
т.е. интеграл сходится равномерно во
внутр точках. Выделим
окрестность ()
то,
к 0, т.е. V
– гармонично вне D,
когда МD.Пусть
МD
если (N)<C
, то V-
непрерывна внутри D,
т.е. интеграл сходится равномерно во
внутр точках. Выделим
окрестность ()
то,
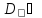 -
окрестности -
окрестности

 ,т.о.
интеграл сходится равномерно в любой
внутр точке M0,
а отсюда являющейся U(M)
непрер, при МD.Теорема.
Если ,т.о.
интеграл сходится равномерно в любой
внутр точке M0,
а отсюда являющейся U(M)
непрер, при МD.Теорема.
Если
 - плотн объемного потенциала – огранич
в D,
то потенциал объема (1) является
функцией, непрерыв вместе с частными
производными 1 порядка во всем
пространстве. Эти производные могут
быть получены дифференц-ем под знаком
интеграла. Теор. Если плотность
объемного потенциала (N)
непрер в обл D
и непрер 1ые производные, то объемный
потенциал (1) в D
имеет непрер частные производные 2го
порядка и удовл внутри D
уравнению Пуассона. Замечание. Если
имеется уравнение Пуассона
- плотн объемного потенциала – огранич
в D,
то потенциал объема (1) является
функцией, непрерыв вместе с частными
производными 1 порядка во всем
пространстве. Эти производные могут
быть получены дифференц-ем под знаком
интеграла. Теор. Если плотность
объемного потенциала (N)
непрер в обл D
и непрер 1ые производные, то объемный
потенциал (1) в D
имеет непрер частные производные 2го
порядка и удовл внутри D
уравнению Пуассона. Замечание. Если
имеется уравнение Пуассона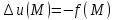 ,
то внутри D
это уравнение имеет частное решение ,
то внутри D
это уравнение имеет частное решение
 . .
44
Замкнут поверхность
S
наз поверхность Ляпунова, если выполнены
следующие условия : 1. для каждой точки
M
S
сущ определенная касательная
плоскость.2.
d
> 0 : N
S
сфера радиуса d
или меньшего, проведенная из N,
делит поверхность на 2 части, одна
лежит внутри сферы, другая – вне, при
этом прямые параллельные нормали в
точке N
пересекают часть поверхности в одной
точке. 3. Пусть
– острый угол между нормалями,
проведенными в двух произвольных
точках поверхности S,
r
– расстояние между этими точками, то
2 числа a
> 0, 0 <
<1, такие, что для любых точек.
 .Таким
образом второе условие обеспеч нам ,
чтобы z
= f(x,
y).
Третье условие обеспеч непрерывн
производных.В дальнейшем будем считать
все поверхности поверхностями
Ляпунова.Будем рассматривать потенциал
двойного слоя : .Таким
образом второе условие обеспеч нам ,
чтобы z
= f(x,
y).
Третье условие обеспеч непрерывн
производных.В дальнейшем будем считать
все поверхности поверхностями
Ляпунова.Будем рассматривать потенциал
двойного слоя : , ,
 -прямое
значение, M= -прямое
значение, M= .MN0
изнутри или извне, и .MN0
изнутри или извне, и
 предельное
внутр значение и если
равный конечный предел предельное
внутр значение и если
равный конечный предел
 внешнее выделенное значение.Если
плотность потенциала двойного слоя
внешнее выделенное значение.Если
плотность потенциала двойного слоя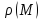 - непрерывна, то предельные значения
потенциала
и имеют место формулы.
- непрерывна, то предельные значения
потенциала
и имеют место формулы.
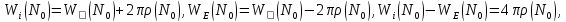 Замечание.
Потенциал двойного слоя равномерно
стремится к своим предельным значениям
изнутри и извне Теорема. Рассмотрим
потенциал простого слоя:Потенциал
простого слоя с непрерывной плотностью-
функция, непрерывная во всем пространстве. Замечание.
Потенциал двойного слоя равномерно
стремится к своим предельным значениям
изнутри и извне Теорема. Рассмотрим
потенциал простого слоя:Потенциал
простого слоя с непрерывной плотностью-
функция, непрерывная во всем пространстве.
45
Рассм обл D
3-х мерного пр-ва, опред пов-тью Ляпунова.
(1)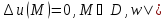 s=f(M),
M s=f(M),
M -
внутр.задача Дирихле. (2) ) -
внутр.задача Дирихле. (2) )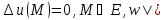 s=f(M),
M s=f(M),
M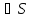 -внешняя
задача Дирихле (3) ) -внешняя
задача Дирихле (3) )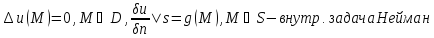 а,
(4) а,
(4)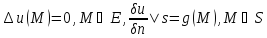 -внешн.задача
Неймана.Ищем решение задачи Дирихле
в виде потенциала двойного слоя с
неизв плотностью. -внешн.задача
Неймана.Ищем решение задачи Дирихле
в виде потенциала двойного слоя с
неизв плотностью.
 для(1-2).Рассм.(1). Для того чтобы w
была реш задачи (1) необходимо: N0S.
для(1-2).Рассм.(1). Для того чтобы w
была реш задачи (1) необходимо: N0S.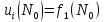 .
По теореме о разрывности потенциала
второго слоя можно .
По теореме о разрывности потенциала
второго слоя можно
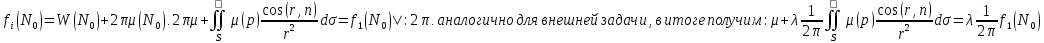 , ,
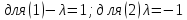 .
Для задач Неймана будем
искать
реш в виде потенциала простого слоя. .
Для задач Неймана будем
искать
реш в виде потенциала простого слоя.
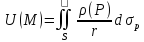 , ,
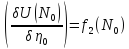 .
Получим .
Получим
 ,для ,для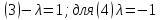 . .
46
Пусть дана нек функцияf(x),
если задан нек интервал [a,b]
и известна функция двух переменных
К(x,),
то
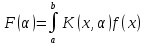 (1) называется интегральнымым
преобразованиемК(x,)
– ядро интеграла преобразования, а
[a,b]
интервалом интегрируемого преобразования.
(1) называется интегральнымым
преобразованиемК(x,)
– ядро интеграла преобразования, а
[a,b]
интервалом интегрируемого преобразования. (2), если имеется интеграл преобразования.Если
(2), если имеется интеграл преобразования.Если
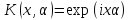 на
на
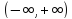 ,
то соответств интеграл преобразования
называется преобразованием Фурье.Если ,
то соответств интеграл преобразования
называется преобразованием Фурье.Если
 (3) это обозначение преобразования
Фурье.Если исходная функция f(r)
является интегрируемой на (-,
+)
(f(r)
L(-,
+))
и интеграл
(3) это обозначение преобразования
Фурье.Если исходная функция f(r)
является интегрируемой на (-,
+)
(f(r)
L(-,
+))
и интеграл
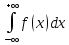 сходится
абсолютно (при этом сходится
абсолютно (при этом
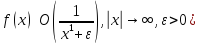 При
этом обращение преобразования Фурье
задается формулой. При
этом обращение преобразования Фурье
задается формулой.
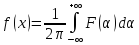 Св-ва преобраз Фурье.1.
Св-ва преобраз Фурье.1.
 2.
2.
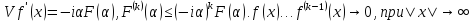 3.
3.
 .
4. .
4.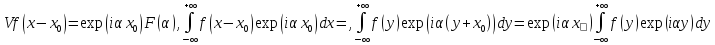 5.
5.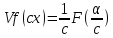 , ,
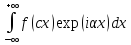 = =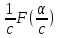
47_1
 , ,
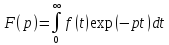 (1) преобраз Лапласа.
(1) преобраз Лапласа.
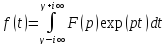 Где
Где
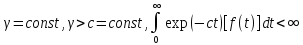 сх-ся. Отметим условия кот накладываются
на f(t)
как следствие из свойств F(p)1.
если F(p)
– анал ф-ция комплексной перем
сх-ся. Отметим условия кот накладываются
на f(t)
как следствие из свойств F(p)1.
если F(p)
– анал ф-ция комплексной перем
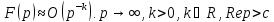 ,
то ,
то
 и
является преобразованием Лапласа,
для f(t)
такой, что f(t)
непрерывна
и
является преобразованием Лапласа,
для f(t)
такой, что f(t)
непрерывна
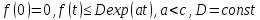 Если
функция имеет преобразования Лапласа,
то оно единственно.Если две функции
имеют одинаковые преобразования
Лапласа, то они различны на множестве
точек меры О. Пусть имеются две функции
f(t)
и g(t)
, t0,
и соответственно F(p)
и G(p)
– их преобразования Лапласа, то
справедливо соотношение: Если
функция имеет преобразования Лапласа,
то оно единственно.Если две функции
имеют одинаковые преобразования
Лапласа, то они различны на множестве
точек меры О. Пусть имеются две функции
f(t)
и g(t)
, t0,
и соответственно F(p)
и G(p)
– их преобразования Лапласа, то
справедливо соотношение:

47_2
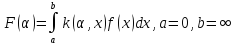 При
При
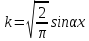 это преобразование называется
синус-преобразование Фурье.
это преобразование называется
синус-преобразование Фурье. (2)
– косинус-преобразование Фурьеf(x)
должна быть абсолютно интегрируемой
на [0, +)
Свойства преобразований Фурье на
полупрямой. (2)
– косинус-преобразование Фурьеf(x)
должна быть абсолютно интегрируемой
на [0, +)
Свойства преобразований Фурье на
полупрямой.
1.
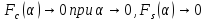 ; ;
 2. 2.
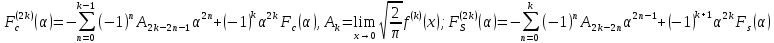
3.заебалась
формул куча!4. Свойство сверток.
 -
соответствующие преобразования Фурье
функций f(x)
и g(x). -
соответствующие преобразования Фурье
функций f(x)
и g(x).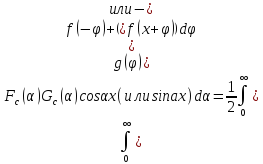
48Рассм
f(x)
,x0,.
В этом случае
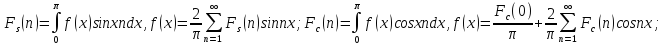 Пример.
Применим конечное преобразование
Фурье к задаче о колебании струны с
закрепл концами. Пример.
Применим конечное преобразование
Фурье к задаче о колебании струны с
закрепл концами.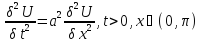 , ,
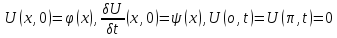 Обозн
Обозн
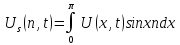 , ,
 , ,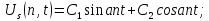 в
итоге: в
итоге:
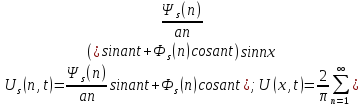
|


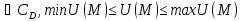 .
Д-во от
противного. Положим, что пусть сущ
внутр точка
.
Д-во от
противного. Положим, что пусть сущ
внутр точка
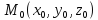 в кот и достигает своего максим
значения. Опишем сферическую поверхность
радиуса
из точки
в кот и достигает своего максим
значения. Опишем сферическую поверхность
радиуса
из точки
 .Границу
этой сферической поверхности обозначим
.
.Границу
этой сферической поверхности обозначим
.
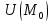 >U(M),
m=maxU(M)
>U(M),
m=maxU(M)
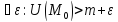 .
Обозн
точки, лежащие внутри или на сфере
через M(x,y,z)
,
.
Обозн
точки, лежащие внутри или на сфере
через M(x,y,z)
,
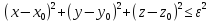 .
Можем
подобрать такое достаточно маленькое
,
что
.
Можем
подобрать такое достаточно маленькое
,
что
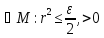 .
Введем всп ф-цию вида V(M)=U(M)+
.
Введем всп ф-цию вида V(M)=U(M)+ .Р-м
V(M)
внутри сферы
V(
.Р-м
V(M)
внутри сферы
V(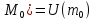 .
:V(M)
.
:V(M) =>V(
=>V(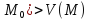 => что V
принимает наиб значение внутри сферы,
пусть это точка
=> что V
принимает наиб значение внутри сферы,
пусть это точка
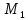 .
V(
.
V(
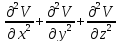 =
=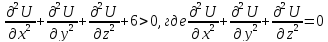 .
Получим
против, т.е. V
не может принимать макс знач во внутр
точке, => что U
не принимает макс значение во внутр
точке. Следствие. Если V
и U
гармон в D
и непрер вплоть до границы, то вып на
границе одного из нер-ств UV,
UV
влечет за собой вып этих нер-ств во
всей обл . Это следует из U-V0.
Пусть U
и V
являются непрер вместе со своими частн
произв вплоть до 2 порядка в D.
.
Получим
против, т.е. V
не может принимать макс знач во внутр
точке, => что U
не принимает макс значение во внутр
точке. Следствие. Если V
и U
гармон в D
и непрер вплоть до границы, то вып на
границе одного из нер-ств UV,
UV
влечет за собой вып этих нер-ств во
всей обл . Это следует из U-V0.
Пусть U
и V
являются непрер вместе со своими частн
произв вплоть до 2 порядка в D.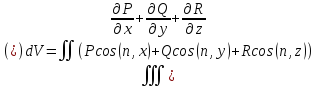 .
.
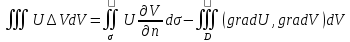 -1 ф-ла Грина. Поменяв местами U
и V,вычитая
из 1 получим:
-1 ф-ла Грина. Поменяв местами U
и V,вычитая
из 1 получим:
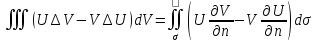 - 2ф-ла Грина.
- 2ф-ла Грина.
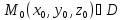 .
U(
.
U(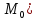 =
=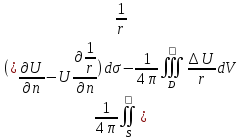 .
Док-во:
Бум сначала считать, что U
имеет 2 производные, непр вплоть до
границы. Введем в рассм ф-цию V=1/r,
применить к U
и V
ф-цию Грина непосредственно не можем,
т.к. V
в
.
Док-во:
Бум сначала считать, что U
имеет 2 производные, непр вплоть до
границы. Введем в рассм ф-цию V=1/r,
применить к U
и V
ф-цию Грина непосредственно не можем,
т.к. V
в
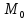 не определена. Ограничим сферой радиуса
точку
не определена. Ограничим сферой радиуса
точку
 .Применим
2 ф-лу Грина
.Применим
2 ф-лу Грина
 .
Оценим 2 интеграл:
.
Оценим 2 интеграл:
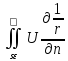 =
=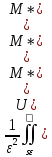 .
При
.
При
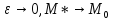 ,
,
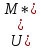 .
Т.к. U(M)
.
Т.к. U(M)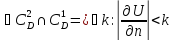 ,
,
 -
-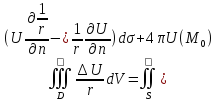 -3я ф-ла Грина.
-3я ф-ла Грина.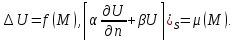 Решение
3краевой задачи для ур-ния Лапласа
единственно. Док-во:
положим Ǝ 2 решения U=U1+U2
гармонично
в D.
∆U=0
Решение
3краевой задачи для ур-ния Лапласа
единственно. Док-во:
положим Ǝ 2 решения U=U1+U2
гармонично
в D.
∆U=0
 .
Применим
к U
1ю формулу Грина, положив U=V.
0=
.
Применим
к U
1ю формулу Грина, положив U=V.
0= .
Из граничного усл
.
Из граничного усл
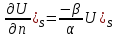 .
0=
.
0= ,
т.к. U
,
т.к. U .
.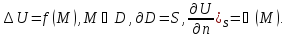 Р-м
внутр з-чу Неймана, бум считать что
2 реш-я U=
Р-м
внутр з-чу Неймана, бум считать что
2 реш-я U=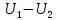 в силу
лин-сти з-чи и будет гармон в области
и удовл
в силу
лин-сти з-чи и будет гармон в области
и удовл
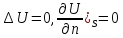 .
Восп 1й
формулой Грина положив V=U.
0=
.
Восп 1й
формулой Грина положив V=U.
0=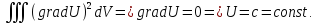 т.е. решение
внутр задачи Неймана не единственно.
т.е. решение
внутр задачи Неймана не единственно.
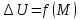 ,
U
,
U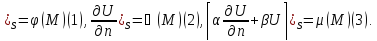 Док-во:Выберем
центр координат внутри замкн поверх-ти
S
и проведем сферу
Док-во:Выберем
центр координат внутри замкн поверх-ти
S
и проведем сферу
 ,
кот содержится внутри S.
,
кот содержится внутри S.
 -область
между S
и
-область
между S
и
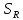 .
Полож, что в
.
Полож, что в
 сущ 2 решения, кот содержатся внутри
S.
сущ 2 решения, кот содержатся внутри
S.
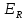 - обл между S
и
- обл между S
и
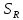 .
.
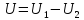 .Применим 1ю ф-лу Грина, полагая U=V
в области
.Применим 1ю ф-лу Грина, полагая U=V
в области
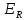 .
.
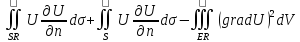 ,
где
,
где
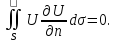 Для задачи
(1) (2) устремим R
к
: 0=- -
Для задачи
(1) (2) устремим R
к
: 0=- -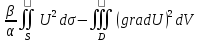 ,
|U|<
,
|U|<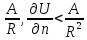 .
Т.е. пришли
к (*) :gradU=0
U=const
, U(M)=0
, ME
(для (3)). Для (1) (2) gradU=0
U(M)=const
, U0
, M
U0.
.
Т.е. пришли
к (*) :gradU=0
U=const
, U(M)=0
, ME
(для (3)). Для (1) (2) gradU=0
U(M)=const
, U0
, M
U0.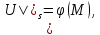 M
M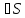 .
Введем
.
Введем
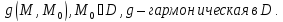
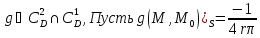 .
Применим
к g
и U
2ю ф-лу Грина:
.
Применим
к g
и U
2ю ф-лу Грина:
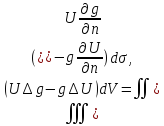
 0=
0=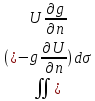 =
=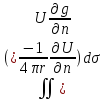 =0.
Вычтем
=0.
Вычтем
 )d
)d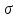 :
:
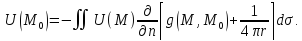 Обозн.
Обозн.
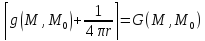 и вставим.
и вставим.
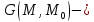 ф-ция
Грина внутр задачи Дирихле для ур-ния
Лапласа. Опр. Ф-цией Грина задачи
Дирихле для уравнения Лапласа называется
функция
ф-ция
Грина внутр задачи Дирихле для ур-ния
Лапласа. Опр. Ф-цией Грина задачи
Дирихле для уравнения Лапласа называется
функция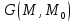 удовл условиям: 1.
удовл условиям: 1.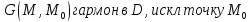 .
2.в D
ф-ция G
дополняет представление
.
2.в D
ф-ция G
дополняет представление
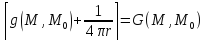 . 3.На
границе
. 3.На
границе

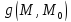 - регулярная часть ф-ции Грина. Свойства:
Ф-ция Грина
- регулярная часть ф-ции Грина. Свойства:
Ф-ция Грина
 .
2.
.
2.
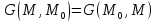 –симметрична.
–симметрична.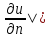 S
=ψ(M),M∈S
Если u
- гармон в D
, справедлива 3я ф-ла Грина:
S
=ψ(M),M∈S
Если u
- гармон в D
, справедлива 3я ф-ла Грина:
 ; g(P,M)∈
; g(P,M)∈ -
гарм-ую ф-ю точки P,P∈D
-
гарм-ую ф-ю точки P,P∈D
 ;
;
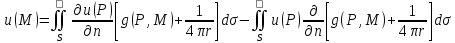 ;
G(P,M)=g(P,M)+
;
G(P,M)=g(P,M)+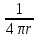 ;
;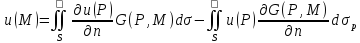 ;
Опр: Ф-ей Грина задачи Неймана для ур-я
Лапласа наз-ся G(P,M) обладающие св-ми:
1) Явл всюду гармон в обл D,
кроме P=M
, в кот обращается в бесконечность,
имеет непрерывную 1ю производную
вплоть до границы. 2) Допускает
представление G(P,M)=g(P,M)+
;
Опр: Ф-ей Грина задачи Неймана для ур-я
Лапласа наз-ся G(P,M) обладающие св-ми:
1) Явл всюду гармон в обл D,
кроме P=M
, в кот обращается в бесконечность,
имеет непрерывную 1ю производную
вплоть до границы. 2) Допускает
представление G(P,M)=g(P,M)+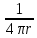 ,
g(P,M)-гармон
в D
и непрерывно дифферен-я вплоть до
границы.3) ;
,
g(P,M)-гармон
в D
и непрерывно дифферен-я вплоть до
границы.3) ;
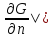 P∈S
=
P∈S
=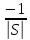 ,
|S|-
плотность поверх-ти
,
|S|-
плотность поверх-ти
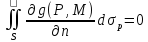 необх, чтобы
необх, чтобы
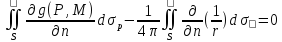 ;
получим 2ое слагаемое
;
получим 2ое слагаемое
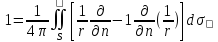 ;
;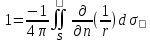 ;
;
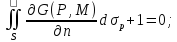
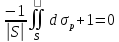 .
Используя ф-ю Грина, решение задачи
Неймана для ур-я Лапласа можно
представить:
.
Используя ф-ю Грина, решение задачи
Неймана для ур-я Лапласа можно
представить:
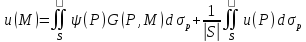
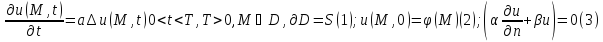 Т.
Реш задачи (1), (2), (3), непрер в заданной
области вместе со своими частн
производными 1го порядка, единств.
Док:
противное: сущ 2 реш задачи (1), (2), (3):
u1
и u2
. V
= u1-
u2
. V
– удовл однородной задаче.V|t
= 0 = 0
. Воспользуемся 1 ф-лой Грина, положив
u
= V.
Т.
Реш задачи (1), (2), (3), непрер в заданной
области вместе со своими частн
производными 1го порядка, единств.
Док:
противное: сущ 2 реш задачи (1), (2), (3):
u1
и u2
. V
= u1-
u2
. V
– удовл однородной задаче.V|t
= 0 = 0
. Воспользуемся 1 ф-лой Грина, положив
u
= V. Проинтегрируем
это рав-тво по t
от 0 до Т.В левой части подынтегральная
ф-ция неотриц, значит интеграл в левой
части
0, интегралы в правой части ≤ 0, значит
выражения равны 0.=> V
Проинтегрируем
это рав-тво по t
от 0 до Т.В левой части подынтегральная
ф-ция неотриц, значит интеграл в левой
части
0, интегралы в правой части ≤ 0, значит
выражения равны 0.=> V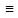 0 => u1
0 => u1
 u2
, значит
решение единственно.
u2
, значит
решение единственно.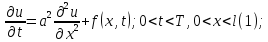 u(x,0)=
u(x,0)=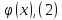 u(0,t)=μ1(t);
u(l,t)=μ2(t);
u(0,t)=μ1(t);
u(l,t)=μ2(t);
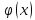 имеет кусочно непрер производную по
х.
имеет кусочно непрер производную по
х. .
Найдем все решения задачи
.
Найдем все решения задачи
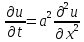 ;
u(0,t)=0;
u(l,t)=0;u(x,t)=X(x)T(t);
;
u(0,t)=0;
u(l,t)=0;u(x,t)=X(x)T(t);
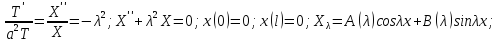 подставляем в граничные условия и
получаем,что A=0,
а
подставляем в граничные условия и
получаем,что A=0,
а
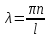 ;
;
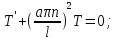
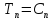 exp(-
exp(-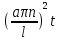 );
тогда общее реш:
);
тогда общее реш:
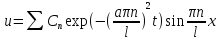 ;
найдем
;
найдем
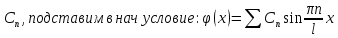 ;
;
 .Рассм
(1), (2),
(3)u(x,0)
= 0, f
C,
t
> 0 (2)f(0,t)
= f(l,
t)
= 0.f
– непрер и имеет кусочно-непрерывную
производную по t.
Будем искать решение задачи в виде:
.Рассм
(1), (2),
(3)u(x,0)
= 0, f
C,
t
> 0 (2)f(0,t)
= f(l,
t)
= 0.f
– непрер и имеет кусочно-непрерывную
производную по t.
Будем искать решение задачи в виде:
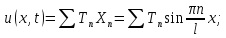 подставляем
в ур-ние:
подставляем
в ур-ние: ;
;
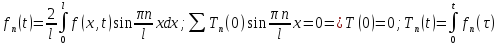 exp(-
exp(-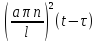 )dτ.
Тогда реш задачи:
)dτ.
Тогда реш задачи:
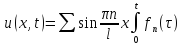 exp(-
exp(-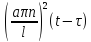 )dτ.
)dτ.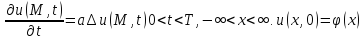 Из всех возможных условий на
бесконечности, будем рассм условие
ограниченности на бесконечности.
Из всех возможных условий на
бесконечности, будем рассм условие
ограниченности на бесконечности.
 .
Восп методом фурье разделения перем
.
Восп методом фурье разделения перем

 exp(-
exp(-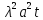 );
);
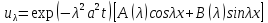 .
Так как
- произвольная, то если воспользоваться
всеми возможными ,
то
.
Так как
- произвольная, то если воспользоваться
всеми возможными ,
то
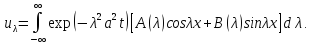 Это будет решением, если интеграл
равномерно сх-ся. Если функция
периодическая, то этот ряд определяет
ф-цию на всей числовой прямой.
Это будет решением, если интеграл
равномерно сх-ся. Если функция
периодическая, то этот ряд определяет
ф-цию на всей числовой прямой.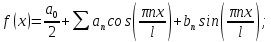
 .
f
.
f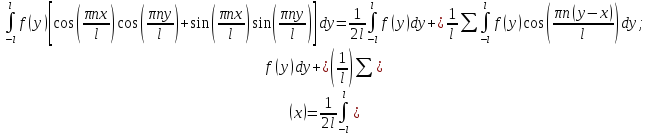
 ;
;
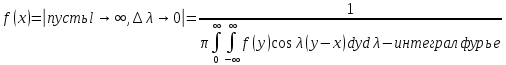 Подставим
наше реш в начал усл:
Подставим
наше реш в начал усл: .
Интеграл фурье для
.
Интеграл фурье для
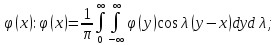
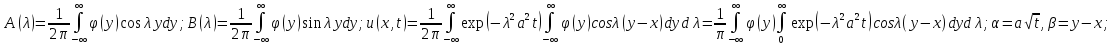 Подставим замену и получим:
Подставим замену и получим: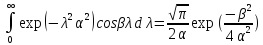 ;
;
 То
есть мы получили явный вид реш задачи
Коши. наз формулой Пуассона, интеграл
справа наз интегралом Пуассона.
То
есть мы получили явный вид реш задачи
Коши. наз формулой Пуассона, интеграл
справа наз интегралом Пуассона.

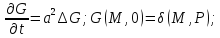
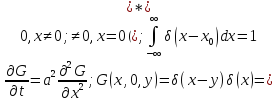 Построим
ф-цию Грина , восп формулой Пуассона:
Построим
ф-цию Грина , восп формулой Пуассона: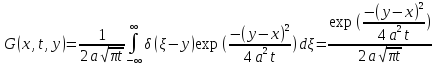 То
есть фундамент реш задачи Коши явл
ф-цией Грина.Будем считать, что в нек
момент времени участку [x0-h,x0+h]
сообщили количество тепла Q=2hcpUo,
где Uo-
показывает на сколько повысилась
температура. В этом случае ф-ла Пуассона:
То
есть фундамент реш задачи Коши явл
ф-цией Грина.Будем считать, что в нек
момент времени участку [x0-h,x0+h]
сообщили количество тепла Q=2hcpUo,
где Uo-
показывает на сколько повысилась
температура. В этом случае ф-ла Пуассона:
 .Уменьшаем
начал участок и стягиваем его к точке,
то есть h
0. Но ранее восп теоремой о среднем:
.Уменьшаем
начал участок и стягиваем его к точке,
то есть h
0. Но ранее восп теоремой о среднем:
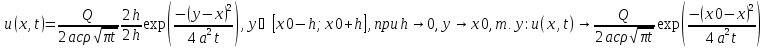 То
есть ф-ция Грина определяет распределение
температур в стержне в резул воздействия
мгновенного точечного источника.
То
есть ф-ция Грина определяет распределение
температур в стержне в резул воздействия
мгновенного точечного источника.
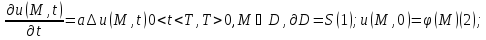 Л1.
Если
яв-тся нечетной относительно нуля, то
u(0,t)
Док. Решение задачи по формуле Пуассона
Л1.
Если
яв-тся нечетной относительно нуля, то
u(0,t)
Док. Решение задачи по формуле Пуассона
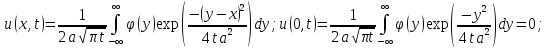 Лемма
2. Если в (1), (2) )
является четной относительно нуля,
то
Лемма
2. Если в (1), (2) )
является четной относительно нуля,
то
 Док.
Док.
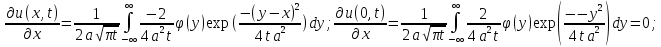 Р-м
след задачу:
Р-м
след задачу: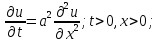 u(x,0)=
u(x,0)= u(0,t)=0
(6);
u(0,t)=0
(6);
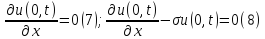 .Рассм
(1), (2), (6). Продолжим
нечетным образом. U(x,
t)
удовлетворяет задаче с
.Рассм
(1), (2), (6). Продолжим
нечетным образом. U(x,
t)
удовлетворяет задаче с
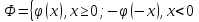 .
.
 Для
(1), (2), (7) :
Для
(1), (2), (7) :
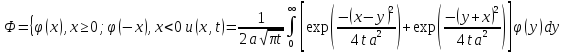
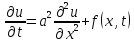 ;
U(M,t)=U(m);
;
U(M,t)=U(m);
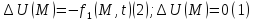 Опр.
Ф-ция
U(M)
наз гармонической в D
(конечная область с кусочно- гладкой
границей D
Опр.
Ф-ция
U(M)
наз гармонической в D
(конечная область с кусочно- гладкой
границей D ),
если она непрерыв со своими частн
произв до 2-го порядка и удовл ур-нию
Лапласа.Опр. Ф-ция U(M)
наз гармонической в неограниченной
области Е, если она непрерывна в Е
вместе со своими частными производными
до 2-го порядка , удовл ур-нию Лапласа
и убывает при стремлении
),
если она непрерыв со своими частн
произв до 2-го порядка и удовл ур-нию
Лапласа.Опр. Ф-ция U(M)
наз гармонической в неограниченной
области Е, если она непрерывна в Е
вместе со своими частными производными
до 2-го порядка , удовл ур-нию Лапласа
и убывает при стремлении
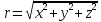 к
бесконечности, т.е.
к
бесконечности, т.е.
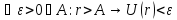 .
1.Пусть
D-
ограниченная область с кусочно-гладкой
границей, а Е- неограниченная область.
.
1.Пусть
D-
ограниченная область с кусочно-гладкой
границей, а Е- неограниченная область.
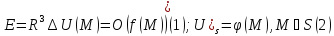 .
(1)(2)- задача Дирихле может быть внутр,
если решается в D,
внешней, если в E.
.
(1)(2)- задача Дирихле может быть внутр,
если решается в D,
внешней, если в E.
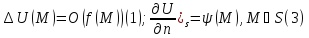 .(1)(3)
– задача Неймана, n-
внешняя нормаль к S.
.(1)(3)
– задача Неймана, n-
внешняя нормаль к S.
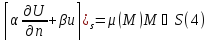 (1)(4) – 3я краевая задача.Пусть U
и V
явл непрерывными вместе со своими
частными производными вплоть до
второго порядка в D.
(1)(4) – 3я краевая задача.Пусть U
и V
явл непрерывными вместе со своими
частными производными вплоть до
второго порядка в D.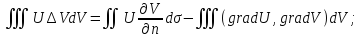 (5)– первая формула Грина.Аналогично
поменяв местами U
и V,
и вычитая это из (5) получим
(5)– первая формула Грина.Аналогично
поменяв местами U
и V,
и вычитая это из (5) получим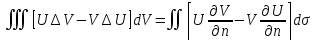 (6)-вторая формула Грина.
(6)-вторая формула Грина. R
+ ρ
≥ r
≥ R-ρ;
R
+ ρ
≥ r
≥ R-ρ;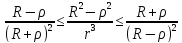 Умножим нер-во на u(P)
и проинтегрируем все части нер-ва на
сфере:
Умножим нер-во на u(P)
и проинтегрируем все части нер-ва на
сфере:
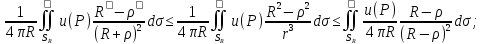 По Т о среднем:
По Т о среднем:
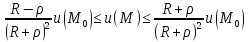 – нер-во Гарнака.
– нер-во Гарнака.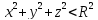 ;
U|x^2+y^2+z^2=R^2
= φ(M).
Построим ф-ю Грина для шара радиуса
R.
Выберем внутри шара произвольную
точку M(x,y,z)
. Проведем инверсию точки относительно
сферы и получим точку. |OM|=ρ,
|OM1|=ρ1
,ρρ1=R2
;
;
U|x^2+y^2+z^2=R^2
= φ(M).
Построим ф-ю Грина для шара радиуса
R.
Выберем внутри шара произвольную
точку M(x,y,z)
. Проведем инверсию точки относительно
сферы и получим точку. |OM|=ρ,
|OM1|=ρ1
,ρρ1=R2
;
 ;
;
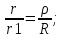
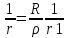 ;
ф-ю Грина можно представить
;
ф-ю Грина можно представить
 ;
;
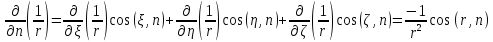 ;
;
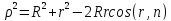 ;
cos(r,n)=
;
cos(r,n)=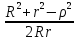 ;
; ;
(9) u(M)=
;
(9) u(M)=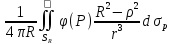 -
ф-ла Пуассона. Покажем, что правая
часть (9) удовлетворяет условию Лапласа.
При φ≡1 (9): 1=
-
ф-ла Пуассона. Покажем, что правая
часть (9) удовлетворяет условию Лапласа.
При φ≡1 (9): 1=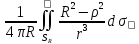 ;u(M)
- φ(N)=|M⟶N|=
;u(M)
- φ(N)=|M⟶N|=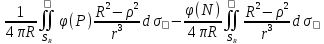 Проведем из выбранной точки N
шар радиуса 2δ
.
Проведем из выбранной точки N
шар радиуса 2δ
. -
часть поверхности SR,
попавшая в шар
-
часть поверхности SR,
попавшая в шар
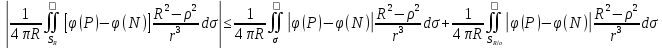 ;
|PN|<2δ
⇒|
φ(P)-φ(N)|<ε/2;
;
|PN|<2δ
⇒|
φ(P)-φ(N)|<ε/2;
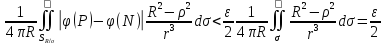 ,
|MN|≤δ;
,
|MN|≤δ;
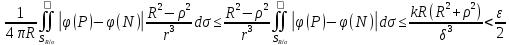 ; M⟶N⇒R2
- ρ2⟶0;
|u(M)-φ(N)|<ε.
Замеч: Решение внутренней задачи
Дирихле для круга описывается в виде
интеграла Пуассона:
; M⟶N⇒R2
- ρ2⟶0;
|u(M)-φ(N)|<ε.
Замеч: Решение внутренней задачи
Дирихле для круга описывается в виде
интеграла Пуассона: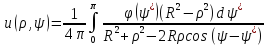 .
Внешняя задача Дирихле для шара:
∆u(M)=0
,
.
Внешняя задача Дирихле для шара:
∆u(M)=0
,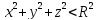 ;
U|x^2+y^2+z^2=R^2
= φ(M).
Решение задачи можно представить в
виде:
;
U|x^2+y^2+z^2=R^2
= φ(M).
Решение задачи можно представить в
виде:
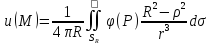 .
.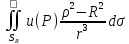 Из ∆ ОМР: R>ρ-r.Выберем
радиус сферы настолько большой если
ρ>2R,то
r>ρ/2
Из ∆ ОМР: R>ρ-r.Выберем
радиус сферы настолько большой если
ρ>2R,то
r>ρ/2
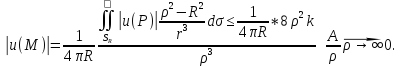
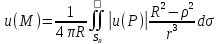
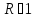 ,
|u(P)|<ε,
,
|u(P)|<ε,
 ,
|u(M)|<ε⇒u(M)≡0
,
|u(M)|<ε⇒u(M)≡0

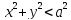 ;
U|x^2+y^2=a^2
=
;
U|x^2+y^2=a^2
= ;в
полярных: x=ρcosφ,
0≤ ρ ≤a,
y=
ρsinφ,
0≤ φ ≤2π;
u(x,y)
= u(ρ,φ);
;в
полярных: x=ρcosφ,
0≤ ρ ≤a,
y=
ρsinφ,
0≤ φ ≤2π;
u(x,y)
= u(ρ,φ);
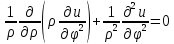 ;(1)
;(1)
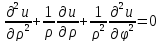 ;
(2) u(a,φ)=f(φ);
(3) u(ρ,φ+2πn)
= u(ρ,φ);
Найдем все нетривиальные реш (1),удовл
условию (3).U(ρ,φ)=R(ρ)Φ(φ);
;
(2) u(a,φ)=f(φ);
(3) u(ρ,φ+2πn)
= u(ρ,φ);
Найдем все нетривиальные реш (1),удовл
условию (3).U(ρ,φ)=R(ρ)Φ(φ);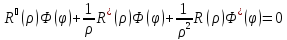 .Разделим
на u≢0
и
.Разделим
на u≢0
и
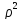 :
:
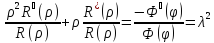 ;
;
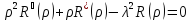 ;
;
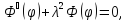
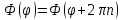 ;1)λ=0,
;1)λ=0,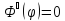 ,
,
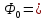 c1φ+c2
⇒
c1=0,
c1φ+c2
⇒
c1=0,
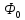 =c0=const;
2) λ≢0:
=c0=const;
2) λ≢0:
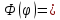 c1cosλφ
+ c2sinλφ,
λ=k=±1,±2;
c1cosλφ
+ c2sinλφ,
λ=k=±1,±2;
 ;
Введем замену: t=
lnρ
R(ρ)=y(t),
;
Введем замену: t=
lnρ
R(ρ)=y(t),
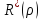 =
=
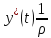 ,
,
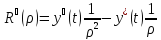 .
Подставим производные в уравнение:
.
Подставим производные в уравнение:
 ;
k=0:
;
k=0:
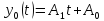 k
k 0:
0:
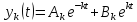 ;
;
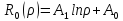 ,
,
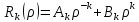 ;
;
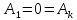 ;
;
;
;
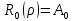 ;
;
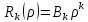 ;
;
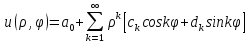 .
При ρ=A:
.
При ρ=A:
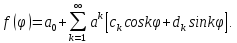
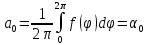 ;
;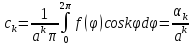 ;
;
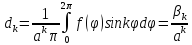 .
Решение внутренней задачи Дирихле
для круга принимает вид:
.
Решение внутренней задачи Дирихле
для круга принимает вид: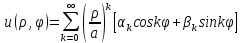 .
. Рассм.
когда М вне D.(N)
интегрируема в D.
Рассм.
когда М вне D.(N)
интегрируема в D. .При
удалении М от обл D
.При
удалении М от обл D
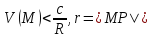 Р -произвольная точка, R
– расст от нач коорд.Поместим нач
коорд в точку О,
Р -произвольная точка, R
– расст от нач коорд.Поместим нач
коорд в точку О,
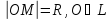 ,
d-диаметр
D.
,
d-диаметр
D.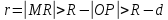 Бум считать, что М на столько удалена
от D,
что
Бум считать, что М на столько удалена
от D,
что
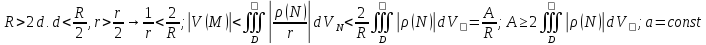 Обратим внимание, что
Обратим внимание, что
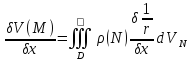 .Когда
МD,
V-
имеет непрерыв частн произв 1 порядка,
2 и т.д.
.Когда
МD,
V-
имеет непрерыв частн произв 1 порядка,
2 и т.д.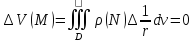 т.е. V-
непрер, имеет непрер частн произв,
удовлт уравнению Лапласа и стремится
на
т.е. V-
непрер, имеет непрер частн произв,
удовлт уравнению Лапласа и стремится
на
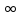 к 0, т.е. V
– гармонично вне D,
когда МD.Пусть
МD
если (N)<C
, то V-
непрерывна внутри D,
т.е. интеграл сходится равномерно во
внутр точках. Выделим
окрестность ()
то,
к 0, т.е. V
– гармонично вне D,
когда МD.Пусть
МD
если (N)<C
, то V-
непрерывна внутри D,
т.е. интеграл сходится равномерно во
внутр точках. Выделим
окрестность ()
то,
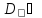 -
окрестности
-
окрестности

 ,т.о.
интеграл сходится равномерно в любой
внутр точке M0,
а отсюда являющейся U(M)
непрер, при МD.Теорема.
Если
,т.о.
интеграл сходится равномерно в любой
внутр точке M0,
а отсюда являющейся U(M)
непрер, при МD.Теорема.
Если
 - плотн объемного потенциала – огранич
в D,
то потенциал объема (1) является
функцией, непрерыв вместе с частными
производными 1 порядка во всем
пространстве. Эти производные могут
быть получены дифференц-ем под знаком
интеграла. Теор. Если плотность
объемного потенциала (N)
непрер в обл D
и непрер 1ые производные, то объемный
потенциал (1) в D
имеет непрер частные производные 2го
порядка и удовл внутри D
уравнению Пуассона. Замечание. Если
имеется уравнение Пуассона
- плотн объемного потенциала – огранич
в D,
то потенциал объема (1) является
функцией, непрерыв вместе с частными
производными 1 порядка во всем
пространстве. Эти производные могут
быть получены дифференц-ем под знаком
интеграла. Теор. Если плотность
объемного потенциала (N)
непрер в обл D
и непрер 1ые производные, то объемный
потенциал (1) в D
имеет непрер частные производные 2го
порядка и удовл внутри D
уравнению Пуассона. Замечание. Если
имеется уравнение Пуассона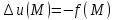 ,
то внутри D
это уравнение имеет частное решение
,
то внутри D
это уравнение имеет частное решение
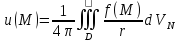 .
.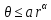 .Таким
образом второе условие обеспеч нам ,
чтобы z
= f(x,
y).
Третье условие обеспеч непрерывн
производных.В дальнейшем будем считать
все поверхности поверхностями
Ляпунова.Будем рассматривать потенциал
двойного слоя :
.Таким
образом второе условие обеспеч нам ,
чтобы z
= f(x,
y).
Третье условие обеспеч непрерывн
производных.В дальнейшем будем считать
все поверхности поверхностями
Ляпунова.Будем рассматривать потенциал
двойного слоя :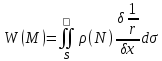 ,
,
 -прямое
значение, M=
-прямое
значение, M=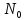 .MN0
изнутри или извне, и
.MN0
изнутри или извне, и
 предельное
внутр значение и если
равный конечный предел
предельное
внутр значение и если
равный конечный предел
 внешнее выделенное значение.Если
плотность потенциала двойного слоя
внешнее выделенное значение.Если
плотность потенциала двойного слоя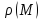 - непрерывна, то предельные значения
потенциала
и имеют место формулы.
- непрерывна, то предельные значения
потенциала
и имеют место формулы.
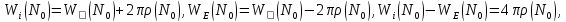 Замечание.
Потенциал двойного слоя равномерно
стремится к своим предельным значениям
изнутри и извне Теорема. Рассмотрим
потенциал простого слоя:Потенциал
простого слоя с непрерывной плотностью-
функция, непрерывная во всем пространстве.
Замечание.
Потенциал двойного слоя равномерно
стремится к своим предельным значениям
изнутри и извне Теорема. Рассмотрим
потенциал простого слоя:Потенциал
простого слоя с непрерывной плотностью-
функция, непрерывная во всем пространстве.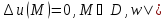 s=f(M),
M
s=f(M),
M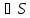 -
внутр.задача Дирихле. (2) )
-
внутр.задача Дирихле. (2) )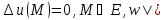 s=f(M),
M
s=f(M),
M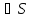 -внешняя
задача Дирихле (3) )
-внешняя
задача Дирихле (3) )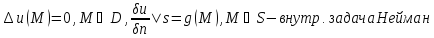 а,
(4)
а,
(4)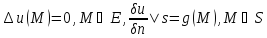 -внешн.задача
Неймана.Ищем решение задачи Дирихле
в виде потенциала двойного слоя с
неизв плотностью.
-внешн.задача
Неймана.Ищем решение задачи Дирихле
в виде потенциала двойного слоя с
неизв плотностью.
 для(1-2).Рассм.(1). Для того чтобы w
была реш задачи (1) необходимо: N0S.
для(1-2).Рассм.(1). Для того чтобы w
была реш задачи (1) необходимо: N0S.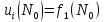 .
По теореме о разрывности потенциала
второго слоя можно
.
По теореме о разрывности потенциала
второго слоя можно
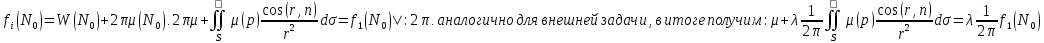 ,
,
 .
Для задач Неймана будем
искать
реш в виде потенциала простого слоя.
.
Для задач Неймана будем
искать
реш в виде потенциала простого слоя.
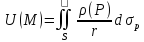 ,
,
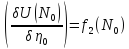 .
Получим
.
Получим
 ,для
,для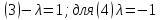 .
.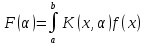 (1) называется интегральнымым
преобразованиемК(x,)
– ядро интеграла преобразования, а
[a,b]
интервалом интегрируемого преобразования.
(1) называется интегральнымым
преобразованиемК(x,)
– ядро интеграла преобразования, а
[a,b]
интервалом интегрируемого преобразования. (2), если имеется интеграл преобразования.Если
(2), если имеется интеграл преобразования.Если
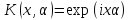 на
на
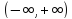 ,
то соответств интеграл преобразования
называется преобразованием Фурье.Если
,
то соответств интеграл преобразования
называется преобразованием Фурье.Если
 (3) это обозначение преобразования
Фурье.Если исходная функция f(r)
является интегрируемой на (-,
+)
(f(r)
L(-,
+))
и интеграл
(3) это обозначение преобразования
Фурье.Если исходная функция f(r)
является интегрируемой на (-,
+)
(f(r)
L(-,
+))
и интеграл
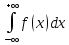 сходится
абсолютно (при этом
сходится
абсолютно (при этом
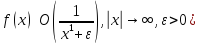 При
этом обращение преобразования Фурье
задается формулой.
При
этом обращение преобразования Фурье
задается формулой.
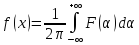 Св-ва преобраз Фурье.1.
Св-ва преобраз Фурье.1.
 2.
2.
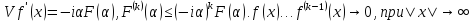 3.
3.
 .
4.
.
4.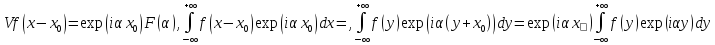 5.
5.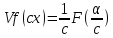 ,
,
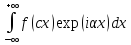 =
=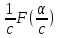
 ,
,
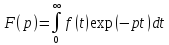 (1) преобраз Лапласа.
(1) преобраз Лапласа.
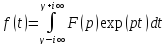 Где
Где
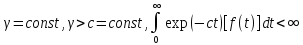 сх-ся. Отметим условия кот накладываются
на f(t)
как следствие из свойств F(p)1.
если F(p)
– анал ф-ция комплексной перем
сх-ся. Отметим условия кот накладываются
на f(t)
как следствие из свойств F(p)1.
если F(p)
– анал ф-ция комплексной перем
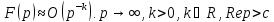 ,
то
,
то
 и
является преобразованием Лапласа,
для f(t)
такой, что f(t)
непрерывна
и
является преобразованием Лапласа,
для f(t)
такой, что f(t)
непрерывна
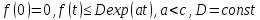 Если
функция имеет преобразования Лапласа,
то оно единственно.Если две функции
имеют одинаковые преобразования
Лапласа, то они различны на множестве
точек меры О. Пусть имеются две функции
f(t)
и g(t)
, t0,
и соответственно F(p)
и G(p)
– их преобразования Лапласа, то
справедливо соотношение:
Если
функция имеет преобразования Лапласа,
то оно единственно.Если две функции
имеют одинаковые преобразования
Лапласа, то они различны на множестве
точек меры О. Пусть имеются две функции
f(t)
и g(t)
, t0,
и соответственно F(p)
и G(p)
– их преобразования Лапласа, то
справедливо соотношение:

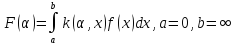 При
При
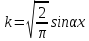 это преобразование называется
синус-преобразование Фурье.
это преобразование называется
синус-преобразование Фурье. (2)
– косинус-преобразование Фурьеf(x)
должна быть абсолютно интегрируемой
на [0, +)
Свойства преобразований Фурье на
полупрямой.
(2)
– косинус-преобразование Фурьеf(x)
должна быть абсолютно интегрируемой
на [0, +)
Свойства преобразований Фурье на
полупрямой.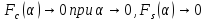 ;
;
 2.
2.
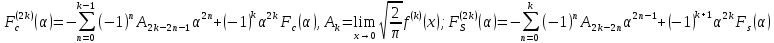
 -
соответствующие преобразования Фурье
функций f(x)
и g(x).
-
соответствующие преобразования Фурье
функций f(x)
и g(x).
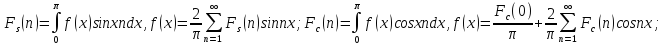 Пример.
Применим конечное преобразование
Фурье к задаче о колебании струны с
закрепл концами.
Пример.
Применим конечное преобразование
Фурье к задаче о колебании струны с
закрепл концами.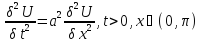 ,
,
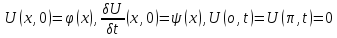 Обозн
Обозн
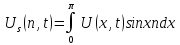 ,
,
 ,
,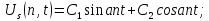 в
итоге:
в
итоге: