Teoria_chisel_i_kriptozashita

1. Определим z ≡ (ad + bc) (mod m), где 0 ≤ z < m. Тогда ad ≤ m,

bc ≤ m и ху ≡ (act + zT + bd) (mod m).

2. Пусть ac = eT + f, где 0 ≤ f < T. Тогда 0 ≤ е ≤ Т и xy ≡ ((et +

+z)T + ft + bd) (mod m).

3.Пусть v ≡ (z + et) (mod m), 0 ≤ v ≤ m.

4.Пусть v = gT + h, где 0 ≤ h < T. Тогда 0 ≤ g ≤ T и xy ≡ (hT + (f +

+g)t + bd) (mod m).

Представленные результаты просто проверить в такой последовательности ( все сравнения по модулю m):

a, b, c, d, z, e, f; v; g; h; j ≡ (f + g) t, k ≡ j + bd; xy ≡ hT + k,

включая числа размером не более 4m.

Для нахождения целых чисел в классах вычетов можно воспользоваться китайской теоремой об остатках

В кольце вычетов по модулю определены такие операции как сложение, вычитание, умножение, поэтому их выполнение осуществляется в соответствии с законами модулярной арифметики. Например, операцию мо-

дулярного вычитания чисел α и β можно осуществить в соответствии с выражением

(α – β) mod m = [α + (m – β)]mod m,

т.е. сводится к операции модулярного сложения.

Вычислительный процесс в модулярной системе счисления (МСС) отличает малоразрядность остатков, что позволяет использовать табличный метод для реализации арифметических операций. В этом случае остатки от деления операндов на модули системы счисления представляются однопозиционным кодом, и операции базового набора (сложение, вычитание и умножение) выполняются за один такт.

Под табличной реализацией функции двух входных переменных х = f(α, β) понимается создание такой таблицы, в которой каждой комбинации операндов α и β соответствует единственное значение выходной

переменной х (результата). При этом каждой паре операндов α и β соответствует определенный логический элемент табличного вычислителя, выходной сигнал которого шифруется в двоичные числа результата операции, соответствующие таблицам Кэли для модулярных операций базового набора. Недостатком табличного метода является существенный рост аппаратурных затрат при увеличении разрядности операндов.

Преобразования, требующие определенных видов арифметических вычислений, могут быть выполнены более просто в одной системе счисления, чем в другой. Следовательно, выбираемые кодер и декодер могут выполняться на основе различных алгоритмов преобразования.

31

2.5. Нахождение простых чисел

Простые числа выделяются с помощью тестирования какого либо выбранного целого числа на простоту.

Традиционными являются три метода получения простых чисел в возрастающем порядке: пробного деления, умножения для сокращения составных чисел и отсева (решета Эратосфена).

Простоту целого числа можно определять на основе теста Миллера, теста Пепина, малой теоремы Ферма, теоремы Вильсона и использования чисел Мерсенна.

Тест Миллера по основанию b. Если n нечётное положительное це-

лое число > 1, а b будет взаимно простым с n при условии выполнения следующей процедуры:

Шаг 1: Пусть k = n – 1, bk = r. Если r = 1, то продолжаем, в противном случае, n не выдерживает теста.

Пока k является чётным и r = 1, повторять следующее:

Шаг 2: Заменить k на k/2 и заменить r на новое значение bk . Когда k при проверке оказывается нечётным числом или r, не рав-

ным 1, то:

если r = 1 или n – 1, тогда n проходит тест,

если r ≠ 1 и r ≠ n – 1, тогда n не проходит тест.

Таким образом, как следует из проведенного выше обсуждения, если n — простое число и n не делит b (так что (b, n) = 1), тогда n всегда пройдёт тест Миллера по основанию b.

Решающим условием будет то, что х2 ≡ 1 (mod n), что предполагает х ≡ ±1 (mod n), когда n является простым числом, так что не может поя-

виться вычета другого, кроме ±1 (т.е. 1 или n – 1), а тест Миллера не сможет его отбросить. Конечно, шаг 1 точно соответствует малой теореме Ферма. Зарегистрируем этот факт следующим образом:

если тест Миллера даёт отрицательный результат по основанию b, тогда n — составное число.

Для чисел Ферма вида Fn = 22n +1 часто используется тест Пе-

пина на простоту. Предположим, что n ≥ 2 и k ≥ 2. Тогда, записывая F вместо Fn, получим, что следующие выражения эквивалентны:

а) F является простым числом и Fk = –1;

б) k(F-1)/2 ≡ –1 (mod F).

32

m — натуральное

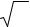
Теорема Вильсона. Целое число р > 1 является простым, если и

только если (р –1)! ≡ – 1 (mod p).

Доказательство. Предположим, что р — простое число большее 2. Мы должны умножить между собой все числа 1, 2, . . . , р – 1 и найти вычет по модулю р. Каждое из этих чисел х имеет обратное y по mod p, т.е., xy ≡ 1 (mod p). Далее мы должны все время сокращать y mod p, так что у станет одним из чисел 1, 2, . . . , р – 1. В этом случае имеем x = y x2 ≡ 1 (mod p) x ≡ ±1 (mod p), так как р – простое число. Другие числа разделены на пары, причем произведение каждой пары равно 1 mod p, так что 1 · 2 · 3 . . . (р – 1) ≡ –1 (mod p). Результат также верен и для р = 2!

С другой стороны, предположим, , что n — составное число, например, n = ab, где a > 1 и b > 1, а (n – 1)! ≡ –1 (mod n). Тогда получаем противоречие. Очевидно, что a | (n – 1)! для всех 1 < a < n. Но мы знаем, что a | n, так что их совпадение означает, что выражение a | (–1) является ложным.

Хотя теорема Вильсона в принципе даёт возможность тестировать на простоту, но для использования она достаточно малоэффективна, так как

для этого требуется умножение на все числа 2, 3, . . . . р – 1 по модулю p. Это получается медленнее, чем проверка р на принадлежность к простым числам путём пробного деления на простые числа ≤ p.

Числа Мерсенна имеют вид M(m) = 2m – 1, где число, большее единицы.

Совершенным числом считается такое целое n > 1, что сумма его делителей, включая 1, но исключая само число n, равно самому n.

Существует связь между совершенными числами и простыми числами Мерсенна.

Если известно разложение числа на простые множители, то можно указать все делители этого числа, а также найти их сумму, которую обо-

значим через σ(n), где n — само число. При этом для совершенных чисел

справедлива формула σ(n) = 2n.

Прежде чем выявить связь между совершенными числами и простыми числами Мерсенна, полезно описать метод, позволяющий определить,

является ли число вида M(m) = 2m – 1 действительно простым. Теорема. Пусть р будет нечётным простым числом, а q будет про-

стым числом. Предположим, что q | (2q – 1). Тогда q имеет вид 1 + 2kp для целого числа k. Все делители 2р – 1, простые или составные, будут иметь такой же вид.

33

Доказательство. Исходя из малой теоремы Ферма, q | (2q – 1), так что q | (2q – 1, 2р – 1) = 2(q--1,р) – 1. Отсюда (q – 1, p) = p вероятнее, чем

равенство 1. Это приводит к (q – 1) = rp, но р является нечётным, а (q – 1) является чётным, так что r должно быть чётным числом, скажем,

r = 2k. Из последнего утверждения следует, так как если q1 ≡ 1 и q2 ≡

≡ 1 (mod 2p), тогда q1 · q2 ≡ 1 (mod 2p).

Для примера выберем р = 31, что означает, что любой делитель чис-

ла (231 – 1) должен иметь вид (1 + 62k), так что простота числа 231 – 1 может быть проверена быстро путём пробного деления на числа этого специального вида.

Теорема о чётных совершенных числах. Если n является чётным совершенным числом, тогда существует m такое, что 2m – 1 является простым числом, а n = 2m-1 (2m – 1).

Доказательство. Предположим, что n является чётным совершенным числом и представимо как n = 2s t, где t является нечётным числом.

Тогда

2s+1t = 2n = σ(n) = σ(2s)σ(t) = (2s+1 – 1)σ(t),

так что 2s+1 | σ(t). Возьмем, скажем, σ(t)= 2s+1q. Продолжим далее, чтобы показать, что q = 1.

Предположим, что q > 1, так что t = (2s+1 – 1)q, Тогда q является собственным множителем t, a t имеет различные множители 1, q, t (и, воз-

можно, другие), обеспечивая σ(t) ≥ 1 + q + t, С другой стороны,

σ(t) = 2s+1q = (2s+1 – 1)q + q = t + q.

Это противоречие доказывает, что q = 1, обеспечивая t = 2s+1 – 1, и σ(t) = 1 + t. Последнее уравнение показывает, что t — простое число, так что n = 2s(2s+1 – 1), где второй сомножитель является простым.

Таким образом, существует тесная связь между чётными совершенными числами и простыми числами Мерсенна. Значения m, при которых число становится простым, сами все являются простыми. Приведем несколько первых простых чисел Мерсенна при m = 2, 3, 5, 7, 13, 17, 19,

31, 61, 89, 107, 127,521, 607, 1279, 2203, 2281, 3217, 4253, . . .

При разложении составного числа на нечетные простые множители часто используют числа Кармайкла.

Числом Кармайкла называется составное число n, которое удовлетворяет сравнению bn-1 ≡ 1 (mod n) для всех b, являющихся взаимно про-

стыми с n (в честь Р. Д. Кармайкла, который предложил их в 1912 г.). Конечно, давая определение, мы не доказали, что такие числа суще-

ствуют, но приведём пример. Пусть n = 561 = 3 · 11 · 17. Таким образом,

34

k K ; множество

(b, 561) = 1 означает, что (b, 3) = (b, 11) = (b, 17) = 1. Используя ма-

лую теорему Ферма,

b2 ≡ 1 (mod 3) предполагает, что b 560 = (b2)280 ≡ 1 (mod 3); b10 ≡ 1 (mod 11) означает, что b560 = (b10)56 ≡ 1 (mod 11); b16 ≡ 1 (mod 17) означает, что b560 = (b16)35 ≡ 1 (mod 17).

Так как 3, 11 и 17 являются тремя различными простыми числами, то это означает, что b560 ≡ 1 (mod 561).

Теорема. Пусть n = q1 q2 . . . qk, где qi — различные простые числа

и k ≥ 2. Предположим, что для каждого i, (qi – 1) | (n – 1). Тогда n будет числом Кармайкла.

Заметим, что простые числа должны быть нечётными, так как, если q1 = 2, тогда n — чётное, а q2 , будучи нечётным, не удовлетворяет усло-

вию (q2 – 1) | (n – 1).

3. Формальное определение криптосистемы

Наряду с определением, приведенным ранее, криптосистемой называют совокупность ∑A ={X , K,Y , E, D} множеств, для которых выпол-

няются следующие свойства [5] :

1) для любых x X и k K выполняется равенство

Dk (Ek (x)) = x ;

2) Y = Ek (X ) .

k K

Здесь: X , Y , K — конечные множества возможных открытых текстов, шифрованных текстов и ключей соответственно;

Ek : X →Y — правило зашифрования на ключе

{Ek :k K} = E , а множество {Ek (x) :x X} = Ek (X ) ;

Dk :Ek (X ) → X — правило расшифрования на ключе k K , и

D ={Dk :k K};

Обычно предполагают, что если k K представляется в виде k = (ko ;ks ) , где ko – открытый ключ для зашифрования информации, а

ks — секретный ключ для расшифрования (причем ks ≠ ko ), то Ek понимается как функция Eko , а Dk — как функция Dks .

Условие 1 отвечает требованию однозначности расшифрования

(принцип обратимости).

Условие 2 означает, что любой элемент y Y может быть представлен в виде y = Ek (x) для подходящих x X и k K . Отметим также,

35

что в общем случае утверждение «для любых k K и y Ek (X ) выполняется равенство Ek (Dk ( y)) = y » является неверным.

Совокупность множеств ∑A — алгебраическая модель шифра.

4. Криптосистема Эль Гамаля [3—5]

Определение. Целое x, удовлетворяющее сравнению ax ≡ b(mod n),

называется дискретным логарифмом числа b по модулю n и по основанию a .

Криптосистема Эль Гамаля была предложена в 1985 году американцем арабского происхождения Тахер Эль Гамалем. Данная система бази-

руется на сложности решения задачи дискретного логарифмирования, то есть определении числа x при известных параметрах a , b и n

в сравнении ax ≡ b(mod n).

В соответствии с алгебраической моделью шифра ∑A ={X , K,Y , E, D} шифрсистема Эль Гамаля определяется следующим

образом.

Обозначим: Z p ={0;1;2;...;( p −1)} — множество чисел, представляющее собой полную систему вычетов для некоторого простого числа p ;

Z*p — множество обратимых	элементов совокупности Z p ;		X = Z*p ,
Y = Z*p ×Z*p , K = {( p , α , β , δ ) :α δ		≡ β (mod p )} , где	p — дос-
таточно большое простое число ( ~ 10308		или ~ 21024 ); α — большое це-
лое число ( ~ 10154 или ~ 2512 );	δ — случайное целое число из интерва-
ла 1 ≤δ ≤ ( p −2).
k = (ko ;ks ) ; ko = ( p,α, β)	— открытый ключ; ks = (δ) — секрет-

ный ключ.

Правило зашифрования определяется следующей формулой:

Eko (M ) = (C1; C2 ), где M — открытый текст; (C1; C2 ) — шифр. C 1 ≡ α r (mod p ) ; C 2 ≡ ( M β r )(mod p) ; r — рандомиза-

тор — случайное целое число из интервала 1 ≤ r ≤ ( p −2), необходимое

для реализации схемы вероятностного шифрования, при которой зашифрование одинаковых блоков открытого текста будет давать различные шифрованные тексты (открытый текст и ключ не определяют шифрованный текст однозначно).

36

Правило расшифрования:
D k s (C1 , C 2 ) = (C 2 (C1δ ) −1 ) mod							p .
Замечание. При расшифровании используется секретный ключ δ и не
используется рандомизатор r .
Доказательство корректности алгоритма Эль Гамаля
Требуется доказать выполнимость условия обратимости:
		D k s (C1 , C 2 ) = M .
Действительно [5] : D	k s	(C	1	, C	2	) = {[( M β r ) mod	p ]

{[(αrδ mod p)−1]mod p}}mod p = [M α rδ (α rδ )−1 ]mod p = M .

Здесь учтено, что M < p и [αrδ (αrδ )−1]mod p =1.

Необходимость использования различных значений рандомизатора r

для различных открытых					текстов	M и		M *	подтверждается тем, что в
противном				случае	соответствующие				шифрованные	тексты
(C ;C	2	) = E	ko	(M ) и	(C*;C*) = E		ko	(M *)	связаны соотношением
1					1 2

C2 (C2*)−1 = M (M *)−1 , т.е. открытый текст M * может быть вычислен

по известному M.

Так как криптостойкость системы Эль Гамаля определяется сложностью решения задачи дискретного логарифмирования в совокупности Z*p , то следует учесть, что в настоящее время эта задача неразрешима при p , содержащем примерно 300 десятичных цифр. Рекомендуется также, чтобы число ( p −1) содержало большой простой делитель.

Вероятностный характер шифрования может быть отнесен к достоинствам системы Эль Гамаля, такие схемы обладают, как правило, большей криптостойкостью, чем детерминированные алгоритмы.

Недостатком системы является удвоение длины шифрованного текста по отношению к открытому тексту.

5. Криптосистема RSA (R. Rivest, A. Shamir, L. Adleman)

Наиболее широкое признание и применение в современном мире получила схема шифрования с открытым ключом RSA, аббревиатура которого исходит от фамилий авторов Р. Л. Ривеста, А. Шамира и Л. М. Адлемана. Основой надёжности этого метода является огромная трудность факторизации очень больших целых чисел. Метод также требует использования очень больших простых чисел (150-значных и более), которые практически находятся вероятностными методами, подобными изложенным ранее.

37

Основы создания криптосистемы RSA, рассматриваемой далее, берут своё начало из экспоненциального шифрования [10]. Они были открыты С. Полигом и М. Хэллманом [9;10]. Идея довольно проста. Выбирается про-

стое число р и ключ кодирования е, который является взаимно простым с ϕ( p) = p −1. Блок открытого текста, который предполагается зашифро-

вать, сначала преобразуется в числовую форму (один из методов осуществления этого приведён ниже), а потом разбивается на подблоки цифр, ко-

торые, если рассматривать их как обычные числа, будут < р. Предположим, например, что р = 37 781, а подблоки цифр сообще-

ния в числовом виде выглядят как

8069 6578 8584 8332.

Чтобы зашифровать это послание, заменим каждое четырёхзначное число Mi (существующее «открытым текстом» в виде четырёхзначных чисел) на Ci ≡ Mie (mod p), 0 < Ci < p. Таким образом, выбирая е = 367 (ко-

торое является взаимно простым числом с р – 1 = 37 780 = 22 · 5 ·1889), зашифрованной формой будет

37059 12498 22955 20254

(т. е. 8069367 ≡ 37 059 (mod p)).

Как может быть это послание расшифровано, т.е. возвращено к первоначальной цифровой форме и, далее, к обычному языку? Пусть d (ключ расшифрования) будет таким, что de ≡ 1 (mod( p – 1)). То есть d просто

представляет собой инверсию е по модулю (p – 1), так как (е, р – 1) = 1, и которая может быть вычислена методами определения обратных по моду-

лю величин . В представленном случае d = 3603. Теперь

Cid = (Mie) d = Mied = (Mied-1)·Mi = Mi mod p

согласно малой теореме Ферма, так как (p – 1) | (ed – 1). Таким образом, возводя каждое (пятизначное) зашифрованное число в степень d и приводя

по mod p, мы раскроем первоначальное (четырёхзначное) число. То есть

(37 0593603) mod p = 8069 и т. д.

Чтобы использовать этот метод для отправки секретных посланий между двумя людьми А и В, которые оба желают знать р (вся шифрация производится по модулю p), А необходимо выбрать шифровальный ключ е, в то время как В должен произвести соответствующую расшифровку

ключом d. Конечно, В может выбрать другой шифровальный ключ е′ для отправки посланий А, так как А знает соответствующий ключ расшифровки d′, для которого d′e′ ≡ 1 (mod (p – 1)).

Раскрытие этого шифра достаточно сложно, даже если р известно и если соответствующие открытый текст M и зашифрованный текст С известны, так что C ≡ M e (mod p). Проблема заключается в том, что не су-

38

ществует простого способа определения е из такого сравнения, когда р представляет большое простое число.

Если простое число р и ключ шифрования (экспоненциального) е являются оба раскрытыми в экспоненциальном шифровании, тогда, конечно, всё потеряно (или найдено): ключ расшифрования может быть просто найден как инверсия е по модулю р – 1. Метод криптографии с открытым ключом является искусным способом посылки секретных сообщений между двумя (или другим каким-либо числом) людьми, даже когда ключи шифрования открыты (отсюда название), потому что нахождение ключей для расшифрования является вычислительно трудной задачей.

Сама идея достаточно проста. Если два абонента сети, которых обозначим А и В, соответственно, хотят установить скрытую связь, каждый

выбирает два больших простых числа: pR, qR и pG, qG. Пусть nR = pR qR , nG = pG qG. Числа nR и nG могут быть известны окружающим, так как используемые простые числа достаточно большие. Каждый выбирает ключ шифрования: еR и еG, каждый из которых будет взаимно простым с ϕ(nR ),

ϕ(nG ), соответственно. (Заметим, что ϕ( pq) = ( p −1)(q −1) , когда p и q являются простыми). Эти шифровальные ключи могут также быть известны окружающим. Каждый человек, знающий свои р, q и е, может просто рассчитать инверсию d для е по модулю ϕ(n) . Но посторонний человек, знающий только n и е, имеет незначительный шанс вычислить d без действительного разложения на простые сомножители n, а А реально не в состоянии вычислить dG, а В не сможет определить dR.

Когда А захочет послать сообщение В, он преобразует его обычным способом в числовые блоки. Он также использует шифровальный ключ В

еG (который, как все шифровальные ключи, общеизвестен), чтобы зашифровать каждый блок Р в соответствии с правилом шифрования EG:

ЕG (Р) ≡ РеG (mod nG ).

Заметим, что, выполнив это шифрование, А будет не в состоянии расшифровать его снова, так как он не знает dG. Однако В будет находиться не в таком безнадёжном положении: зная оба dG и nG, он сможет расшифровать с помощью правила расшифрования:

DG (С) ≡ СdG (mod nG ).

Таким образом, DG (ЕG(Р)) ≡ Р (mod nG) на основе тех же самых аргументов, какие были использованы в случае экспоненциального шифрования.

Конечно, когда В пожелает отправить послание R, он использует правило шифрования

39

ЕR (Р) ≡ РеR (mod nR ),

а А расшифрует согласно правилу расшифровки DR (С) ≡ Сd R (mod nR ) . Снова DR (ЕR(Р)) ≡ Р (mod nR). Вспомните, что А знает ER, EG и

DR, в то время, как В знает ER, EG и DG .

Важной частью написанного послания является подпись, чью индивидуальность подтверждает получатель тем, что сообщение действительно получено от персоны, которую затребовал отправитель. Удивительно, что возможно послать подпись, используя также открытый метод RSA шифро-

вания. Предположим, что nR < nG (конечно, оба А и В знают об этом) и то, что А желает послать подпись В, т. е. последовательность символов в конце послания, которую В должен сделать, чтобы раскрыть смысл послания, которое могло бы прийти только от А. Предположим, что в действительности подпись представляет собой один блок открытого текста Р. Тогда А зашифровывает его с помощью представления DR(P) в меньших блоках перед дальнейшим шифрованием его как S. В конце этого сообщения А тогда посылает подпись S. Когда получатель В расшифрует конец послания, используя ключ расшифрования dG , получается настоящая тарабарщина,

а именно:

DG (S) = DG (EG(DR(P))) = DR (P)

(конечно, DR(P) является числом). Бессмыслица получится, когда В будет стремиться превратить эти числа в слова. Предполагая, что это является подписью, он для этого используетЕR , которое раскрывает В; когда оно переводится в слова, то приобретает смысл. Заметим, что только отправитель А знает DR, так что только он может послать специфическую тарабарщину DR в конце послания.

Доказательство корректности алгоритма RSA [5]

Определение. Пусть n = p q , где p и q — простые числа. Пусть X =Y = Zn –– множество открытых текстов, которое по объему сов-

падает с множеством шифрованных текстов и равняется полной системе вычетов по модулю n.

Предположим, что ключевое пространство имеет вид
K ={(n, p, q,e, d) : e, d Zn , n = p q, e d ≡1(modϕ(n))},		где
ϕ( ) — функция Эйлера, (e,ϕ(n)) =1. Представим ключ	k K в виде
k = (ko ;ks ) , где ko = (n,e) — открытый ключ; ks = (d)	— секретный
ключ.

40