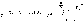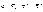- •11.Вероятность появления хотя бы одного события.
- •32. Понятие двумерной случайной величины и закон ее распределения.
- •45.Выборочная дисперсия и ее свойства;
- •48.Точечная оценка математического ожидания
- •49.. Точечная оценка для дисперсии
- •50. Несмщенная точечная оценка генеральной совокупности.
- •53. Интервальная оценка мат.Ожидания
- •56- Методика проверки статистических гипотез
- •57. Критерий согласия Пирсона
- •58. Критерий согласия Колмагорова
- •59. Системы массового обслуживания.
- •60. Основные понятия теории графов.
1.В
комбинаторике изучают вопросы о том,
сколько комбинаций определенного типа
можно составить из данных предметов.раздел
математики, изучающий дискретные
объекты, множества и отношения на
них.Перестановки.Пусть
имеется n различных объектов. Будем
переставлять их всеми возможными
способами (число объектов остается
неизменными, меняется только их порядок).
Получившиеся комбинации называются
перестановками, а их число равно
перестановки, формулы
комбинаторики.Pn=n!=1⋅2⋅3⋅...⋅(n−1)⋅n
(0!=1,1!=1)

Размещения.размещения,
формулы комбинаторики.Пусть имеется
n различных объектов. Будем выбирать
из них m объектов и переставлять всеми
возможными способами между собой (то
есть меняется и состав выбранных
объектов, и их порядок). Получившиеся
комбинации называются размещениями
из n объектов по m, а их число равно
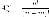 Сочетания.Пусть
имеется n различных объектов. Будем
выбирать из них m объектов все возможными
способами (то есть меняется состав
выбранных объектов, но порядок не
важен). Получившиеся комбинации
называются сочетаниями из n объектов
по m, а их число равно
Сочетания.Пусть
имеется n различных объектов. Будем
выбирать из них m объектов все возможными
способами (то есть меняется состав
выбранных объектов, но порядок не
важен). Получившиеся комбинации
называются сочетаниями из n объектов
по m, а их число равно
2.
Событием называется любой факт, который
в результате опыта может произойти или
не произойти. Достоверным называется
событие W, которое происходит в каждом
опыте.Невозможным называется событие
Æ , которое в результате опыта произойти
не может.Несовместными называются
события, которые в одном опыте не могут
произойти одновременно.
Суммой двух
событий A и B называется
такое событие, которое заключается в
том, что происходит хотя бы одно из
событий.Произведением двух
событий A и B называется
такое событие, которое заключается в
том, что происходят оба
события A и B вместе.Противоположным к
событию A называется
такое событие 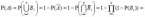 ,
которое заключается в том, что событиеA не
происходит.Разностью
событий
А и В называется событие С, состоящее
в том, что А происходит, а В не происходит
и обозначается А \ В События Ak (k=1,
2, ..., n)
образуют полную
группу,
если они попарно несовместны и в сумме
образуют достоверное событие.
,
которое заключается в том, что событиеA не
происходит.Разностью
событий
А и В называется событие С, состоящее
в том, что А происходит, а В не происходит
и обозначается А \ В События Ak (k=1,
2, ..., n)
образуют полную
группу,
если они попарно несовместны и в сумме
образуют достоверное событие.
3.
Вероятностью
события A называют
отношение числа m благоприятствующих
этому событию исходов к общему числу
n всех равновозможных несовместных
элементарных исходов, образующих полную
группу.Наблюдение явления, опыт,
эксперимент, которые можно провести
многократно, в теории вероятностей
принято называть испытанием. Результат,
исход испытания называется
событием.
Свойство
1. Вероятность
достоверного события равна единице
Свойство
2. Вероятность
невозможного события равна нулю.
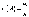 Свойство
3. Вероятность
случайного события есть положительное
число, заключенное между нулем и
единицей.
Относительной
частотой события А называют
отношение числа испытаний, в которых
событие появилось, к общему числу
фактически произведенных испытаний:
Свойство
3. Вероятность
случайного события есть положительное
число, заключенное между нулем и
единицей.
Относительной
частотой события А называют
отношение числа испытаний, в которых
событие появилось, к общему числу
фактически произведенных испытаний:
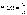
где m – число появлений события А, n – общее число испытаний.Классическая вероятность вычисляется до опыта, а относительная частота – после опыта.Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число и есть вероятность появления события.Таким образом, при достаточно большом количестве испытаний в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.
4.
Геометрическая вер-ть. Чтобы преодолеть
недостаток классического определения
вероятности, состоящий в том, что оно
неприменимо к испытаниям с бесконечным
числом исходов, вводят геометрические
вероятности — вероятности попадания
точки в область (отрезок, часть плоскости
и т. д.).Пусть случайное испытание можно
представить себе как бросание точки
наудачу в некоторую геометрическую
область G (на прямой, плоскости или
пространстве). Элементарные исходы –
это отдельные точки G, любое событие –
это подмножество этой области,
пространства элементарных исходов G.
Можно считать, что все точки G «равноправны»
и тогда вероятность попадания точки в
некоторое подмножество пропорционально
его мере (длине, площади, объему) и не
зависит от его расположения и
формы.Геометрическая
вероятность события
А определяется отношением:
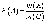 , где
m(G), m(A) – геометрические меры (длины,
площади или объемы) всего пространства
элементарных исходов и события А.
, где
m(G), m(A) – геометрические меры (длины,
площади или объемы) всего пространства
элементарных исходов и события А.
5.
Теорема
сложения для совместных соб-й.
События А и В называют совместными,
если в одном и том же испытании
появление одного из них не исключает
появления другого.Вероятность появления
хотя бы одного из совместных событий
равна сумме вероятностей этих событий
минус вероятность их совместного
появления: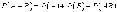
6. Теорема сложения для несовместных событий: вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:Р (А + В) = Р (А) + Р (В).ДоказательствоС л е д с т в и е.Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:Р (A1 + A2 + ... + An) = Р (A1) + Р (A2) + ... + Р (An).Рассмотрим три события: А, В и С. Так как рассматриваемые события попарно несовместны, то появление одного из трех событий, А, В и С, равносильно наступлению одного из двух событий, A + В и С, поэтому в силу указанной теоремыР ( А + В + С) = Р [(А + В) + С] = Р (А + В) + Р (С) = Р (А) + Р (В) + Р (С).
7.
Условная вероятность событий. Случайное
событие определено как событие, которое
при осуществлении совокупности условий
эксперимента может произойти или не
произойти. Если при вычислении вероятности
события никаких других ограничений,
кроме условий эксперимента, не налагается,
то такую вероятность называют безусловной;
если же налагаются и другие дополнительные
условия, то вероятность события
называют условной.
Например, часто вычисляют вероятность
события В при
дополнительном условии, что произошло
событие А.Условной
вероятностью 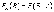
(два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.
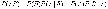 .В
частности, отсюда получаем
.В
частности, отсюда получаем
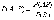 .Предположим, что
по статистике вероятность того, что
человек доживает до 80 лет
.Предположим, что
по статистике вероятность того, что
человек доживает до 80 лет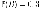 ,
а вероятность того, что человек доживет
до 90 лет
,
а вероятность того, что человек доживет
до 90 лет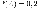 Какова
вероятность того, что человек доживший
до 80 лет доживет до 90?
Какова
вероятность того, что человек доживший
до 80 лет доживет до 90?
Решение:
 (если
независимы)но так как вероятности
зависимы, то пересечение вероятности
будет 0,2
(если
независимы)но так как вероятности
зависимы, то пересечение вероятности
будет 0,2
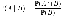 0,2/0,3
= 2/3 ≈ 0,67
0,2/0,3
= 2/3 ≈ 0,67
8.
Зависимые
и независимые события.
Два события называются независимыми,
если появление одного из них не изменяет
вероятность появления другого. Например,
если в цехе работают две автоматические
линии, по условиям производства не
взаимосвязанные, то остановки этих
линий являются независимыми событиями.
Несколько
событий называются независимыми
в совокупности,
если любое из них не зависит от любого
другого события и от любой комбинации
остальных.События
называются зависимыми,
если одно из них влияет на вероятность
появления другого. Например, две
производственные установки связаны
единым технологическим циклом. Тогда
вероятность выхода из строя одной из
них зависит от того, в каком состоянии
находится другая. Вероятность одного
события  ,
вычисленная в предположении осуществления
другого события
,
вычисленная в предположении осуществления
другого события ,
называетсяусловной
вероятностью события
,
называетсяусловной
вероятностью события  и
обозначается
и
обозначается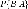 .
.
Условие
независимости события  от
события
от
события записывают
в виде
записывают
в виде ,
а условие его зависимости — в виде
,
а условие его зависимости — в виде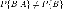
9.
Теоремы умножения для независимых
случайных событий. Пусть
события  и
и независимые,
причем вероятности этих событий
известны. Найдем вероятность
совмещениясобытий
независимые,
причем вероятности этих событий
известны. Найдем вероятность
совмещениясобытий и
и .Теорема
2.3. Вероятность
совместного появления двух независимых
событий равна произведению вероятностей
этих событий:
.Теорема
2.3. Вероятность
совместного появления двух независимых
событий равна произведению вероятностей
этих событий: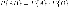
Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
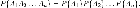
10.
Вероятность совместного появления
двух зависимых событий равна произведению
вероятности одного из них на условную
вероятность другого, вычисленную в
предположении, что первое событие
уженаступило: Следствие
2.2. Вероятность
совместного появления нескольких
зависимых событий равна произведению
вероятности одного из них на условные
вероятности всех остальных, причем
вероятность каждого последующего
события вычисляется в предположении,
что все предыдущие события уже появились.
Следствие
2.2. Вероятность
совместного появления нескольких
зависимых событий равна произведению
вероятности одного из них на условные
вероятности всех остальных, причем
вероятность каждого последующего
события вычисляется в предположении,
что все предыдущие события уже появились.
11.Вероятность появления хотя бы одного события.
Вероятность наступления события А, состоящего в появлении хотя бы одного из событий А1, А2,..., Аn,независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
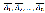
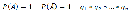
Ч а с т н ы й с л у ч а й. Если события А1 , А2 , ..., Аn имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий
P (A) = l — qn.
12. Формула полной вероятности и формула Байеса
Если
событие А может
произойти только при выполнении одного
из событий 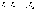 ,
которые образуютполную
группу несовместных событий,
то вероятность события А
вычисляется
по формуле
,
которые образуютполную
группу несовместных событий,
то вероятность события А
вычисляется
по формуле
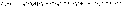 .Эта
формула называется формулой
полной вероятности.
.Эта
формула называется формулой
полной вероятности.
Вновь
рассмотрим полную группу несовместных
событий 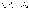 ,
вероятности появления которых
,
вероятности появления которых .
СобытиеА может
произойти только вместе с каким-либо
из событий
.
СобытиеА может
произойти только вместе с каким-либо
из событий 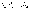 ,
которые будем называтьгипотезами.
Тогда по формуле полной вероятности
,
которые будем называтьгипотезами.
Тогда по формуле полной вероятности
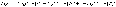
Если
событие А произошло,
то это может изменить вероятности
гипотез 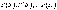 .
.
По теореме умножения вероятностей
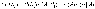 ,
,
откуда .
.
Аналогично, для остальных гипотез

Полученная
формула называется формулой
Байеса (формулой
Бейеса).
Вероятности гипотез  называютсяапостериорными
вероятностями,
тогда как
называютсяапостериорными
вероятностями,
тогда как 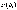 -априорными
вероятностями
-априорными
вероятностями
13. независимые испытания. Формула Бернулли
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний илисхемой Бернулли.
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е. p=P(A), а вероятность противоположного события (событие А не наступило) - буквой q=P(A¯¯¯)=1−p.
Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражаетсяформулой Бернулли

где 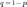 .
.
Так
как рассматривалась только одна из
возможных комбинаций, когда
событие  произошло
только в первых
произошло
только в первых  испытаниях,
то для определения искомой вероятности
нужно перебрать все возможные комбинации.
Их число будет равно числу сочетаний
из
испытаниях,
то для определения искомой вероятности
нужно перебрать все возможные комбинации.
Их число будет равно числу сочетаний
из  элементов
по
элементов
по  ,
т.е.
,
т.е. 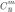 .
.
Таким
образом, вероятность того, что
событие  наступит
ровно в
наступит
ровно в  испытаниях
определяется по формуле
испытаниях
определяется по формуле
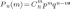 ,
(3.3)
,
(3.3)
где  .
.
14. Пуассон
Теорема. Если
вероятность  наступления
события
наступления
события в
каждом испытании постоянна и мала, а
число независимых испытаний
в
каждом испытании постоянна и мала, а
число независимых испытаний достаточно
велико, то вероятность наступления
события
достаточно
велико, то вероятность наступления
события ровно
ровно раз
приближенно равна
раз
приближенно равна
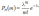 ,(3.4)
,(3.4)
где  .
.
Доказательство. Пусть
даны вероятность наступления события  в
одном испытании
в
одном испытании и
число независимых испытаний
и
число независимых испытаний .
Обозначим
.
Обозначим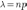 .
Откуда
.
Откуда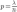 .
Подставим это выражение в формулу
Бернулли:
.
Подставим это выражение в формулу
Бернулли:
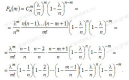
При достаточно большом !!n,, и сравнительно небольшом !!m,, все скобки, за исключением предпоследней, можно принять равными единице, т.е.
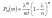
Учитывая
то, что  достаточно
велико, правую часть этого выражения
можно рассмотреть при
достаточно
велико, правую часть этого выражения
можно рассмотреть при ,
т.е. найти предел
,
т.е. найти предел
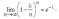
Тогда получим
 (3.5)
(3.5)
15,16 .Локальная и интегральная теоремы Лапласа.В схеме Бернулли распределение вероятностей - биномиальное. При большом количестве проводимых испытаний биномиальное распределение приближается к нормальному с параметрами a = np, σ = √(npq). На этом факте и основано применение приближённых формул Лапласа. Условия применения формул - схема Бернулли (проводимые испытания независимы, вероятность наступления события в каждом испытании постоянна). Тогда вероятность того, что при n испытаниях интересующее нас событие наступит ровно k раз (безразлично, в какой последовательности), приближённо равна
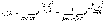
17. понятие случайной величины. дискретные и непрерывные случайные величины
Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Выпадение некоторого значения случайной величины Х это случайное событие: Х = хi. Среди случайных величин выделяют дискретные и непрерывные случайные величины.
|
x1 |
x2 |
… |
xn |
|
p1 |
p2 |
… |
pn |
Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют.
Случайная величина (непрерывная или дискретная) имеет численные характеристики:
Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.
Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.
Среднее квадратическое отклонение s(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:
|
|
|
19. Законы распределения дискретных случайных величин. Так как дискретная случайная величина имеет конечное или счётное множество значений, то их можно просто перечислить и указать соответствующие вероятности. Это можно сделать, например, в форме таблицы
|
X |
x1 |
x2 |
... |
xn |
... |
|
P |
p1 |
p2 |
|
pn |
|
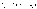 -
вероятностьтого, чтоX примет
значение x
-
вероятностьтого, чтоX примет
значение x . Такую
таблицу называют рядом
распределения.
. Такую
таблицу называют рядом
распределения.События  …
несовместимы и в результате опыта одно
из них обязательно происходит. Из этого
следует
…
несовместимы и в результате опыта одно
из них обязательно происходит. Из этого
следует
2).
Биномиальный закон распределения.
Случайная величина может принимать
значения 0,1,2,…,n и
каждому значению X=m соответствует
вероятность 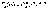 ,
гдеp+q=1.
Этот закон распределения считается
заданным, если известны числа n и p,
через которые выражаются все вероятности.
Случайную величину подчинённою этому
закону можно назвать числом
появлении события в n независимых
опытах.
,
гдеp+q=1.
Этот закон распределения считается
заданным, если известны числа n и p,
через которые выражаются все вероятности.
Случайную величину подчинённою этому
закону можно назвать числом
появлении события в n независимых
опытах.
З).
Пуассоновский закон распределения.
Случайная велbчина
имеет возможные значения 0,1,2,3,…… и
каждому значению Х=m соответствует
вероятность  ,где
,где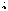 -
некоторый параметр, вероятностный
смысл которого будет указан несколько
страниц спустя.
-
некоторый параметр, вероятностный
смысл которого будет указан несколько
страниц спустя.
4).
Гипергеометрический закон распределения.
Возможные значения X:
0,1,…,n.
И каждому значению X=m соответствует
вероятность P(X=m)=P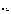 =
=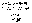 .
. Эта
случайная величина, например, равна
числу m бракованных
изделий среди n взятых
наугад из партии объёма N,содержащей M бракованных
изделий.
Эта
случайная величина, например, равна
числу m бракованных
изделий среди n взятых
наугад из партии объёма N,содержащей M бракованных
изделий.
18. Дискретная случайная величина и закон ее распределения
Реальное
содержание понятия «случайная
величина»
может быть выражено с помощью такого
определения: случайной
величиной,
связанной с данным опытом, называетсявеличина,
которая при каждом осуществлении этого
опыта принимает то или иное числовое
значение, причем заранее неизвестно,
какое именно. Случайные
величиныбудем
обозначать буквами 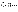 Определение. Говорят,
что задана дискретная
случайная величина
Определение. Говорят,
что задана дискретная
случайная величина 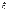 ,
если указано конечное или счетное
множество чисел
,
если указано конечное или счетное
множество чисел
 и
каждому из этих чисел
и
каждому из этих чисел 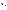 поставлено
в соответствие некоторое положительное
число
поставлено
в соответствие некоторое положительное
число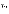 ,
причем
,
причем

Числа 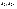 называются
возможнымизначениями
случайной величины
называются
возможнымизначениями
случайной величины  ,
а числа
,
а числа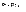 -вероятностями этих
значений (
-вероятностями этих
значений (  ).Таблица
).Таблица
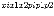 называется законом
распределения дискретной случайной
величины
называется законом
распределения дискретной случайной
величины  .
.
Если
возможными значениями дискретной
случайной величины  являются0,
1, 2, …, n,
а соответствующие им вероятности вычисляются
по формуле
Бернулли:
являются0,
1, 2, …, n,
а соответствующие им вероятности вычисляются
по формуле
Бернулли:

то
говорят, что случайная
величина 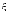 имеетбиномиальный
закон распределения:
имеетбиномиальный
закон распределения:

Пусть
заданы натуральные
числа m, n, s, причем 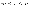 Если
возможными значениямидискретной
случайной величины
Если
возможными значениямидискретной
случайной величины 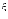 являются0,1,2,…,
m,
а соответствующие им вероятности выражаются
по формуле
являются0,1,2,…,
m,
а соответствующие им вероятности выражаются
по формуле

то
говорят, что случайная
величина 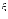 имеетгипергеометрический
закон распределения.
имеетгипергеометрический
закон распределения.
Другими часто встречающимися примерами законов распределения дискретной случайной величины являются:
геометрический
 где
где 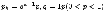 ;
;
Закон распределения Пуассона:
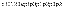
где
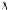 -
положительное постоянное.
-
положительное постоянное.
Закон
распределения Пуассона является
предельным для биномиального при  ,
, ,
,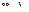 .
Виду этого обстоятельства при большихn и
малых p биномиальные вероятности
вычисляются приближенно по формуле
Пуассона:
.
Виду этого обстоятельства при большихn и
малых p биномиальные вероятности
вычисляются приближенно по формуле
Пуассона:
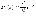 где
где 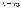 .
.
20. Характеристикой среднего значения случайной величины является математическое ожидание.
Математическим ожиданием M(x) дискретной случайной величины X называется сумма произведений всех ее значений на их вероятности.
M(X)
=
a
= x1p1
+ x2p2
+ … + xnpn
=
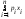
Математическое ожидание обладает следующими свойствами.1. Математическое ожидание постоянной величины равно самой постоянной:M(c) = c.
2. Постоянный множитель можно выносить за знак математического ожидания:M(kX) = kM(X).
3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:M(X ± Y) = M(X) ± M(Y).
4.
Математическое ожидание произведения
независимых случайных величин равно
произведению их математических
ожиданий:M(XY)
= M(X) M(Y).
M(Y).
5. Математическое ожидание отклонения случайной величины от ее математического ожидания (X – M(X)) равно нулю:M(X – M(X)) = 0.
21/ Дисперсией D(X) случайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидани D(X) = M[X – M(X)]2
Дисперсию удобно вычислять по формуле D(X) = M(X2) – [M(X)]2
Дисперсия обладает следующими свойствами.1. Дисперсия постоянной величины равна нулю:D(c) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат:D(kX) = k2D(X).
3. Дисперсия суммы независимых случайных величин равна сумме их дисперсий:D(X ± Y) = D(X) + D(Y).
Наряду
с дисперсией в качестве показателя
рассеяния случайной величины используют
среднее квадратическое отклонение
 ,
определяемое по формуле
,
определяемое по формуле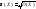
22. Функция распределения случайной величины.
Для описания закона распределения случайной величины X можно рассматривать не вероятность события X=x, а вероятность события X < x, где x – переменная..Функцией распределения случайной величины X называется функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x: F(X) = P(X < x)
Функция распределения обладает следующими свойствами.
1. Значения F(x) принадлежат отрезку [0;1]: 0 ≤ F(x) ≤ 1.
2. Функция F(x) является неубывающей функцией: F(x2) ≥ F(x1), если x2 > x1.
3. Вероятность попадания случайной величины X в интервал [x1,x2) равна приращению F(x) на этом интервале: P(x1 ≤ X < x2) = F(x2) – F(x1).
4. Если все возможные значения случайной величины X принадлежат интервалу (a,b), то F(x) = 0 при x ≤ a и F(x) = 1 при x ≥ b.
Числовые характеристики непрерывной случайной величины.
Математическое ожидание непрерывной случайной величины X определяется равенством
M(X)
=
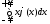
Дисперсия
непрерывной случайной величины X
определяется равенство
D(X)
=
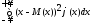
Модой M0(X) случайной величины X называется ее наиболее вероятное значение (для которого вероятность Pi или плотность вероятности φ(x) достигает максимума).
Медианой Me(X) непрерывной случайной величины X называется такое ее значение, для которого
P(X
< Me(X))
= P(X > Me(X))
=
 .
.
Начальным моментом k-ого порядка случайной величины X называется математическое ожидание k-ой степени этой величины:
 .Если
X
– дискретная случайная величина, то
.Если
X
– дискретная случайная величина, то

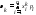 ЕслиX
– непрерывная случайная величина, то
ЕслиX
– непрерывная случайная величина, то
 Центральным
моментомk-ого
порядка случайной величины X
называется величина
Центральным
моментомk-ого
порядка случайной величины X
называется величина
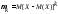 и
и
Для
дискретной величины
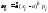
Для непрерывной величины
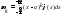
23. Плотность распределения вероятностей непрерывной случайной величины.
Как отмечалось в 3.3, функция распределения непрерывной случайной величины является непрерывной функцией. Кроме того, эта функция дифференцируема, за исключением, быть может, отдельных точек. Тогда для непрерывной случайной величины вероятность любого отдельно взятого значения x0 равна нулю, т.е. P(X = x0) = 0 и
P(x1 < X < x2) = F(x2) – F(x1)
Таким образом, для непрерывной случайной величины вероятность попадания на интервал не зависит от того, является ли этот интервал открытым или закрытым.
Непрерывную случайную величину можно задать с помощью плотности вероятности.
Плотностью
распределения вероятностей
φ(x)
непрерывной случайной величины X
называют первую производную от функции
F(x):
φ(x)
= F (x)
(x)
Плотность φ(x) иногда называют дифференциальным законом распределения, а его график – кривой распределения.Плотность распределения вероятностей обладает следующими свойствами.
1. Это неотрицательная функция: φ(x) ≥ 0.
2. Вероятность попадания случайной величины на интервал (a;b) имеет вид
P(a
< X
< b)
=

3.
Функция распределения непрерывной
случайной величины связана с плотностью
вероятностей, а именно
F(x)
=
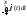 =
1
=
1
4.
Несобственный интеграл от плотности
распределения φ(x)
в пределах от - до
+
до
+ равен
единице:
равен
единице: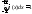
Из свойств плотности вероятностей следует, что ее график лежит не ниже оси абсцисс, а площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.
24. Равномерное распределение. Непрерывная величина Х распределена равномерно на интервале (a, b), если все ее возможные значения находятся на этом интервале и плотность распределения вероятностей постоянна:
 Для
случайной величины Х ,
равномерно распределенной в интервале
(a, b)
(рис. 4), вероятность попадания в любой
интервал (x1, x2),
лежащий внутри интервала (a, b),
равна:
Для
случайной величины Х ,
равномерно распределенной в интервале
(a, b)
(рис. 4), вероятность попадания в любой
интервал (x1, x2),
лежащий внутри интервала (a, b),
равна:
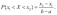
25. Показательное распределение. Непрерывная случайная величина Х имеет показательное распределение, если плотность распределения ее вероятностей выражается формулой:

Время Т безотказной работы компьютерной системы есть случайная величина, имеющая показательное распределение с параметром λ , физический смысл которого – среднее число отказов в единицу времени, не считая простоев системы для ремонта.
26. Нормальное (гауссово) распределение. Случайная величина Х имеет нормальное (гауссово) распределение, если плотность распределения ее вероятностей определяется зависимостью:
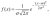 где m = M(X)
,
где m = M(X)
, 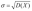 .
.
При  нормальное
распределение называется стандартным.Определение
неизвестных параметров распределения.пусть x1,
x2,
..., xn -
наблюдаемые значения непрерывной
случайной величины
нормальное
распределение называется стандартным.Определение
неизвестных параметров распределения.пусть x1,
x2,
..., xn -
наблюдаемые значения непрерывной
случайной величины 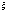 ,
и пусть ее плотность распределения
вероятностей зависит от двух неизвестных
параметровA и B,
т.е. имеет вид
,
и пусть ее плотность распределения
вероятностей зависит от двух неизвестных
параметровA и B,
т.е. имеет вид  .
Один из методов нахождения неизвестных
параметровA и B состоит
в том, что их выбирают таким образом,
чтобы математическое ожидание и
дисперсия теоретического распределения
совпали с выборочными средними
значением
.
Один из методов нахождения неизвестных
параметровA и B состоит
в том, что их выбирают таким образом,
чтобы математическое ожидание и
дисперсия теоретического распределения
совпали с выборочными средними
значением 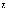 и
дисперсией
и
дисперсией :
:
|
|
|
где
|
|
(67) |
Из
двух полученных уравнений (66)
находят неизвестные параметрыA и B.
Так, например, если случайная
величина 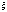 подчиняется
нормальному закону распределения
вероятностей, то ее плотность распределения
вероятностей
подчиняется
нормальному закону распределения
вероятностей, то ее плотность распределения
вероятностей
 зависит
от двух параметров a и
зависит
от двух параметров a и  .
Эти параметры, как мы знаем, являются
соответственно математическим ожиданием
и средним квадратическим отклонением
случайной величины
.
Эти параметры, как мы знаем, являются
соответственно математическим ожиданием
и средним квадратическим отклонением
случайной величины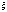 ;
поэтому равенства (66)
запишутся так:
;
поэтому равенства (66)
запишутся так:
|
|
(68) |
Следовательно, плотность распределения вероятностей имеет вид

27. Правило трёх сигм
При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю.Это правило называется правилом трех сигм.
Стандартное отклонение (иногда среднеквадратичное отклонение) — показатель рассеивания значений случайной величиныотносительно еёматематического ожидания. .

где  — стандарт, стандартное отклонение, несмещенная оценка среднеквадратического отклоненияслучайной величины X относительно её математического ожидания;
— стандарт, стандартное отклонение, несмещенная оценка среднеквадратического отклоненияслучайной величины X относительно её математического ожидания; — дисперсия;
— дисперсия; — i-й элементвыборки;
— i-й элементвыборки; — среднее арифметическое выборки;
— среднее арифметическое выборки; — объём выборки.
— объём выборки.
Следует отметить отличие стандарта (в знаменателе n − 1) от корня из дисперсии(среднеквадратическогоотклонения)(в знаменателе n), при малом объёме выборки оценка дисперсии через последнюю величинуявляется несколько смещенной, при бесконечно большом объёме выборки разница между указаннымивеличинами исчезает. Выборка — лишь часть генеральной совокупности. Генеральная совокупность —абсолютно все возможные результаты.
Правило 3-х сигм ( ) — практически все значения нормально распределённой случайной величины лежатв интервале
) — практически все значения нормально распределённой случайной величины лежатв интервале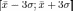 . Более строго не менее чем с 99,7 % достоверностью, значениенормально распределенной случайной величины лежит в указанном интервале. При условии что величина
. Более строго не менее чем с 99,7 % достоверностью, значениенормально распределенной случайной величины лежит в указанном интервале. При условии что величина истинная, а не полученная в результате обработки выборки. Если же истинная величина неизвестна, тоследует пользоваться не σ, аs. Таким образом, правило 3-х сигм преобразуется в правило трех s
истинная, а не полученная в результате обработки выборки. Если же истинная величина неизвестна, тоследует пользоваться не σ, аs. Таким образом, правило 3-х сигм преобразуется в правило трех s
28.
Закон
больших чисел в теории
вероятностейутверждает, что
эмпирическое среднее (среднее
арифметическое) конечной выборки из
фиксированного распределения близко
к теоретическому среднему (математическому
ожиданию) этого распределения. В
зависимости от вида сходимости различают
слабый закон больших чисел, когда имеет
место сходимость по вероятности, и
усиленный закон больших чисел, когда
имеет место сходимость почти
наверняка.Теоретическим обоснованием
этого замечательного свойства случайных
явлений являетсязакон
больших чисел.
Названием "закон больших чисел"
объединена группа теорем, устанавливающих
устойчивость средних результатов
большого количества случайных явлений
и объясняющих причину этой
устойчивости.Простейшая форма закона
больших чисел, и исторически первая
теорема этого раздела - теорема
Бернулли,
утверждающая, что если вероятность
события одинакова во всех испытаниях,
то с увеличением числа испытаний частота
события стремится к вероятности события
и перестает быть случайной.Теорема
Пуассона утверждает,
что частота события в серии независимых
испытаний стремится к среднему
арифметическому его вероятностей и
перестает быть случайной.В основе
качественных и количественных утверждений
закона больших чисел лежит неравенство
Чебышева.
Оно определяет верхнюю границу
вероятности того, что отклонение
значения случайной величины от ее
математического ожидания больше
некоторого заданного числа. Замечательно,
что неравенство Чебышева дает оценку
вероятности события  для
случайной величины, распределение
которой неизвестно, известны лишь ее
математическое ожидание и дисперсия.
для
случайной величины, распределение
которой неизвестно, известны лишь ее
математическое ожидание и дисперсия.
Неравенство
Чебышева. Если случайная величина x имеет
дисперсию, то для любого e > 0
справедливо неравенство 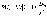 ,
гдеMx и Dx -
математическое ожидание и дисперсия
случайной величины x
,
гдеMx и Dx -
математическое ожидание и дисперсия
случайной величины x
.
29.
Закон
больших чисел (теорема Чебышева)
теорему Чебышева. Эта теорема устанавливает
связь между средним арифметическим
наблюденных значений случайной величины
и ее математическим ожиданием.Имеется
случайная величина 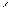 с
математическим ожиданием
с
математическим ожиданием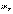 и
дисперсией
и
дисперсией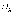 .
Над этой величиной производится
.
Над этой величиной производится независимых
опытов и вычисляется среднее арифметическое
всех наблюденных значений величины
независимых
опытов и вычисляется среднее арифметическое
всех наблюденных значений величины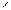 .
Требуется найти числовые характеристики
этого среднего арифметического -
математическое ожидание и дисперсию
- и выяснить, как они изменяются с
увеличением
.
Требуется найти числовые характеристики
этого среднего арифметического -
математическое ожидание и дисперсию
- и выяснить, как они изменяются с
увеличением .
.
Обозначим: -
значение величины
-
значение величины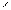 в
первом опыте;
в
первом опыте;
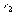 -
значение величины
-
значение величины  во
втором опыте, и т. д.
во
втором опыте, и т. д.
Очевидно,
совокупность величин 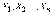 представляет
собой
представляет
собой независимых
случайных величин, каждая из которых
распределена по тому же закону, что и
сама величина
независимых
случайных величин, каждая из которых
распределена по тому же закону, что и
сама величина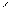 .
Рассмотрим среднее арифметическое
этих величин:
.
Рассмотрим среднее арифметическое
этих величин:
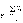 .Случайная
величина
.Случайная
величина 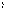 есть
линейная функция независимых случайных
величин
есть
линейная функция независимых случайных
величин .
Найдем математическое ожидание и
дисперсию этой величины. Согласно
правилам
.
Найдем математическое ожидание и
дисперсию этой величины. Согласно
правилам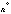 10
для определении числовых характеристик
линейных функций получим:
10
для определении числовых характеристик
линейных функций получим:
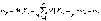 ;
;
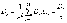 .
.
Теорема Чебышева и устанавливает в точной количественной форме это свойство устойчивости среднего арифметического. Она формулируется следующим образом:
Запишем
теорему Чебышева в виде формулы. Для
этого напомним смысл термина «сходится
по вероятности». Говорят, что случайная
величина  сходится
по вероятности к величине
сходится
по вероятности к величине ,
если при увеличении
,
если при увеличении вероятность
того, что
вероятность
того, что и
и будут
сколь угодно близки, неограниченно
приближается к единице, а это значит,
что при достаточно большом
будут
сколь угодно близки, неограниченно
приближается к единице, а это значит,
что при достаточно большом
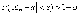 ,
,
где 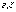 -
произвольно малые положительные числа.
-
произвольно малые положительные числа.
Запишем
в аналогичной форме теорему Чебышева.
Она утверждает, что при увеличении  среднее
арифметическое
среднее
арифметическое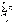 сходится
по вероятности к
сходится
по вероятности к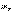 ,
т. е.
,
т. е.
 .
.
Докажем это неравенство.
Доказательство. Выше было показано, что величина
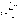 имеет
числовые характеристики
имеет
числовые характеристики
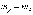 ;
; 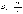 .
.
Применим
к случайной величине  неравенство
Чебышева, полагая
неравенство
Чебышева, полагая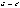 :
: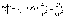 .
.
Как
бы мало ни было число  ,
можно взять
,
можно взять таким
большим, чтобы выполнялось неравенство
таким
большим, чтобы выполнялось неравенство
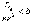 где
где  -
сколь угодно малое число.
-
сколь угодно малое число.
Тогда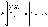 ,откуда,
переходя к противоположному событию,
имеем:
,откуда,
переходя к противоположному событию,
имеем: ,
,
что и требовалось доказать.
30. Закон больших чисел. Теорема бернулли
Закон больших чисел в форме Бернулли состоит в следующем: с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом числе опытов частота появления события А как угодно мало отличается от его вероятности, т. е.
|
|
|
иными
словами, при
неограниченном увеличении числа n
опытов частота m/n события А сходится
по вероятности к
Р(А).
Доказательство:
Рассмотрим
случайную величину 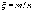 .
Так какM(m)=np и D(m)=npq
то
.
Так какM(m)=np и D(m)=npq
то
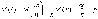
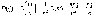
Применим
к случайной величине  вторую
лемму Чебышева:
вторую
лемму Чебышева:

Переходя
к пределу при 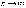 ,
очевидно, имеем
,
очевидно, имеем
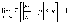
31
. Совместное рассмотрение двух или
нескольких случайных величин приводит
к понятию системы случайных величин.
Условимся систему нескольких случайных
величин  обозначать
обозначать .
Такая система называется такжемногомерной
случайной величиной.
При рассмотрении системы случайных
величин удобно пользоваться геометрической
интерпретацией системы. Например,
систему двух случайных величин
.
Такая система называется такжемногомерной
случайной величиной.
При рассмотрении системы случайных
величин удобно пользоваться геометрической
интерпретацией системы. Например,
систему двух случайных величин 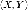 можно
рассматривать как случайную точку на
плоскости
можно
рассматривать как случайную точку на
плоскости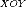 с
координатами
с
координатами и
и или
как случайный вектор на плоскости со
случайными составляющими
или
как случайный вектор на плоскости со
случайными составляющими и
и .
По аналогии систему
.
По аналогии систему случайных
величин можно рассматривать как
случайную точку в
случайных
величин можно рассматривать как
случайную точку в -мерном
пространстве или как n-мерный случайный
вектор.При изучении систем случайных
величин ограничимся подробным
рассмотрением системы двух случайных
величин.Закон
распределения вероятностей системы
случайных величиЗаконом
распределения системы случайных величин
называется соотношение, устанавливающее
связь между областями возможных значений
системы случайных величин и вероятностями
появления системы в этих областях.[/b]Так
же, как и для одной случайной величины,
закон распределения системы случайных
величин может быть задан в различных
формах. Рассмотрим таблицу распределения
вероятностей системы дискретных
случайных величин. Пусть
-мерном
пространстве или как n-мерный случайный
вектор.При изучении систем случайных
величин ограничимся подробным
рассмотрением системы двух случайных
величин.Закон
распределения вероятностей системы
случайных величиЗаконом
распределения системы случайных величин
называется соотношение, устанавливающее
связь между областями возможных значений
системы случайных величин и вероятностями
появления системы в этих областях.[/b]Так
же, как и для одной случайной величины,
закон распределения системы случайных
величин может быть задан в различных
формах. Рассмотрим таблицу распределения
вероятностей системы дискретных
случайных величин. Пусть  и
и —
дискретные случайные величины, возможные
значения которых
—
дискретные случайные величины, возможные
значения которых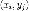 ,
где
,
где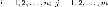 Тогда
распределение системы таких случайных
величин может быть охарактеризовано
указанием вероятностей
Тогда
распределение системы таких случайных
величин может быть охарактеризовано
указанием вероятностей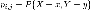 того,
что случайная величина
того,
что случайная величина примет
значение
примет
значение и
одновременно с этим случайная
величина
и
одновременно с этим случайная
величина примет
значение
примет
значение .
Вероятности
.
Вероятности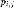 фиксируют
в таблицеТакая таблица называется
таблицей распределения системы двух
дискретных случайных величин с конечным
числом возможных значений. Все возможные
события
фиксируют
в таблицеТакая таблица называется
таблицей распределения системы двух
дискретных случайных величин с конечным
числом возможных значений. Все возможные
события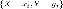 при
при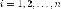
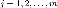 составляют
полную группу несовместных событий,
поэтом
составляют
полную группу несовместных событий,
поэтом


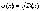 .
.