
Раздел 5. Системы линейных уравнений.
5.1. Матричная запись линейной системы.
Определение. Системой линейных алгебраических уравнений,содержащейmуравнений и пнеизвестных , называется выражение следующего вида:
 (1)
(1)
где
![]() - неизвестные,
- неизвестные,![]() - коэффициент изi-го
уравнения при неизвестном
- коэффициент изi-го
уравнения при неизвестном![]() ,
,![]() ‑
свободный членi-го
уравнения.
‑
свободный членi-го
уравнения.
Введем обозначения:
 - матрица, составленная из коэффициентов
системы;
- матрица, составленная из коэффициентов
системы;
 - столбец неизвестных,
- столбец неизвестных, - столбец свободных членов.
- столбец свободных членов.
Используя введенные обозначения и правила действия над матрицами, систему (1) можно записать в матричной форме
![]() .
(2)
.
(2)
Определение.Совокупность чисел![]() называетсярешением системы(1), если
после подстановки в каждое из уравнений
(1) вместо неизвестных
называетсярешением системы(1), если
после подстановки в каждое из уравнений
(1) вместо неизвестных![]() соответствующих чисел
соответствующих чисел![]()
![]() ,
это уравнение превращается в верное
равенство.
,
это уравнение превращается в верное
равенство.
Определение.Система(1) называетсясовместной,если она имеет хотя бы одно решение, инесовместнойв противном случае.
Мы начнем с исследования частного случая
системы (1), когда
![]() ,
т.е. число уравнений равно числу
неизвестных, и при этом матрицаАсистемы невырожденная.
,
т.е. число уравнений равно числу
неизвестных, и при этом матрицаАсистемы невырожденная.
5.2. Решение линейной системы с помощью обратной матрицы.
Рассмотрим частный случай, когда число уравнений совпадает с числом неизвестных.
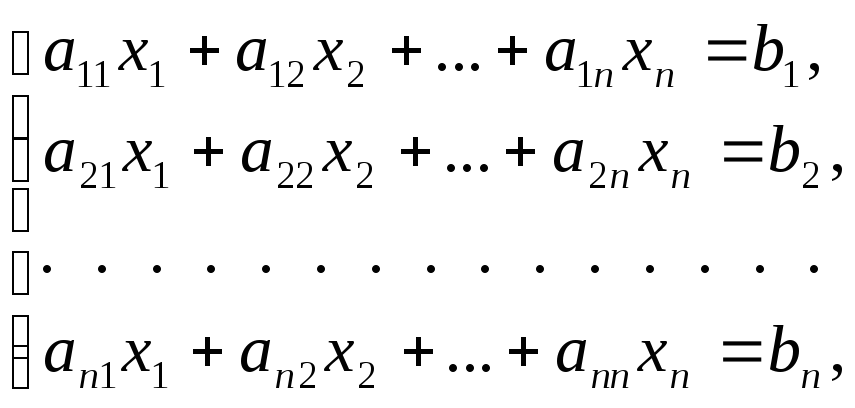 (1)
(1)
или
![]() .
(2)
.
(2)
В этом случае
![]() и матрица системы
и матрица системы
 - квадратная.
- квадратная.
Покажем, что решение системы (1) сводится к решению матричного уравнения (2).
Действительно, связь между системой
(1) и уравнением (2) заключается в том, что
совокупность чисел
![]() является решением данной системы тогда
и только тогда, когда
является решением данной системы тогда
и только тогда, когда

есть решение уравнения (2). Это утверждение означает выполнение равенства

или
 .
.
Последнее равенство, как равенство матриц, равносильно системе равенств

которая означает, что
![]() - решение системы (1).
- решение системы (1).
Итак, решение системы (1) сводится к решению уравнения (2).
Так как
![]() ,
то существует обратная матрица
,
то существует обратная матрица![]() .
Умножим обе части матричного уравнения
(2) на
.
Умножим обе части матричного уравнения
(2) на![]() слева, получим:
слева, получим:![]() .
Отсюда, так как
.
Отсюда, так как![]() ,
находим
,
находим
![]() .
(3)
.
(3)
Следовательно, если уравнение (2) имеет
решение, то оно задается формулой (3). С
другой стороны, подставив
![]() в (2) получим
в (2) получим
![]() ,
,
поэтому (3) является единственным решением уравнения (2).
Пример.Записать в матричной форме и решить систему при помощи обратной матрицы
 .
.
Решение.Запишем систему в матричной
форме:![]() .
Здесь
.
Здесь
 ,
, ,
, .
.
Имеем:
 .
.
Следовательно, существует обратная
матрица
![]() .
Найдем ее:
.
Найдем ее:

Наконец,
 ,
,
откуда
![]() .
.
5.3. Правило Крамера.
Пусть дана система плинейных уравнений спнеизвестными
 (1)
(1)
или
![]() (2)
(2)
с действительными или комплексными коэффициентами.
Введем обозначения:

 ,
,
где - определитель
системы, а![]() получается заменой элементовi–го столбца вна
столбец из свободных членов
получается заменой элементовi–го столбца вна
столбец из свободных членов![]() .
.
Теорема (правило Крамера).Если
определитель линейной системы (1) отличен
от нуля![]() ,
то система имеет и притом единственное
решение, которое определяется по
формулам:
,
то система имеет и притом единственное
решение, которое определяется по
формулам:
![]() .
(3)
.
(3)
Доказательство.
Было доказано, что решение системы (1)
сводится к решению матричного уравнения
(2) и так как
![]() ,
то существует единственное решение
уравнения (2), которое определяется
формулой
,
то существует единственное решение
уравнения (2), которое определяется
формулой
![]() .
(4)
.
(4)
Напомним, что
 ,
,
где
![]() - алгебраическое дополнение элемента
- алгебраическое дополнение элемента![]() матрицыА, тогда
матрицыА, тогда
 .
.
Раскрывая определитель
![]() поi-му столбцу,
получим,
поi-му столбцу,
получим,![]() ,
следовательно,
,
следовательно,

откуда
![]() .
.
Пример.Записать в матричной форме и решить систему при помощи правила Крамера
 .
.
Решение.Запишем систему в матричной
форме:![]() .
Здесь
.
Здесь
 ,
, ,
, .
.
Имеем:
 .
.
Найдем
 ,
, ,
,
Наконец,
![]() ,
,![]() ,
,![]()
откуда
![]() .
.
