
- •Линейная алгебра и аналитическая геометрия
- •1. Множество всех алгебраических многочленов степени, не превышающей натурально го числа n. Легко убедиться, что если х и у - многочлены степени не выше n,то они будут обладать свойствами 1 – 8 ;
- •4. Множество всех функций, непрерывных на отрезке [ a , b ], с поточечными для функций операциями сложения и умножения на число.
- •Формула определения координат вектора для плоских задач
- •Метод элементарных преобразований
- •Метод окаймления миноров
- •Элементарными преобразованиями строк называют:
Линейная алгебра и аналитическая геометрия
Определение матрицы размера m×n.
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Определения квадратной, треугольной, диагональной и единичной матриц.
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпдают: m=n. Число m=n называется порядком квадратной матрицы.
Квадратная матрица А порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е. aij=0, при всех i>j.
Квадратная матрица А порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. aij=0, при всех i<j.
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю.
Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E n, где n - порядок матрицы.
Определение равенства матриц.
Две
матрицы A и B называются
равными, если они имеют одинаковое число
строк и столбцов и их соответствующие
элементы равны aij = bij.
Так
если ![]() и
и ![]() ,
то A=B,
если a11 =
b11,
a12 =
b12,
a21 =
b21 и a22 =
b22.
,
то A=B,
если a11 =
b11,
a12 =
b12,
a21 =
b21 и a22 =
b22.
Операции сложения матриц и умножения матрицы на число.
Сложение: Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,
![]()
![]() или
или
Умножение
матрицы на число:
Для
того чтобы умножить матрицу A на
число k нужно
каждый элемент матрицы A умножить
на это число. Таким образом, произведение
матрицы A на
число k есть
новая матрица, которая определяется
по правилу ![]() или
или ![]() .
.
Для любых чисел a и b и матриц A и B выполняются равенства:


 .
.
Операция умножения матриц.
Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:
![]() .
.
Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c13, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.
В общем случае, если мы умножаем матрицу A = (aij) размера m×n на матрицу B = (bij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.
Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,
 .
.
Операция транспонирования матрицы.
Рассмотрим
произвольную матрицу A из m строк
и n столбцов.
Ей можно сопоставить такую
матрицу B из n строк
и m столбцов,
у которой каждая строка является столбцом
матрицы A с
тем же номером (следовательно, каждый
столбец является строкой матрицы A с
тем же номером). Итак, если ![]() ,
то
,
то ![]() .
.
Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.
Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT.
Связь
между матрицей A и
её транспонированной можно записать в
виде ![]()
Определение перестановки и инверсии в ней.
Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3, . . . , n в строчку одно за другим. Говорят, что в данной перестановке два числа образуют инверсию (беспорядок), если большее из чисел в данной перестановке стоит левее меньшего. В противном случае эти два числа образуют порядок.
Теорема о числе перестановок.
Теорема
7.2 (о
числе перестановок). Число всех
перестановок множества из n элементов
определяется формулой![]() (считаем,
что по определению
(считаем,
что по определению![]()
Пример 3. Цифры 0, 1, 2, 3 записаны на 4-х карточках. Сколько различных 4-значных цифр можно составить из этих карточек?
Решение. Число различных комбинаций из 4-х цифр равно 4!; 3! комбинаций, начинающихся с 0, следует исключить. В результате количество различных 4-значных чисел равно 4! - 3! = 18.
Определение. Упорядоченные наборы, состоящие из k элементов, взятых из данных n элементов, называются размещениями из n элементов по k.
Размещения отличаются друг от друга либо элементами, либо порядком.
Определение транспозиции в перестановке.
Транспозицией называется такое преобразование перестановки, при котором какие – либо два её элемента меняются местами, а все остальные элементы остаются на своих местах.
Четные и нечетные перестановки.
Перестановка называется чётной, если общее количество инверсий есть чётное число и, соответственно, нечётной, если общее количество инверсий, содержащихся в этой перестановке , число нечётное.
Терема об изменении четности перестановки при транспозиции.
Теорема: Все n! перестановок можно записать в таком порядке, что каждая следующая будет получаться из предыдущей с помощью одной транспозиции (такой порядок называется идеальным), при этом ни одна перестановка не встретится дважды, а начинать можно с любой перестановки. Следствие из теоремы: из какой–либо перестановки n-ой степени можно получить любую другую перестановку n-ой степени с помощью нескольких транспозиций. Теорема 2: Любая транспозиция меняет чётность перестановки на противоположную.
Вычисление определителя 2-го порядка.
Определителем
2-го порядка называют число,
представленное в виде специальнойконструкции: ![]() =
=![]() ,
которой ставят
в соответствие число:
,
которой ставят
в соответствие число: ![]() .
Записывают:
.
Записывают:
![]() =
=![]() =
=![]() . (1)
. (1)
Говорят, что правая часть выражения (1) определяет правило еговычисления определителя 2-го порядка.
При использовании определителя применяют термины:
элементы определителя – числа a11, a12, a21, a22;
строки определителя: 1-я строка: пара чисел: a11,a12 , 2-я строка: пара чиселa21,a22;
столбцы определителя: 1-й столбец: пара чисел: a11,a21, 2-й столбец: пара чиселa12,a22;
члены определителя: (a11·a22) и (–a21·a12).
Вычисление определителя 3-го порядка.
Определителем
3-го порядка называют число,
представленное в виде специальнойконструкции: ![]() =
=![]() ,
которой ставят
в соответствие число, определяемое
суммой, составленной из шести слагаемых
(членов определителя):
,
которой ставят
в соответствие число, определяемое
суммой, составленной из шести слагаемых
(членов определителя):
![]() =
=![]() +
+![]() +
+![]() –
–![]() –
–![]() –
–![]() .
.
Определение определителя порядка n.
Определителем или детерминантом n-го порядка называется число записываемое в виде

Определитель
матрицы А есть
число, равное ![]() .
.
Опишем
эту формулу словами. Определителем
квадратной матрицы порядка n на n является
сумма, содержащая n! слагаемых.
Каждое слагаемое представляет собой
произведение nэлементов
матрицы, причем в каждом произведении
содержится элемент из каждой строки и
из каждого столбца матрицы А.
Перед k-ым слагаемым
появляется коэффициент (-1),
если элементы матрицы А в
произведении упорядочены по номеру
строки, а количество инверсий ![]() в k-ой перестановке
множества номеров столбцов нечетно.
в k-ой перестановке
множества номеров столбцов нечетно.
Определитель
матрицы А обычно
обозначается как ![]() ,
также встречается обозначение det(A).
Также можно услышать, что определитель
называют детерминантом.
,
также встречается обозначение det(A).
Также можно услышать, что определитель
называют детерминантом.
Итак, ![]() .
.
Отсюда
видно, что определителем матрицы первого
порядка является элемент этой матрицы ![]() .
.
Как изменится определитель при транспонировании матрицы?
При
транспонировании матрицы определитель
не меняется, то есть ![]() .
.
Чему равен определитель, имеющий строку или столбец, целиком состоящий из нулей?
Если матрица содержит нулевую строку, то ее определитель равен нулю.
Как изменится определитель, если его строку или столбец умножить на число?
Если
строку матрицы умножить на число ![]() ,
то ее определитель умножится на это
число.
,
то ее определитель умножится на это
число.
Как изменится определитель, если в нем переставить две строки или два столбца?
Если в матрице А поменять местами две строки, то ее определитель сменит знак.
Как изменится определитель, если к какой-либо его строке прибавить другую строку, умноженную на некоторое число?
Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится.
Чему равен определитель, имеющий две пропорциональные строки?
Если одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю.
Как связаны между собой определители матриц А и λА?
Они пропорциопальны.
Чему равен определитель произведения квадратных матриц А и В?
Определитель произведения двух квадратных матриц равен произведению определителей сомножителей.
Определение минора порядка k.
Ранг матрицы — Рангом системы строк (столбцов) матрицы строк и столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие
Определение минора
 элемента
элемента .
.
Минором
элемента определителя называется
определитель, полученный из исходного
определителя вычеркиванием той строки
и того столбца, которым принадлежит
данный элемент. Обозначают минор
элемента ![]() через
через ![]() .
.
Определение алгебраического дополнения
 элемента
элемента .
.
Алгебраическим
дополнением к
элементу ![]() матрицы
матрицы ![]() называется
число, равное
называется
число, равное ![]() ,
где
,
где ![]() -
определитель матрицы, полученной из
матрицы вычеркиванием i-ой строки и
j-ого столбца. Алгебраическое дополнение
к элементу
-
определитель матрицы, полученной из
матрицы вычеркиванием i-ой строки и
j-ого столбца. Алгебраическое дополнение
к элементу ![]() матрицы
матрицы ![]() обозначается
обозначается ![]() .
.
Теорема Лапласа о вычислении определителя порядка n.
Пусть выбраны любые n строк матрицы A. Тогда определитель матрицы A равен сумме всевозможных произведений миноров n-го порядка, расположенных в этих строках, на их алгебраические дополнения.
![]()
где
суммирование ведётся по всевозможным
номерам столбцов ![]()
Теорема о сумме произведений элементов одной строки на алгебраические дополнения элементов другой строки.
Определитель
матрицы равен сумме произведений
элементов некоторого ряда (строки или
столбца) определителя на их алгебраические
дополнения. Иначе говоря, справедливы
следующие формулы
разложения определителя по j-й
строке (или по
элементам j-й
строки):![]()
и разложения
определителя по k-му
столбцу:![]()
для
любых ![]() .
.
Определение обратной матрицы.
Матрица B называется обратной матрицей для квадратной матрицы A, если AB=BA=E.
Из определения следует, что обратная матрица B будет квадратной матрицей того же порядка, что и матрица A(иначе одно из произведений AB или BA было бы не определено).
Обратная
матрица для матрицы A обозначается ![]() .
Таким образом, если
.
Таким образом, если ![]() существует,
то
существует,
то ![]() .
.
Из
определения обратной матрицы следует,
что матрица A является
обратной для матрицы ![]() ,
то есть
,
то есть ![]() .
Про матрицы A и
.
Про матрицы A и ![]() можно
говорить, что они обратны друг другу
или взаимно обратны.
можно
говорить, что они обратны друг другу
или взаимно обратны.
Условие существования обратной матрицы.
Если
определитель матрицы равен нулю, то
обратная к ней не существует.
Квадратную
матрицу A назовем вырожденной или особенной
матрицей,
если ![]() ,
и невырожденной или неособенной
матрицей,
если
,
и невырожденной или неособенной
матрицей,
если ![]() .
.
Если
квадратная матрица A является
невырожденной, то обратная для нее
существует и ![]() (1)
где
(1)
где ![]() -
алгебраические дополнения к элементам
-
алгебраические дополнения к элементам ![]() .
.
Обратная матрица для квадратной матрицы A существует тогда и только тогда, когда матрица A - невырожденная, обратная матрица единственна, и справедлива формула (1).
Правило вычисления обратной матрицы.
Найти
обратную матрицу для матрицы ![]()
Алгоритм точно такой же, как и для случая «два на два».
Обратную
матрицу найдем по формуле: ![]() ,
где
,
где ![]() –
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы ![]() .
.
1) Находим определитель матрицы.
 Здесь
определитель раскрыт по
первой строке.
Здесь
определитель раскрыт по
первой строке.
Также
не забываем, что ![]() ,
а значит, всё нормально – обратная
матрица существует.
,
а значит, всё нормально – обратная
матрица существует.
2)
Находим матрицу миноров ![]() .
.
Матрица
миноров имеет размерность «три на
три» ![]() ,
и нам нужно найти девять чисел.
,
и нам нужно найти девять чисел.
Я подробно рассмотрю парочку миноров:
Рассмотрим
следующий элемент матрицы:
![]() МЫСЛЕННО
вычеркиваем строку и столбец, в котором
находится данный элемент:
МЫСЛЕННО
вычеркиваем строку и столбец, в котором
находится данный элемент:![]()
Оставшиеся
четыре числа записываем в определитель
«два на два»
![]() Этот
определитель «два на два» и является
минором данного элемента.
Его нужно вычислить:
Этот
определитель «два на два» и является
минором данного элемента.
Его нужно вычислить:
![]() Всё,
минор найден, записываем его в нашу
матрицу миноров:
Всё,
минор найден, записываем его в нашу
матрицу миноров:
Как вы, наверное, догадались, необходимо вычислить девять определителей «два на два». Процесс, конечно, муторный, но случай не самый тяжелый, бывает хуже.
Ну и
для закрепления – нахождение еще одного
минора в картинках:
![]() Остальные
миноры попробуйте вычислить самостоятельно.
Остальные
миноры попробуйте вычислить самостоятельно.
Окончательный
результат:
![]() –
матрица миноров соответствующих
элементов матрицы
–
матрица миноров соответствующих
элементов матрицы ![]() .
.
То, что все миноры получились отрицательными – чистая случайность.
3)
Находим матрицу алгебраических
дополнений ![]() .
.
В
матрице миноров необходимо СМЕНИТЬ
ЗНАКИ строго
у следующих элементов:
![]() В
данном случае:
В
данном случае:![]() –
матрица алгебраических дополнений
соответствующих элементов матрицы B.
–
матрица алгебраических дополнений
соответствующих элементов матрицы B.
4)
Находим транспонированную матрицу
алгебраических дополнений ![]() .
.
![]() –транспонированная
матрица алгебраических дополнений
соответствующих элементов матрицы B.
–транспонированная
матрица алгебраических дополнений
соответствующих элементов матрицы B.
5) Ответ:
![]()
Решение матричного уравнения А·Х = В, если det А ≠ 0?
Рассмотрим матричное уравнение вида А·Х = В, где А – невырожденная квадратная матрица порядка m, В – матрица размера m*р, А и В – известные матрицы. Чтобы найти неизвестную матрицу Х размера m*р умножим обе части матричного уравнения слева на матрицу А-1 – обратную к матрице А: А-1 ·А·Х = А-1·В. Учитывая, что А-1·А = Е, где Е –единичная матрица порядка m, получим решение матричного уравнения:
Х = А-1·В.
Решение матричного уравнения Y·А = В, если det А ≠ 0?
При решении матричного уравнения вида Х·А = В, в котором А – известная невырожденная квадратная матрица порядка m, В –известная матрица размера р* m, умножают обе части матричного уравнения справа на матрицу А-1 – обратную к матрице А: Х·А· А-1 = В· А-1, после чего получают решение:
Х = В·А-1.
Определение арифметического вектора.
Арифметическим
вектором называется упорядоченная
совокупность n чисел. Обозначается ![]() ,
числа
,
числа ![]() называются
компонентами арифметического вектора.
называются
компонентами арифметического вектора.
Для
арифметических векторов определены
линейные операции — сложение арифметических
векторов и умножение вектора на число: ![]() ,
,
для
любых ![]() и
и ![]() и
любого числа
и
любого числа ![]()
Операции над арифметическими векторами.
Для
любых ![]() ,
, ![]() ,
, ![]() из Rn и
любых чисел a, b справедливо:
из Rn и
любых чисел a, b справедливо:
 ,
сложение коммутативно;
,
сложение коммутативно; ,сложение
ассоциативно;
,сложение
ассоциативно;

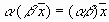 ,
умножение на число ассоциативно;
,
умножение на число ассоциативно; ;
; ,
умножение на число дистрибутивно
относительно сложения элементов;
,
умножение на число дистрибутивно
относительно сложения элементов; ,
умножение вектора на число дистрибутивно
относительно сложения чисел.
,
умножение вектора на число дистрибутивно
относительно сложения чисел.
Определение ортогональных векторов.
Вектора a и b называются ортогональными, если угол между ними равен 90°. Два вектора a и b ортогональны (перпендикулярны), если их скалярное произведение равно нулю. a · b = 0
Определение линейной комбинации векторов.
Линейной комбинацией векторов a1, ..., an с коэффициентами x1, ..., xn называется вектор: x1a1 + ... + xnan.
Определение линейно зависимой и линейно независимой систем векторов.
Вектора a1, ..., an называются линейно независимыми, если не существует нетривиальной комбинации этих векторов равной нулевому вектору. Tоесть вектора a1, ..., an линейно независимы если x1a1 + ... + xnan = 0 тогда и только тогда, когда x1 = 0, ..., xn = 0.
Вектора a1, ..., an называются линейно зависимыми, если существует нетривиальной комбинации этих векторов равная нулевому вектору.
Теорема о необходимом и достаточном условии линейной зависимости системы векторов.
Теорема: Для того чтобы система векторов линейного пространства была линейно зависимой необходимо и достаточно, чтобы какой-нибудь вектор этой системы был линейной комбинацией всех остальных. Доказательство:Дана линейно зависимая система. Нужно доказать, что один вектор линейной комбинации всех остальных.
а1, а2, а3, … аn – ЛЗ система векторов, т.е. среди α1, α2 ,α3 … αn существует число отличное от нуля так, что ЛК α1а1+ α2 а2+α3 а3+…+ αn аn= 0.
Положим для определения, что коэффициент α1 ≠ 0. Разделим обе части последнего равенства на α1 ≠ 0:
Отсюда следует, что а1 - ЛК остальных векторов.
Необходимость доказана.
Достаточность ( ).
Пусть один вектор – это линейная комбинация остальных. Нужно доказать, что система векторов ЛЗ.
Пусть αn = α1 а1+ α2 а2+α3 а3+…+ αn-1 аn-1.
α1 а1+ α2 а2+α3 а3+…+ αn-1 аn-1- 1αn = 0.
Так как есть не нулевой коэффициент, то система векторов а1, а2, а3, … аn- линейно зависима.
Ч.т.д.
Теорема о линейно зависимой подсистеме векторов.
Теорема: Система, содержащая линейно зависимую подсистему, тоже будет линейно зависима.
Док-во: Рассмотрим систему векторов а1, а2, …,ак, ак+1 … аn, где а1, а2,…, ак - линейно зависимый кусочек. α1 а1+ α2а2+ … +αкак= 0. Есть коэффициент отличный от нуля.
Очевидно, что с этими же коэффициентами будет выполняться равенство
α1 а1+ α2 а2+…+αк ак+…+0· ак+1+…+ 0·αn = 0.
Отсюда следует, что система векторов ЛЗ.
Теорема о подсистеме линейно зависимой системы векторов.
Система векторов A1, A2,...,An называется линейно зависимой, если существует ненулевой набор чисел λ1,λ2,...,λn, при котором линейная комбинация векторов λ1*A1+λ2*A2+...+λn*An равна нулевому вектору, то есть система уравнений: A1x1+A2x2+...+Anxn =Θ имеет ненулевое решение. Набор чисел λ1, λ2,...,λn является ненулевым, если хотя бы одно из чисел λ1, λ2,...,λn отлично от нуля.
Определение линейного пространства.
Непустое множество Е элементов любой природы Е = { x, y, z, t, … } называется линейным или векторным пространством над полем действительных чисел R , если выполняются следующие условия:
а) имеется правило, посредством которого любым двум элементам х, у множества Е ставится в соответствие элемент z этого же множества Е, называемый суммой этих элементов : z = x + y;
b) имеется правило, посредством которого каждому элементу х множества Е и любому действительному числу λ ставится в соответствие элемент u = λ x , называемый произведением х на λ .
При этом указанные правила ( операции ) удовлетворяют восьми аксиомам:
1) x + y = y + x - коммутативное ( переместительное ) свойство суммы ;
2) ( x + y ) + z = x + (y + z ) - ассоциативное ( сочетательное ) свойство суммы;
3) Существует нулевой элемент 0 Є Е такой, что х + 0 = х для любого элемента х Є Е ;
4) Для любого элемента х Є Е существует противоположный элемент (- х ) Є Е такой, что х + ( - х ) = 0 ;
5) Для любых действительных чисел α и β верно равенство α(βх) = (αβ)х - ассоциативное относительно числового множителя свойство ;
6) 1∙х = х для любого элемента х Є Е ( особая роль числового множителя 1 );
7) Для любого действительного λ и произвольных элементов х, у Є Е выполняется равенство λ ( х + у ) = λ х +λ у - дистрибутивное (распределительное) относительно суммы элементов свойство;
8) Для любых действительных чисел α и β и произвольного элемента хЄ Е верно равенство (α + β ) х = α х + β х - дистрибутивное (распределительное) относительно суммы числовых множителей свойство.
Примеры линейных пространств.
Примеры линейных пространств
