Lesn4_Rjady

Глава V. Ряды Фурье

записи ряда:

An - амплитуда;

n - угловая частота;n - начальная фаза;

A0 - постоянная составляющая функции; I1(x) - главная гармоника;

In (x), n 1- верхние гармоники.

В теории звуковых колебаний главная гармоника называ-

ется основным тоном, а верхние гармоники - обертонами.

Заметим также, что постоянная составляющая A0 является средним значением функции f(x) на отрезке [ l, l]:

l

A0 21l f (x)dx .

l

Разложение (4) называется гармоническим анализом функции. Это разложение характеризуется тремя последовательностями коэффициентов. Данные последовательности называются

спектрами разложения функции:

{An} - амплитудный спектр; { n} - частотный спектр; { n} - фазовый спектр.

Так как получение разложения (4) равносильно нахождению этих трех спектров, то разложение (4) называется также

спектральным анализом функции.

Заметим, что все три спектра дискретны.

Геометрическое представление спектров. Если по оси x отметить частоты, а по оси y - амплитуды (начальные фазы), то получим так называемую спектральную диаграмму амплитуд (начальных фаз).

Перейдем к другой форме записи ряда Фурье.

100

§4. Различные формы записи ряда Фурье.

2.

Ряд Фурье в комплексной форме

Рассмотрим снова разложение (1) функции f(x):

a0

f (x)

an cos(n

x) bn sin(n

x)

2

n 1

l

l

спомним

определения тригонометрических функций

комплексной переменной:

cos z

1

eiz e iz ;

sin z

i

eiz

e iz .

2

2

Положив в них z n x x ,

n Z , запишем гармонику

l

n

In (x) в комплексной форме:

In (x)

= an cos(n

x)

bn sin(n

x)

1

an e

i n x

e

i n x

l

l

2

1

i n x

i n x

1

i n x

1

i n x

2 bni e

=

an bni e

e

2 an bni e

2

.

Введем обозначения:

1

a c ;

1

a

b i

c ;

1

a

b i c

.

(5)

2

0

0

2

n

n

n

2

n

n

n

Преобразуем гармонику, учитывая, что

n

:

n

l

n

In (x) = сnei n x с ne i n x = сnei n x с nei n x .

Тогда разложение функции можно представить так:

	f (x) c0	сnei n x с nei n x .
		n 1
	Его можно записать		еще короче, если	учесть, что
с	с ei 0 x :
0	0
		f (x)	сnei n x .	(6)
			n

Выражение, стоящее в правой части равенства (6), называ-

ется рядом Фурье в комплексной форме.

101

Глава V. Ряды Фурье

апишем коэффициенты Фурье cn и c n в интегральной форме. Согласно равенству (5) и определению коэффициентов Фурье получаем:

cn 12 an

l

= 21l

l

bni			l
	1	1	f (x)
2		l	l

f (x)(cos n x i sin

				l
	cos n xdx		i	f (x)sin n xdx			=
			l
				l
		1		l	i n x
	n x)dx	2l	f (x)e			dx .
			l

Аналогично получаем представление коэффициентов c n:

l

c n 21l f (x)ei n xdx .

l

Учитывая, что

l

l

f ( x)ei 0 x dx ,

c

1

a

1

f (x)dx

1

0

2

0

2l

2l

l

l

можем все коэффициенты записать единообразно:

l

cn 21l f (x)e i n xdx, n Z . (7)

l

Равенство (7) дает представление коэффициентов Фурье в комплексной форме.

комплексной форме ряд Фурье полностью определяется коэффициентами cn. В частности, определяются его спектры. Из равенств (2), (3) и (5) следует:

A a2		b2	| a	n	b i | | 2c	n	| | 2c | 2 | c | .
n	n	n			n		n	n
	n	arg(an bni) arg c n					argcn .

Итак, имеем два спектра ряда Фурье в комплексной форме:

{| cn |} - амплитудный спектр; { arg cn} - фазовый спектр.

Заметим, что мы перешли от вещественной формы ряда Фурье (1) к комплексной форме (6). Возможен и обратный переход.

102

§4. Различные формы записи ряда Фурье.

Обратимся к исследованию свойств спектров ряда Фурье в комплексной форме.

3. Свойства спектров ряда Фурье в комплексной форме

1. Свойство сопряженности. Согласно равенству (5)

				c n cn .	(8)
В частности,	c		a0	- вещественное число.
	0	2

2. Из равенств | c n | | cn | | cn | следует, что амплитудный спектр является четным относительно n.

3. Равенство argc n argcn означает, что фазовый спектр является нечетным относительно n.

4. Как уже было отмечено,

An 2 | cn | .

Следовательно, амплитудный спектр ряда Фурье в комплексной форме в 2 раза меньше, чем в вещественной форме.

5. Если функция f(x) четная, то bn 0 и из равенств (5)

следует, что c n 12 an cn . Это означает, что четная функция

имеет четный вещественный спектр.

Для нечетной функции an 0 , поэтому c n 12 bni cn .

Следовательно, нечетная функция имеет нечетный чисто мнимый спектр.

Мы рассмотрели основные свойства рядов Фурье по тригонометрической системе функций. Вернемся к исследованию рядов Фурье по произвольной ортогональной системе функций.

103

Глава V. Ряды Фурье

Лекция 13

§5. Свойства ряда Фурье по ортогональной системе функций

1. Сходимость функционального ряда в среднем

Как уже отмечалось, ряд Фурье функции f(x) не всегда сходится к этой функции. Тем не менее, на практике часто используется приближенное представление функции f(x) суммой S(x) ее ряда Фурье. Рассмотрим характер такого приближенного представления.

ерой погрешности приближенного равенства f(x) g(x) функций f(x) и g(x), определенных на отрезке [a, b], может

служить не локальная, а интегральная оценка. Как ее можно за-
дать?				y
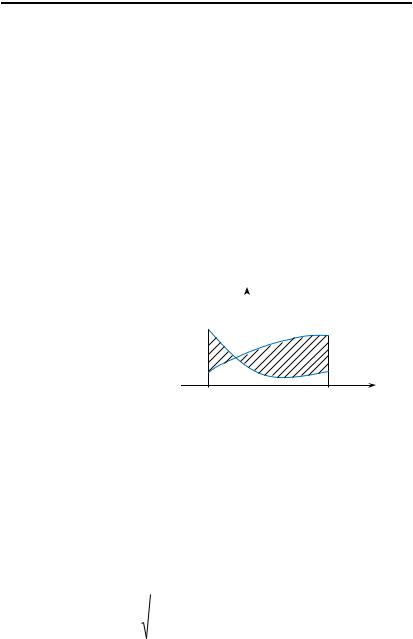
Погрешность можно
оценить площадью		обла-					y = f(x)
сти, заключенной		между
графиками функций f(x)							y = g(x)
и g(x) на	отрезке [a, b]
(см. рис.).	Назовем эту		a	0		b	x
область	криволинейной
полосой.
Более точно,		погрешность		характеризуется			средним от-
						b
клонением функции g(x) от f(x), равным					1	| f (x) g(x) | dx .
					b a
						a

Однако, оно неудобно в работе.

Чтобы аналитически оценить меру допускаемой погрешности, введем следующее понятие.

	Определение 1. Число				= (f, g), определяемое равенством
				1		b
						[ f (x) g(x)]2 dx ,		(1)
				b a
						a

104

§5. Свойства ряда Фурье по ортогональной системе функций.

называется среднеквадратическим отклонением функ-

ции g(x) от функции f(x) на отрезке [a, b].

озьмем теперь функцию g(x) = Sn(x) - частичную сумму ряда Фурье функции f(x). Как ведет себя величина (f, Sn) при n ? Очевидно, если ряд Фурье сходится равномерно к функции f(x), то (f, Sn) 0 при n . А наоборот, что происходит,

если (f, Sn) 0 при n ?

Геометрически условие (f, Sn) 0 означает, что, увеличивая n, можно площадь криволинейной полосы сделать как угодно малой. Поэтому почти во всех точках x отрезка [a, b] последовательность {Sn(x)} сходится к значению функции f(x) и

имеет место равенство	S(x) = f(x). Точек, в которых данное ра-
венство нарушается, может быть конечное или счетное число.
Во многих случаях такой своеобразной сходимости доста-
точно для решения прикладных задач.
Выразим через норму:
		1			|| f (x) g(x) || .	(2)
			b a
Тогда условие	(f,	Sn)			0 равносильно	условию

|| f(x) Sn(x) || 0. Последнее условие и лежит в основе определения следующего понятия.

Определение 2. Функциональный ряд называется сходящимся в среднем (или по норме) к функции f(x) на отрезке [a, b], если его частичные суммы Sn(x) удовлетворяют условию

0 n0 N n N | n n0 || f (x) Sn (x) || . (3)

Сходимость функционального ряда в среднем связана с поточечной и равномерной сходимостями следующим образом.

На конечном отрезке из равномерной сходимости функционального ряда следует сходимость в среднем.

Из сходимости функционального ряда в среднем не следует его поточечная сходимость, и наоборот.

Рассмотрим еще одно свойство ряда Фурье.

105

Глава V. Ряды Фурье

2. Минимальное свойство коэффициентов ряда Фурье

Рассмотрим произвольные функциональные ряды

an n (x) (4)

n 0

по ортогональной системе функций { n(x)}.

В отношении сходимости таких рядов в среднем к заданной функции f(x) особая роль принадлежит ряду Фурье

cn n ( x) . Коэффициенты ряда определяются равенствами

n 0

c	( f , n )			.	(5)
n	||	n	||2

Теорема 1. (Минимальное свойство коэффициентов ряда Фурье). Пусть f(x) L[a, b] и n фиксировано. Среди n-ых частичных сумм всех функциональных рядов вида (4) частичная сумма ряда Фурье функции f(x) дает наименьшее среднеквадратическое отклонение min от этой функции. При этом выполняется равенство

		1			n
2				2		2		2
min		b a	|| f ||		ck		|| k ||	.		(6)
					k 0
Доказательство. Cогласно равенству (5) для коэффициентов
ряда Фурье выполняется равенство ( f ,						n	) c	||	n	||2 .
							n
					n
Возьмем частичную сумму				Sn ak k (x)						произвольно-
					k 0

го функционального ряда вида (4) и вычислим (f, Sn). Согласно равенству (2) (f, Sn) принимает минимальное значение тогда и только тогда, когда минимальное значение принимает квадрат нормы || Sn (x) f (x) ||2 . Имеем:

	n	n
|| Sn f ||2 (Sn f , Sn f )	ak k f ,	ak k f		=
k 0		k 0

106

§5. Свойства ряда Фурье по ортогональной системе функций.

		n	n
		= 0 + ak2 ( k , k ) 2 ak ( f , k ) ( f , f ) =
		k 0	k 0
	n	n	n			n
=	ak2	|| k ||2 2 ak ck || k ||2	ck2	|| k	||2	ck2 || k ||2 || f ||2 =
k 0		k 0	k 0			k 0
		n			n
		= (ak ck )2 || k ||2 ||		f ||2 ck2 || k ||2 .
		k 0			k 0

В последнем выражении от коэффициентов ak зависит только первое слагаемое. Оно неотрицательно и принимает ми-

нимальное значение (равное 0) при

ak сk . Отсюда согласно

равенству (2) получаем

n

min2

1

|| Sn f ||2

1

|| f ||2

ck2

|| k ||2

.

►

b a

b a

k 0

Доказанная теорема означает, что среди всех рядов по ортогональной системе функций, сходящихся к данной функции f(x) в среднем, ее ряд Фурье дает наилучшую сходимость.

Следствие 1. Для ряда Фурье любой функции f(x) L[a, b]

справедливо неравенство Бесселя3:

		|| f ||2 ck2 || k ||2 .			(7)
		k 0
	Доказательство. В равенстве (6) величины 2		и	1	неотри-
				b a
		min
	цательны. Поэтому	при любом натуральном		n	имеем
	n
	|| f ||2 ck2 || k ||2 .	Переходя в этом неравенстве к пределу
	k 0
	при n , получаем неравенство (7).				►

Следствие 2. Коэффициенты тригонометрического ряда Фурье являются бесконечно малыми при n .

3 Бессель Ф.В. (1784 – 1846) – немецкий астроном.

107

Глава V. Ряды Фурье

Доказательство. Функции основной тригонометрической си-

стемы на отрезке [ l, l] удовлетворяют условию:	||	1	||2	l	,
	2		2

|| n ||2 l . Поэтому для тригонометрического ряда Фурье неравенство (7) принимает вид

	2
|| f ||2	l	a0
	2

an2

n 1

bn2		.
n	1

Отсюда следует, что положительные ряды an2 и	bn2 схо-
n 1	n 1

дятся. По необходимому признаку сходимости ряда получаем

lim a		lim	b 0 .	►
n	n	n	n
			3. Замкнутые и полные
			ортогональные системы функций

Определение 3. Ортогональная система функций { n(x)} называется замкнутой в пространстве L[a, b], если для любой функции f(x) этого пространства ее ряд Фурье по данной системе сходится в среднем к f(x) на отрезке [a, b].

Замкнутая ортогональная система функций является своеобразным базисом линейного пространства L[a, b].

Существуют ли такие системы функций?
Теорема 2. Ортогональная система функций { n(x)}		является
	замкнутой в пространстве L[a, b] тогда и только тогда,
	когда для ряда Фурье любой функции f(x)	этого про-
	странства выполняется равенство
	|| f ||2 cn2 || n ||2 .	(8)
	n 0

Равенство (8) называется равенством Парсеваля-Стеклова.

Доказательство. Согласно теореме 1 для частичной суммы

108

§5. Свойства ряда Фурье по ортогональной системе функций.

n
Sn ck k (x)	ряда	Фурье	произвольной	функции
k 0

f (x) L[a;b] выполняется равенство (6). Перейдем в нем к пределу при n :

		1			ck2
lim min2	(Sn , f )			|| f ||2		|| k ||2		0 .
n		b a			k 0
Отсюда следует равенство (8).								►

Теорема 3. (Ляпунова4).

Основная тригонометрическая система функций замкнута в пространстве L[ l, l] кусочно-непрерывных на отрезке [ l, l] функций.

Доказательство опустим.

Определение 4. Ортогональная система функций { n(x)} называется полной в пространстве L[a, b], если в L[a, b] нет функции, ортогональной ко всем функциям n(x) системы и не равной тождественно 0 на отрезке [a, b].

Замечание. Функцию, принимающую нулевое значение во всех точках отрезка [ l, l], кроме конечного числа точек, будем отождествлять с тождественно нулевой функцией.

Теорема 4. Если ортогональная система функций замкнута в пространстве L[a, b], то она полна в этом пространстве.

Доказательство опустим.

Следствие. Основная тригонометрическая система функций является полной в пространстве L[ l, l].

Таким образом, основная тригонометрическая система функций является базисом в пространстве L[ l, l].

4 Ляпунов А.М. (1857 – 1918), русский математик и механик.

109