Inzhenernaya_grafika_Lektsii_Shibaeva

31
На рис. 8.4 показано построение		s′
точки A на грани SDF при помощи пря-
мой, проведенной через вершину пира-
миды. Если дана фронтальная проекция
a' точки A и надо найти горизонтальную
проекцию a, то сначала надо построить			a′
отрезок s' b'. Далее следует найти точку				b′
b по точке b', получить отрезок sb и на	x	d′			f′	e′	o
нем – искомую проекцию
8.2. Пересечение многогранников		d
плоскостью и прямой				b
						e
				a
Линией пересечения многогранни-
ка плоскостью в общем случае является		s
плоский многоугольник, который назы-					f
вают сечением. Такой многоугольник	Рис. 8.4– Построение проекций
можно построить по точкам пересече-	точки на грани пирамиды
ния с плоскостью ребер многогранника

(способ ребер ) или по линям пересечения граней многогранника с плоскостью (способ граней ). Таким образом, задача сводится к определению точек пересечения прямой с плоскостью или к определению линий пересечения плоскостей.

8.2.1. Пересечение многогранника проецирующей плоскостью.

Если секущая плоскость перпендикулярна к одной из плоскостей проекций (т.е. является проецирующей), то проекции фигуры сечения получаются без каких - либо дополнительных построений.

На рис. 8.5 пирамиду SABC пересекает фронтально-проецирующая плоскость , значит, фронтальная проекция сечения располагается на следеv . В данном случае для построения проекций сечения уместно строить точки пересечения ребер пирамиды с плоскостью , это точки D, E, F. Фигура сечения - треугольник, его фронтальная проекция - отрезок прямой d' f '. Горизонтальная проекция сечения построена, исходя из принадлежности точек сечения ребрам пирамиды и соединена с учетом видимости.

Таким образом, если секущая плоскость перпендикулярна одной из плоскостей проекций, то на эту плоскость фигура сечения проецируется в прямую линию, а другие проекции точек фигуры сечения определяются по их принадлежности ребрам или граням.

32

s′

	αv	d′
		e′
x a′	b′	c′	f′	αx o
	b	c	f
				αн
		e
				s

a

d

Рис. 8.5–Пересечение пирамиды проецирующей плоскостью

8.2.2. Пересечение многогранника с прямой линией.

При пересечении поверхности призмы или пирамиды прямой линией получаются две точки. Для них встречается название точек входа и выхода. Прием решения этой задачи происходит по следующей схеме:

1)через данную прямую надо провести вспомогательную плоскость, обычно проецирующую,

2)построить фигуру сечения многогранника этой вспомогательной плос-

костью,

3)определить точки пересечения сторон многоугольника сечения с прямой, эти точки являются точками входа и выхода,

4)определить видимость прямой.

На рис. 8.6 показано построение точек пересечения прямой линии EF с поверхностью пирамиды SABC. Через прямую EF проведена вспомогательная фронтально-проецирующая плоскость . Фронтальная проекция фигуры сечения пирамиды плоскостью сливается с фронтальной проекцией плоскости - следом v. Горизонтальная проекция фигуры сечения (1 2 3) определяется по принадлежности горизонтальных проекций точек 1, 2, 3 горизонтальным проекциям ребер sa, sb, sc соответственно. Точки пересечения горизонтальной проекции прямой EF - ef с горизонтальной проекцией фигуры сечения являются горизонтальными проекциями точек пересечения (m и n) прямой с многогранником. По найденным точкам m, n построены фронтальные проекции (m' и n') точек пересечения. m' и n'.

33

s′

f′

n′

αv e′		1	′
			m′			′
			n′	3	′	m
			2′		f′
						e′
x	a′		b′		c′	o
					c
				3		f

n

e			n
a	m	s	f	e	m

1	2

b	Рис. 8.7– Пересечение
Рис. 8.6– Пересечение пира-
миды с прямой линией	призмы с прямой пинией

Могут быть случаи, когда нет надобности в таких построениях. Пример дан на рис.8.7; положение проекций m и n очевидно, так как боковые грани призмы являются горизонтально - проецирующими плоскостями. По точкам m и n найдены точки m' , n'.

8.3. Взаимное пересечение многогранников

Линиями пересечения многогранников в общем случае являются пространственные замкнутые ломаные линии - многоугольники.

Если один многогранник частично пересекается с поверхностью другого многогранника, то имеем одну замкнутую ломаную линию их взаимного пересечения. Такое пересечение называют неполным проницанием.

Если один многогранник полностью пересекается вторым многогранником, получаем две линии их пересечения - линию входа одного многогранника в другой и линию выхода. Такое взаимное пересечение называют полным проницанием.

Построение линии пересечения многогранников можно производить двумя способами, комбинируя их между собой или выбирая из них тот, который дает более простые построения для конкретного случая пересечения.

Эти способы следующие:

34

1)определяются точки, в которых ребра одного многогранника пересекают грани другого и ребра второго пересекают грани первого многогранника (задача на определение точки пересечения прямой с плоскостью). Через эти точки в определенной последовательности проводят ломаную линию - это и есть линия пересечения многогранников. При этом можно соединять прямыми проекции лишь тех точек , которые принадлежат одной и той же грани первого многогранника, а также и одной грани второго многогранника. Видимыми являются только те из проекций отрезков ломаной линии, которые принадлежат проекциям видимых граней многогранников, все другие проекции отрезков представляются невидимыми;

2)определяют отрезки прямых, по которым грани одного из многогранников пересекают грани другого (это задача на построение линии пересечения двух плоскостей). Эти отрезки и составляют линию пересечения многогранников.

Проекции линии пересечения двух многогранников располагаются внутри контура наложения одноименных проекций многогранников. Если проекция какого - либо ребра одного из многогранников не пересекает общий контур - контур проекций, то ребро не пересекает другой многогранник. Однако, если проекция ребра одного из многогранников пересекает даже и две проекции контура наложения, это еще не означает, что это ребро пересекает второй многогранник.

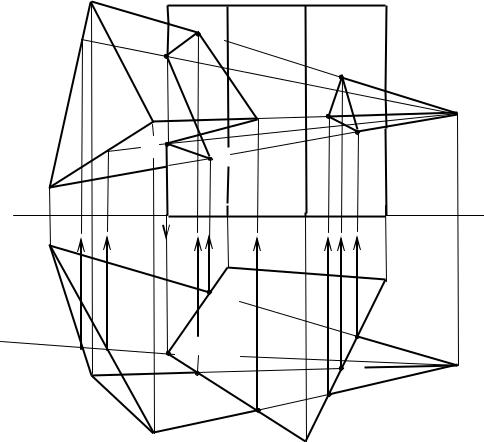
Рассмотрим случай полного проницания одного многогранника другим. На рис. 8.8 показано построение линии пересечения прямой четырехугольной призмы с пирамидой.

Призма своим основанием стоит на горизонтальной плоскости проекций H. Горизонтальные проекции ее вертикальных ребер являются точками. Грани боковой поверхности призмы представляют собой отсеки горизонтально - проецирующих плоскостей. Линия пересечения многогранников определяется по точкам пересечения ребер каждого из них с гранями другого многогранника. Так, ребро SA (sa, s' a' ) пирамиды пересекается с двумя вертикальными гранями призмы: с одной - в точке 1, 1' и со второй - в точке 2, 2'. Ребро sb, s' b' пересекает две вертикальные грани призмы в точках 33' и 44' ;ребро sc, s' c' - в точках ъ\=55' и 66'. Из четырех вертикальных ребер призмы только одно ребро пересекает пирамиду. Так как грани пирамиды являются плоскостями общего положения, то построение точек пересечения ребра призмы с гранями пирамиды производится по известной схеме (см. раздел 8.2.2.). Через это ребро и вершину пирамиды проводим вспомогательную горизонтально – проецирующую плоскость . Для плоскости проведен горизонтальный

след н через точки s и e. Плоскость пересекает две грани пирамиды : грань SBC по прямой MS (ms, m's' ) и грань SAC по прямой NS (ns, n's' ). Эти прямые пересекают ребро призмы в точках 77' и 88'. Теперь остается соединить точки, принадлежащие линии пересечения многогранников с учетом видимости и исходя из принадлежности этих точек одним и тем же граням.

b′	35

m′			′	3′
		7
						4′
		a′		1′	2′	s′
	n′	8′		5′		6′
c′			e′	k′	u′	r′
x
						o
c				k
				5		r

αн	m	n
		b

	6
e≡7≡8	s
4
3
2
1

a	u

Рис. 8.8–Взаимное пересечение призмы и пирамиды

. Получаем две линии пересечения многогранников. Одна из них представляет собой пространственный многоугольник 137581, 1'3'7'5'8'1', другая – треугольник 246, 2'4'6'.

Отрезки 24, 2'4' и 26, 2'6' линии пересечения 246, 2'4'6' видимы во фронтальной проекции. Они принадлежат видимым граням призмы и пирамиды. Отрезок 46, 4'6' является невидимым во фронтальной проекции, так как этот отрезок принадлежит видимой в этой проекции грани призмы и невидимой грани sbc, s'b'c' пирамиды. На фронтальной проекции видимы отрезки 13, 1'3' и 18, 1'8' второй линии пересечения, а отрезки 37, 3'7', 75, 7'5' и 58, 5'8' этой линии невидимы.

9.КРИВЫЕ ЛИНИИ И ПОВЕРХНОСТИ

9.1.Кривые линии

Кривую линию можно представить себе как след движущейся точки на плоскости или в пространстве. Примером служат известные из курса черчения средней школы спираль Архимеда и цилиндрическая винтовая линия.

Кривая линия может быть также получена в результате взаимного пересе-

чения поверхностей (например, цилиндрической и конической) или при пересечении поверхности плоскостью (например, окружность, получающаяся при

36

пересечении сферы плоскостью). В ряде случаев кривая линия представляет собой геометрическое место точек, отвечающих определенным для этой кривой условиям (окружность, эллипс, гипербола и т.п.).

Кривая линия определяется положениями составляющих ее точек. Точки кривой определяются их координатами.

Кривые линии, все точки которых принадлежат плоскости, называют плоскими. Примерами плоских кривых линий являются окружность, эллипс, спираль Архимеда.

Кривые линии, все точки которых не принадлежат плоскости, называют пространственными. Примерами пространственных кривых служат винтовая линия, линия пересечения боковых поверхностей прямых круговых цилиндра и конуса.

Пространственная кривая проецируется в виде плоской, плоская кривая - так же в виде плоской или в виде прямой линии, если кривая находится в плоскости, перпендикулярной плоскости проекций.

Способы образования кривых линий могут быть различны. Одни кривые линии образуются по определенному закону - закономерные кривые; образование других носит опытный, эмпирический характер - это незакономерные кривые.

Закономерные кривые линии могут быть заданы графически и аналитически, т.е. уравнениями. Незакономерные кривые задаются только графически на чертеже.

Закономерные кривые линии разделяются на алгебраические, т.е. определяемые в декартовых координатах алгебраическими уравнениями и трансцендентные, т.е. определяемые неалгебраическими уравнениями. Порядком алгебраической кривой называют степень ее уравнения. Например, эллипс является кривой второго порядка, так как в его уравнении переменные x и y

имеют второй порядок:

x2 / a2 + y2 / b2 = 1 .

Графически порядок плоской кривой линии характеризуется наибольшим числом точек ее пересечения с прямой линией. Порядок пространственной алгебраической кривой линии характеризуется наибольшим числом точек ее пересечения с плоскостью общего положения. Проекции кривых в общем случае представляются кривыми того же или более низкого порядка.

9.2. Кривые поверхности. Поверхности вращения

9.2.1. Образование и задание поверхностей.

В начертательной геометрии пользуются, главным образом, кинематическим способом образования поверхностей. При этом способе поверхность рассматривается как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Поверхность, образованная при наличии такого закона, называется закономерной поверхностью, в отличие от незакономерной поверхности.

37

Линию, производящую поверхность, в каждом ее положении называют образующей. Образующая обычно указывается в ряде ее положений. Говорят: "образуюшие", "проведем образующую" и т.п., понимая под этим различные положения образующей. Образующая линия может быть прямой или кривой. Поверхность, которая может быть образована прямой линией, называется линейчатой поверхностью. Линейчатая поверхность представляет собой геометрическое место прямых линий. Поверхность, для которой только кривая линия может быть образующей, называется нелинейчатой поверхностью.

От вида образующей и закона ее перемещения зависит форма (вид) кинематической поверхности. Закон перемещения в пространстве образуюшей удобно задавать неподвижными кривыми, которые называют направляющими линиями кинематической поверхности

.На любой кинематической поверхности можно выделить два семейства кривых линий: семейство образующих и семейство направляющих. Из семейств этих линий можно составить каркас кинематической поверхности.

Совокупность основных параметров поверхности, которые определяют ее задание, называют определителями поверхности. Например, определителем конуса вращения могут быть ось и образующая или вершина конуса и направляющая линия. Определителями цилиндра вращения могут быть ось и образующая (прямая или кривая) или ось и направляющая.

Каждая поверхность может быть образована различными способами. Так, например, поверхность кругового цилиндра (рис. 9.1) может быть образована вращением прямолинейной образующей l вокруг оси, ей параллельной или движением образующей окружности m, центр которой o перемещается по оси цилиндра, а плоскость окружности остается все время перпендикулярной к оси.

o2

m2

o1

m1

	o
l1	l3
l2

Рис.9.1- Образование поверхности кругового цилиндра

Из всех возможных способов образования поверхности необходимо выбирать такие, которые являются наиболее простыми и более удобными для решения данной задачи.

38

Задание поверхности на чертеже проекциями ее определителя обеспечивает обратимость чертежа, но не дает наглядности изображения. Для большей наглядности изображения поверхности в ряде случаев используют ее очерки - границы видимости на плоскостях проекций. Очерком данной поверхности называют линию пересечения с плоскостью проекций проецирующей поверхности (цилиндрической или конической, в зависимости от вида проецирования), обертывающей данную поверхность. Обертывающие проецирующие цилиндр или конус касаются данной поверхности по кривой линии, которую называют контурной линией. Очевидно, очерк поверхности является проекцией контурной линии.

9.2.2. Поверхности вращения.

Поверхностью вращения называется поверхность, которая получается от вращения какой-либо образующей вокруг неподвижной оси. Образующая может быть как пространственной, так и плоской кривой, в частном случае прямой линией. В состав определителя поверхности вращения входят образующая, ось вращения и условие о том, что эта образующая вращается вокруг оси.

На рис. 9.2 показана поверхность, образованная вращением плоской кривой ABC вокруг оси. Каждая точка образующей при вращении вокруг оси описывает окружность с центром на оси вращения. Эти окружности называют параллелями. Плоскость параллелей перпендикулярна к оси поверхности. Таким образом, параллели без искажения проецируются на плоскость, перпендикулярную к оси вращения. Наибольшую и наименьшую параллели называют соответственно

экватором и горлом. Плоскости,

проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность - меридианами. Меридиональную плоскость, параллельную плоскости проекций V, принято назы-

вать главной меридиональной

плоскостью, а линию ее пересечения с поверхностью вращения -

главным меридианом. На рис. 9.2

a′ o1′

		b′	d′	b1′
x			o′			o
	c′

c	b	a	o≡o1

d

Рис. 9.2- Образование поверхности вращения

39

ось поверхности вращения параллельна плоскости V, главный меридиан проецируется на плоскость V без искажения. Параллели данной поверхности вращения проецируются без искажения на плоскость H. Итак, на рис. 9.2 поверхность вращения задана проекциями ее оси OO1 , проекциями главного меридиана (очерк поверхности на плоскости V ) и экватора (очерк поверхности на плоскости H ).

Чтобы выделить какую – либо точку D на поверхности вращения, выбираем ее фронтальную проекцию d', после чего при помощи параллели BB1 , проведенной на уровне точки D, легко построить горизонтальную проекцию точки D - d. На рис. 9.2 точка D предполагается видимой во фронтальной проекции.

Рассмотрим некоторые из поверхностей, образуемые вращением

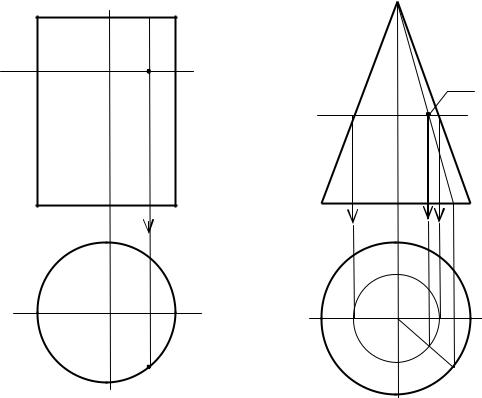
1)цилиндр вращения образуется вращением прямой вокруг параллельной ей оси (рис. 9.1). На рис. 9.3, а) изображен прямой круговой цилиндр;

2)конус вращения образуется вращением прямой вокруг пересекающейся с ней оси. На рис. 9.3, б) дан чертеж прямого кругового конуса.

αv

d ′

d ′

αv

d

а)	d	б)

Рис. 9.3–Комплексный чертеж цилиндра и конуса

Рассматриваемые поверхности (рис. 9.3) можно отнести и к классу линейчатых поверхностей, так как они образованы движением прямой линии.

Построение точки D на цилиндре или конусе можно выполнить при помощи плоскости, пересекающей эти поверхности по параллелям (окружностям) или при помощи прямолинейной образующей.

40

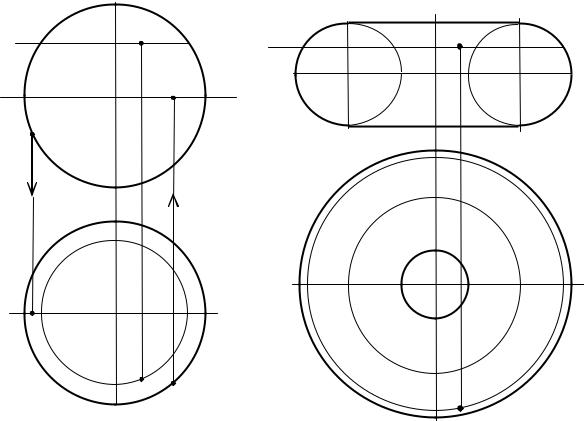
Рассмотрим поверхности, образуемые вращением окружности вокруг ее диаметра:

1)сфера образуется вращением окружности вокруг ее диаметра (рис. 9.4 а),

2)тор образуется вращением окружности вокруг оси, лежащей в плоскости окружности, но не проходящей через ее центр. При этом, если ось проходит вне окружности, такой тор называют кольцом (рис. 9.4 б).

Построение точки как на сфере, так и на торе производят с помощью

окружности, которая получается при пересечении плоскости, проходящей через эту точку, с поверхностью (рис. 9.4).

αV

d′

αV

d′

b′

a′

a

d
b	d
а)	б)

Рис. 9.4–Комплексный чертеж сферы и тора

Поверхности цилиндра, конуса и сферы являются поверхностями второго порядка, максимальное число точек пересечения каждой из этих поверхностей с прямой линией равно двум. Тор является поверхностью четвертого порядка, максимальное число точек пересечения тора с прямой линией равно четырем.