
Shpory
.docx|
1. Законы Ньютона В фундаменте динамики лежат 3 закона Ньютона.
Масса – мера инертности тела (способность тела сопротивляться изменению состояния). Первый закон Ньютона выполняется только в инерциальных системах отсчёта.
Третий закон Ньютона выполняется только при непосредственном соприкосновении двух тел, а так же при взаимодействии находящихся на некотором расстоянии друг от друга покоящихся тел.
|
2. Кинетическая энергия вращающегося тела. Момент инерции. При вращении твёрдого тела вокруг оси каждая элементарная точка с массой mi совершает движение с угловой частотой, равной: ω= Тогда кинетическая энергия будет вычисляться по формуле: E= I= I= Моменты инерции некоторых тел:
|
3. Момент импульса. Момент силы. Для описания сложного движения материальных тел вводится понятие момента импульса. Момент
импульса относительно точки это
векторная физ. величина, вычисляется
по формуле: (рисунок)
Момент
импульса относительно оси вращения
это скалярная физическая величина,
равная проекции
(рисунок)
Для
твёрдого тела проекция момента импульса
равна:
Для описания движения вращающегося тела вводится также понятие момента силы: (рисунок)
Для проекции
момента силы на ось Z
можно записать:
|
4. Уравнение движения вращающегося тела. Для описания движения вращающегося тела вводится понятие момента силы: (рисунок)
Для проекции
момента силы на ось Z
можно записать:
|
|
5. О закономерностях изменения оси вращения вращающегося тела. (рисунок из конспекта) Пусть
диск вращается вдоль оси Z
с угловой скоростью
1.
Направление вектора
2. Поворот оси вращения в плоскости XZ можно расценивать как дополнительное вращение вокруг оси Y L= Определим N след. Образом:
|
6. Вращающийся волчок. (рисунок из конспекта) Если
бы на волчок не действовали никакие
силы, то:
m
[
|
7. Преобразования Галилея. (рисунок из конспекта: две системы координат) Пусть
Концепция абсолютного времени: Рассмотрим
2 точки
Найдем
расстояние между точками в системе
Закон преобразования скоростей
Дифференцируем
закон сложения скоростей, получаем
законы механики
Ньютона удовлетворяют принципу
относительности. Однако, когда в разных
системах координат стали рассматривать
распространение электромагнитного
поля, описанного уравнением Максвелла,
оказалось, что уравнение не удовлетворяют
принципу относительности. Уравнения
Максвелла удовлетворяют принципу
относительности тогда, когда скорость
электромагнитной волны была одинакова
во всех системах отсчета, независимо
от скорости
|
8. Преобразования Лоренца Когда
в разных системах координат стали
рассматривать распространение
электромагнитного поля, описанного
уравнением Максвелла, оказалось, что
уравнение не удовлетворяют принципу
относительности. Уравнения Максвелла
удовлетворяют принципу относительности
тогда, когда скорость электромагнитной
волны была одинакова во всех системах
отсчета, независимо от скорости
Требования к преобразованиям координат
Уровняем в размерностях пространственные и временные координаты
Совместим
Условие
постоянства скорости света в
Уравнение
фронта световой волны имеет вид:
Преобразования Лоренца отличаются от Галилеевских. В преобразованиях Галилея пространственные и временные интервалы абсолютны и не зависят от движения СО. Согласно преобразованиям Лоренца наблюдатели, находящиеся в разных СО, видят (измеряют) один и тот же интервал разным. |
|
9. Пространственные и временные интервалы в различных СО (рисунок из конспекта: две системы координат)
Пусть
наблюдатель в движущейся СО измеряет
длину находящегося там стержня, отмечая
координаты его концов
Для
корректного измерения длины стержня,
его начало и конец должны быть определены
в один и тот же момент времени:
Пусть
системы
(рисунок из конспекта: две системы координат)
Пусть в
Чтобы
исключить зависимость временных
интервалов от координат, положим, что
2 события происходят в одной точке в
системе
Как следует из выше приведенного материала, в системе покоя пространственный интервал имеет максимальную длину (собственная длина). Временной интервал в системе покоя, между событиями, происходящими в одной точке – минимален (собственное время). |
10. Закон сохранения импульса. Импульс
где m0 – масса покоя тела, а m – релятивистская масса. Экспериментально было установлено, что при взаимодействии двух тел массами m1 и m2 изменение их скоростей удовлетворяет следующему уравнению: M1Δ Для изолирования системы, на которую не действуют никакие силы, или равнодействующая всех сил равна нулю, суммарный момент импульса равен постоянной величине. Если система состоит из n тел, то:
|
11. Работа и кинетическая энергия. Пусть
на тело массой m
действует сила
Как следует из полученной формулы для A – она зависит от формы траектории.
Таким
образом, работа, произведенная силой
|
12. Работа и потенциальная энергия. В отличие от массы, которая является свойством материального объекта, понятие силы представляет собой эффект воздействия на этот объект других материальных объектов, а задачей физики является описать эволюцию этого тела в пространстве и во времени. Однако на практике зачастую оказывается затруднительным дать явный функциональный вид для силы, и в этом случае вводят понятие потенциальной энергии. Потенциальная
энергия – если она существует для
данного физического процесса, то по
определению она вводится следующим
образом:
(рисунок)
|
|
13. Сохранение полной механической энергии. Если мы имеем дело с силами, определяемыми через потенциальную энергию, то при совершении работы имеют место 2 эффекта:
В связи с этим можно сделать заключение, что изменение полной энергии равно нулю. ∆ При
малых скоростях:
Общий случай закона сохранения энергии (рисунок: наклонная плоскость)
|
14. Сохранение момента импульса. Нами уже установлено, что момент импульса сохраняется в отсутствие внешних сил, а полная энергия сохраняется в потенциальном силовом поле.
|
15. Кинетическая энергия движения по сложной траектории (с учётом момента импульса). Движение в поле центральной силы Силовое поле называется центральным, если сила, действующая на тело, направлена вдоль радиус-вектора. Когда сила направлена вдоль линии, соединяющей движущееся тело и силовой центр, в поле которого происходит движение (рисунки)
Для анализа сложного движения в поле центральной силы, разделим движение, связанное с изменением радиуса и движение связанное с поворотом на определенный угол. (рисунок)
|
16. Движение в поле сил, обратно пропорциональных квадрату расстояния. Потенциальная энергия полей консервативных сил, обратно пропорциональных квадрату расстояний:
|
|
|
|
|
|
|
17. Связанное состояние и движение по эллиптическим орбитам (эффективная потенциальная энергия). При движении в поле центральной силы, материальная частица массой m, может обладать различными скоростями, при этом в одних случаях система оказывается связанной, и движение происходит в ограниченной области, в других случаях частица может уйти на бесконечность.
(график) Связанное
состояние может быть только, если
полная энергия
Определение
критической скорости, при которой
произвольное тело массой m
может выйти за пределы силового поля
Пусть движение начинается в r=R Вне
зоны действия сил гравитации скорость
Следует
Эффективная потенциальная энергия. Полную энергию движущегося тела массой m в потенциальном поле U можно представить в виде:
При
движении в поле центральной силы
оказывается возможным рассматривать
процессы движения как одномерные,
анализируя только
Такой подход позволяет определить все характеристики движения системы
|
18. Движение планет. Законы Кеплера. Определим скорость, с которой движется частица, имеющая минимальную потенциальную энергию
Рассмотрим
более сложный случай, когда
Так
как линия
Предположим,
что
Частица
массы
(рисунок)
При
(рисунок) Для
окружности
Для
эллиптических орбит формула остается
такой же, только вместо
(рисунок) При
этом
(рисунок) За
время
|
19. Неинерциальные системы отсчёта. Центробежная сила. Сила Кориолиса (написать закон движения тела вокруг оси). (рисунок из конспекта)
Для
простоты рассмотрим случай, когда
Пусть
система
Выражение
в первых скобках – это скорость,
которую измеряет наблюдатель,
находящийся в системе
Закон движения можно получить из второго закона Ньютона
Для
того чтобы описать движение тела в
системе
Сила Кориолиса (рисунок) Центробежная
сила (рисунок)
|
20. Колебательное движение. Гармонические колебания. Колебательным
называется движение, которое полностью
повторяется через равные промежутки
времени – периоды колебания
Гармоническое
движение – такое движение, когда
смещение тела
Колебательные движения удобно описывать, взяв за основу потенциальную энергию тела Разложим
Выберем
|
|
21. Математический маятник. Крутильный маятник. (рисунок)
(рисунок)
|
22. Физический маятник. (рисунок)
Для
малых углов
|
23. Затухающие колебания. (рисунок) При движении имеет место диссипация энергии. Для описания движения необходимо ввести силу трения
(рисунок: график) Затухание колебаний определяется уменьшением амплитуды за период колебания
|
24. Вынужденные колебания. (рисунок)
Пусть
сила, действующая на шарик,
При действии внешней силы наступает момент, когда потери энергии на диссипацию компенсируются работой внешней силы. При этом устанавливается стационарный процесс колебаний, причем колебания происходят с частотой вынуждающей силы
Из
теории функции комплексного числа
следует, что комплексный знаменатель
можно представить в виде:
|
|
|
|
|
|
|
25. Волны. Волновое уравнение (фаза). Явление распространения колебаний в пространстве называется волновым движением или волной. Геометрическое место точек, до которых доходят колебания в данный момент времени называются волновым фронтом. Геометрическое место точек, колеблющихся с одинаковой фазой, называется волновой поверхностью. Уравнением волны называется уравнение, которое определяет смещение частицы среды в данной точке пространства в данный момент времени. Волновой процесс в общем случае описывается законом смещения атомов среды относительно положения равновесия.
Таким
образом, в точке x
имеет место колебание, которое τ секунд
назад было в точке
|
26. Скорость упругих волн в различных средах. Пусть данный цилиндр – маленький фрагмент твёрдого тела, по которому движется упругая волна. В плоскости x смещение атомов около положения равновесия равно ξ, в плоскости x+Δx – ξ+Δξ, причём Δξ может иметь разный знак.
Реакция
среды на распространение волны
определяется внутренним напряжением
В связи с тем, что атомы в твёрдых телах жёстко связаны друг с другом, волновой процесс имеет сложных характер. Пусть
основанию этого цилиндра сообщён
единственный импульс, тогда атомы
плоскости S
за время
За
В
объёме
Реакция вещества на внешнее воздействие (волну) определяется напряжением.
E – модуль Юнга.
Если в среде
атомы слабо связаны друг с другом и
она однородна, что
|
27. Энергия упругих волн. Распространяясь
по твёрдому телу, упругая волна
переносит энергию, которая состоит
из кинетической энергии движения
частиц среды и потенциальной энергии
деформации этой среды.
Выделим в среде объём V настолько малый, что все смещения внутри него можно считать одинаковыми.
При деформации твёрдого тела внешние силы совершают работу, которая переходит в потенциальную энергию деформации. Для
деформации цилиндра на величину x
к нему необходимо приложить силу
Элементарная
работа, необходимая для деформации
стержня на
Работа,
необходимая для деформации стержня
на dl
равна сумме элементарных работ на
этом участке
Применим эти рассуждения к распространению волны по твёрдому телу:
Наиболее
применимым в физике понятием является
плотность энергии
Таким
образом, энергия упругих колебаний
изменяется как
Средняя
плотность энергии по периоду колебаний:
Количество энергии, проходящее через данную площадь в единицу времени называется потоком энергии.
Интенсивностью
упругой волны называется среднее
значение вектора
|
28. Тепловое движение. Степени свободы. Тепловое движение – характеристика движения атомов или молекул среды, которые испытывают как упругие так и неупругие столкновения. Движение молекулы можно разделить на поступательное, вращательное и колебательное. 1.
При поступательном движении
энергетическое состояние молекулы
определяется тремя величинами
2.
Вращательное движение:
3.
При описании произвольного колебательного
движения его необходимо разделить на
простейшие колебания вдоль осей x,
y
и z.
В этом простейшем колебании есть 2 независимые друг от друга величины А и ω колебательное движение описывается шестью независимыми величинами, т.е. имеет 6 степеней свободы. Степенями свободы называются независимые друг от друга величины, описывающие состояние системы. Таким
образом, с учётом степеней свободы
энергию произвольной термодинамической
системы можно записать следующим
образом:
Для системы,
находящейся в состоянии термодинамического
равновесия:
|
|
29. Первое и второе начало термодинамики. Внутренняя энергия системы состоит из всех видов кинетической и потенциальной энергии всех компонент системы. Для
разряженного идеального газа
Внутренняя энергия является основной характеристикой системы и описывает её фазовое состояние. Для
любой термодинамической системы можно
записать ЗСЭ:
Первое начало термодинамики утверждает, что при переходе системы из одного состояния в другое изменение внутренней энергии равно разности между количеством теплоты Q и работой A, совершаемой системой над внешними телами.
Внешней положительной работой называется та работа, которую совершают силы со стороны термодинамической системы над внешними телами (например, расширяющийся газ двигает поршень вверх). Тепло, получаемое системой, считается положительным, а отдаваемое – отрицательным. Любая
тепловая машина, работающая циклически,
характеризуется коэффициентом
полезного действия (КПД), который
определяется как отношение совершаемой
за цикл работы к получаемому за этот
же цикл теплу.
Приняв
во внимание то, что
Из определения следует, что КПД не может быть больше единицы. Второе начало термодинамики может быть сформулировано несколькими способами: 1.
Энтропия изолированной системы не
может убывать.
2. Невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от менее нагретого тела к более нагретому. (формулировка Клаузиуса) 3. Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара. (формулировка Томсона)
|
30. Энтропия системы. Изопроцессы. При изопроцессах один из параметров состояния считается постоянным. Изохорный
процесс:
Изобарический
процесс:
Изотермический
процесс:
Адиабатический
процесс: система не обменивается
теплотой с окружающей средой ( (график всех процессов на PV ск). При переходе системы из одной термодинамической системы в другую промежуточные состояния могут быть как равновесными, так и неравновесными. Равновесные состояния характеризуются либо максимальной вероятностью состояния, либо минимальной энергией, либо и тем и другим. Будучи в неравновесном состоянии система через какое-то время, называемое временем релаксации, переходит в равновесное состояние. Термодинамическая
вероятность размещения N
частиц по n
состояниям определяется следующей
формулой:
Такую
ситуацию Больцман предложил описывать
с помощью энтропии.
S – энтропия наиболее вероятного состояния максимальна. |
31. Основное уравнение МКТ газов. (рисунок, круг) Импульс
, сообщенный стене в точке А равен
Число
столкновений ν этой молекулы со стенкой
в одну секунду равно
Для
всех N
молекул импульс P,
полученный сферой за одну секунду
будет равен
Тогда
давление
Из закона (1) можно получить законы Бойля-Мариотта, Шарля и Гей-Люссака. Наиболее
обобщающей является формула
Менделеева-Клайперона
|
|

 =m
=m =
=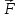
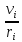
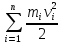 =
=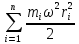 =
=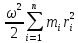 =
=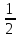 Iω2
=>
Iω2
=>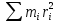 где I-момент
инерции.
где I-момент
инерции.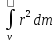
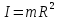


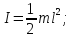

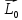 на ось.
на ось.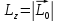
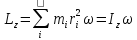 закон
движения вращающегося тела.
закон
движения вращающегося тела.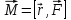 ,
,
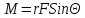
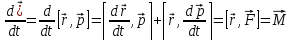 =>
=>

 Уравнение
движения вращающегося тела.
Уравнение
движения вращающегося тела.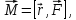
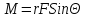
 =>
=>
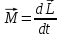
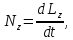
 =>
=>
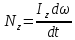 Уравнение
движения вращающегося тела.
Уравнение
движения вращающегося тела.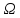 (ω – большое). Пусть в результате
какого-то воздействия ось повернулась
в плоскости XY
на угол
(ω – большое). Пусть в результате
какого-то воздействия ось повернулась
в плоскости XY
на угол

 =L
=L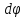 =L
ω
=L
ω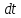 ;
;
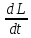 =
L
ω
=
L
ω - вдоль оси X
- вдоль оси X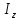
 ;
;
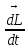 =
=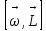
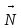 =
= ,
где h
– вектор, длина которого это расстояние
между точками приложения сил.
,
где h
– вектор, длина которого это расстояние
между точками приложения сил.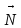 =
= =
=
 =
=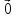 ,
,
 =const
=const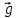 стремиться повернуть ось вниз, однако
ось вращения будет поворачиваться не
вниз, а перпендикулярно плоскости,
проходящей через ось z
и ось вращения волчка.
стремиться повернуть ось вниз, однако
ось вращения будет поворачиваться не
вниз, а перпендикулярно плоскости,
проходящей через ось z
и ось вращения волчка.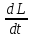 =[
=[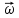 ,
,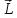 ]=
]=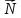

 =m[
=m[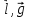 ]=ml[
]=ml[ ],
],
 =
=
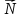 =
=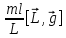
 =
= =[
=[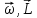 ]
- для вращающегося тела.
]
- для вращающегося тела.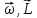 ]=
]=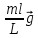 x
x
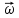 =-
=-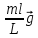 - частота прецессии.
- частота прецессии. движется относительно
движется относительно
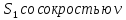
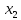 =
=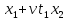 =
=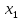 ,
,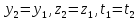
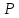 и
и
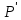 ,
в системе
,
в системе
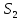
 и
и
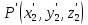 в системе
в системе
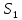
 и
и
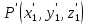
 :
:
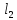 =
= =
=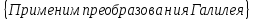 =
=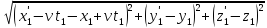 =
=
 =
=
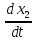 =
=

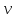 состемы отсчета:
состемы отсчета:
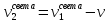 ;
;
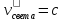
 состемы отсчета:
состемы отсчета:
 ;
;
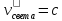
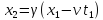
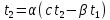
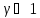 если
если
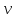 ⇾0,
⇾0,
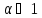 если
если ⇾0,
⇾0,
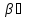 0
если
0
если
 ⇾0
⇾0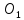 и
и
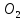 в
в
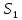 и
и
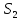 и в момент времени
и в момент времени
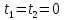 ,
,
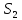 двинется со скоростью
двинется со скоростью
 и в этот же момент из
и в этот же момент из
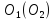 излучается сферический импульс света.
излучается сферический импульс света.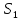 и
и
 может быть записано:
может быть записано:
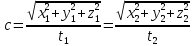
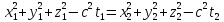
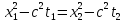 ,
,

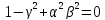 ,
,
 ,
,

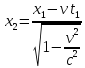 ,
,
 - преобразования Лоренца,
- преобразования Лоренца,
 - релятивийский корень
- релятивийский корень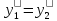 ,
,
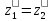
 =
= С
помощью преобразований Лоренца
определим длинну этого же стержня с
точки зрения
наблюдателя,
покоящегося в системе
С
помощью преобразований Лоренца
определим длинну этого же стержня с
точки зрения
наблюдателя,
покоящегося в системе
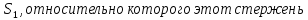 движется со скоростью
движется со скоростью

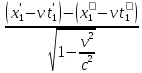 ,
где
,
где
 определения координат стержня.
определения координат стержня.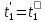 .
.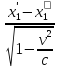
 =
=
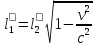
 и
и
 совмещены началами координат и в них
находятся синхронизированные часы.
Система
совмещены началами координат и в них
находятся синхронизированные часы.
Система
 двинулась со сокоростью
двинулась со сокоростью
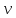 относительно
относительно
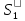
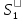 в
точке
в
точке
 и
и
 произошли 2 события интервал между
которыми равняется
произошли 2 события интервал между
которыми равняется
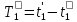 .
Каким будет этот интервал, измерянный
часами в системе
.
Каким будет этот интервал, измерянный
часами в системе
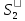 ?
Интервал может быт определен с помощью
преобразований Лоренца:
?
Интервал может быт определен с помощью
преобразований Лоренца: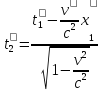
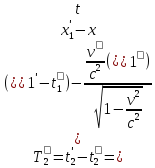
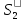
 – таким образом,
наблюдатель в системе
– таким образом,
наблюдатель в системе
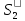 ,
измеряющий интервал по своим часам,
обнаружит, что интервал больше чем в
системе
,
измеряющий интервал по своим часам,
обнаружит, что интервал больше чем в
системе
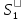 :
:
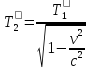
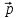 =m
=m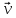 .
Для скоростей, близких к скорости
света:
.
Для скоростей, близких к скорости
света:
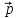 =
=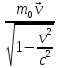
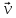 1=-M2Δ
1=-M2Δ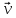 2,
Δ
2,
Δ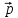 1=-Δ
1=-Δ 2,
2,
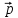 1+
1+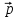 2=const
2=const =const
=const (рисунок)
(рисунок)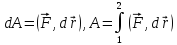 (рисунок)
(рисунок)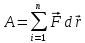 ,
,
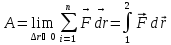
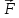 - результирующая
сил
- результирующая
сил
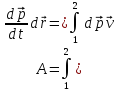 ,
,
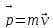
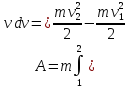
 ,
,
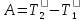
 ,
может быть определена как увеличение
кинетической энергии тела, движущегося
под действием сил.
,
может быть определена как увеличение
кинетической энергии тела, движущегося
под действием сил.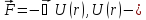 энергия,
через которую определяется сила.
энергия,
через которую определяется сила.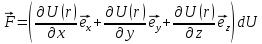
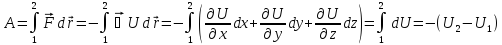 – из полученной
формулы следует, что работа, произведенная
силой, определяется только положениями
начальной и конечной точек, и не зависит
от формы пути. Этот факт условием
(необходимым и достаточным) для
существования потенциальной энергии.
Соответствующие силы F
определяемые через эту энергию
называются консервативными.
– из полученной
формулы следует, что работа, произведенная
силой, определяется только положениями
начальной и конечной точек, и не зависит
от формы пути. Этот факт условием
(необходимым и достаточным) для
существования потенциальной энергии.
Соответствующие силы F
определяемые через эту энергию
называются консервативными.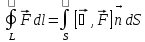 ,
т.к.
,
т.к.
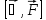 - ротор равен нулю, это значит что линии
поля прямые.
- ротор равен нулю, это значит что линии
поля прямые.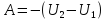

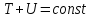
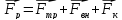
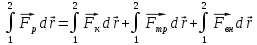
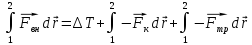
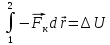
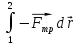 – сила, действующая
со стороны тела на плоскость. Действие
этой силы состоит в том, что при движении
тела по поверхности происходит
изменение кинетической и потенциальной
энергии атомов входящих в состав тела
и плоскости – это диссепация механической
энергии в тепловую.
– сила, действующая
со стороны тела на плоскость. Действие
этой силы состоит в том, что при движении
тела по поверхности происходит
изменение кинетической и потенциальной
энергии атомов входящих в состав тела
и плоскости – это диссепация механической
энергии в тепловую.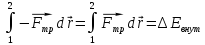
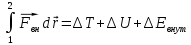 – полный закон
сохранения энергии.
– полный закон
сохранения энергии.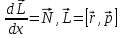
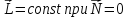
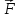 =
= ,
,
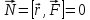
 ,
,
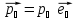
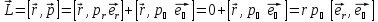

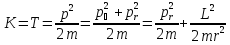 ,
,

 ,
,
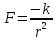
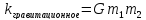

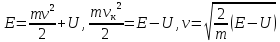

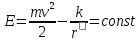
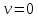 ,
а расстояние равно ∞
,
а расстояние равно ∞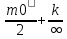 =0=
=0=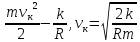
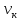 - не зависит от траектории движения
тела.
- не зависит от траектории движения
тела.
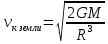 – вторая космическая скорость.
– вторая космическая скорость.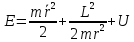
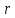 и
и
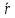 .
Кроме того полную энергию можно
записать в виде:
.
Кроме того полную энергию можно
записать в виде:
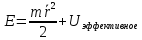 ,
,
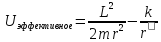
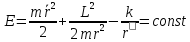
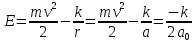
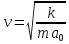
 ,
но
,
но
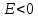
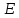 пересекает
пересекает
 в двух точках, то очевидно, что движение
будет осуществляться в поле силового
центра, таким образом, что расстояние
до него будет изменяться от минимального
в двух точках, то очевидно, что движение
будет осуществляться в поле силового
центра, таким образом, что расстояние
до него будет изменяться от минимального
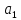 до
до
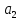 .
. и
и
 - точки поворота, в которых скорость
- точки поворота, в которых скорость
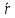 равна нулю, тогда значение этих точек,
можно найти из уравнения
равна нулю, тогда значение этих точек,
можно найти из уравнения
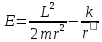
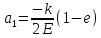 ,
,
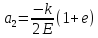 ,
,
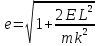
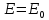 ,
,
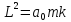 ⇒
⇒ ,
,
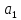

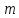 движется
в поле силового центра, таким образом,
что ее расстояние меняется от
движется
в поле силового центра, таким образом,
что ее расстояние меняется от
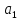 до
до
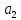 ,
центр находится внутри траектории.
Такой траекторией является эллипс.
,
центр находится внутри траектории.
Такой траекторией является эллипс.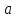 – большая полуось.
– большая полуось.
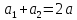 ,
тогда
,
тогда
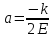 ,
,
 .
В ситуации, когда
.
В ситуации, когда
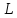 – максимален,
– максимален,
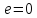 – движение по окружности
– движение по окружности ,
,
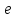 –
эксцентриситет
–
эксцентриситет
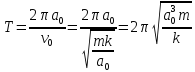
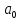 ставится большая полуось эллипса.
Полная скорость
ставится большая полуось эллипса.
Полная скорость

 ,
,
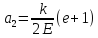 ,
,
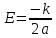 ,
,
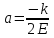 ,
,
 ,
,
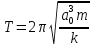
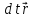 проходит
проходит
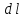
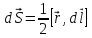 ,
,
 ,
,
 ,
,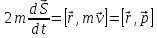
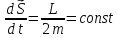 ⇒
за равные промежутки
времени радиус вектор, характеризующий
положение материальной точки ,
«выметает» равные площади. Таким
образом, если подставить
⇒
за равные промежутки
времени радиус вектор, характеризующий
положение материальной точки ,
«выметает» равные площади. Таким
образом, если подставить
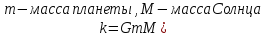 )
мы получим законы, управляющие движением
планет в солнечной системе, которые
сформулировал Кеплер следующим
образом:
)
мы получим законы, управляющие движением
планет в солнечной системе, которые
сформулировал Кеплер следующим
образом:
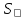 движется поступательно относительно
движется поступательно относительно


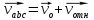 ,
,
 скорость движения точки О системы
скорость движения точки О системы
 (переносная
скорость).
(переносная
скорость).
 скорость точки M
относительно
S
скорость точки M
относительно
S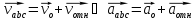
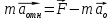 ,
,
 сила
инерции, которую надо учитывать при
описании движения в неинерциальных
системах координат. Задачей физики
является определение траектории
движения тела, на которое действует
реальная сила.
сила
инерции, которую надо учитывать при
описании движения в неинерциальных
системах координат. Задачей физики
является определение траектории
движения тела, на которое действует
реальная сила.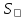 движется произвольным образом по
любой сложной траектории. Можно
показать, такое движение можно
представить как поступательное
движение начала системы координат
движется произвольным образом по
любой сложной траектории. Можно
показать, такое движение можно
представить как поступательное
движение начала системы координат
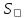 и вращательного движения вокруг
мгновенной оси проходящей через начало
координат.
и вращательного движения вокруг
мгновенной оси проходящей через начало
координат.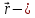 радиус-вектор
в системе
радиус-вектор
в системе
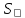 .
.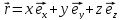 ,
,
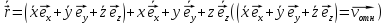
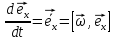 ,
,
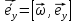 ,
,
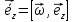
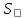 (относительно
него
(относительно
него
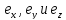 не меняются в пространстве)
не меняются в пространстве)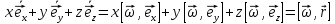
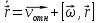 ,
,
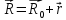
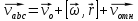
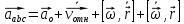
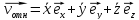


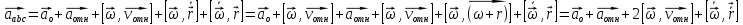
 - реальная сила
- реальная сила
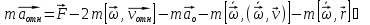 не инерциальная
система отсчета
не инерциальная
система отсчета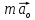 - связано с
ускорением движения системы
- связано с
ускорением движения системы

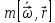 - обусловлено
переменной угловой скоростью вращения
- обусловлено
переменной угловой скоростью вращения - сила Кориолиса
- сила Кориолиса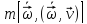 – центробежная
сила
– центробежная
сила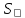 в уравнение движения необходимо
включить все силы инерции, возникающие
при движении
в уравнение движения необходимо
включить все силы инерции, возникающие
при движении
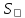

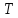
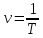 – частота,
– частота,
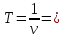
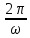
 описывается формулой
описывается формулой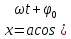 ),
где
),
где
 - начальная фаза
- начальная фаза в ряд Тейлора:
в ряд Тейлора: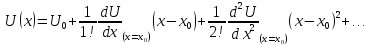
 ;
известно, что в точке равновесия
;
известно, что в точке равновесия
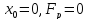 ⇒
⇒
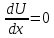
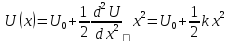
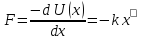 - квазиупругая
сила
- квазиупругая
сила
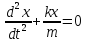 ,
,
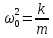
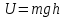
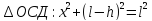 ,
,
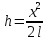 ,
,
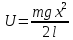
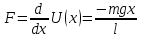

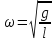 ,
,
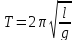
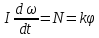
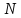 – момент сил
– момент сил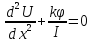
 ,
,

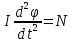



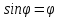
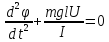
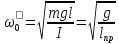 ,
,
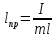 - длинна такого математического
маятника, период колебания которого
совпадает с периодом физического
маятника.
- длинна такого математического
маятника, период колебания которого
совпадает с периодом физического
маятника.
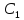 –
центр
качания физического маятника.
–
центр
качания физического маятника.


 ,
,
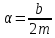 ,
,

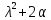 λ
λ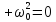

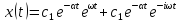
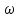 =
=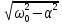
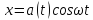 ,
,
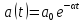

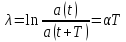 – логарифмический
дискремент затухания
– логарифмический
дискремент затухания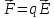
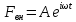
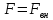
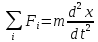 – способ описания
движения
– способ описания
движения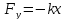 ,
,

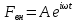

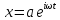
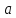 – амплитуда
– амплитуда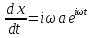 ,
,
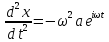
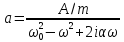
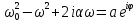
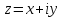 ,
,
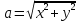 ,
,
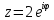
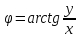
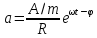 ,
,
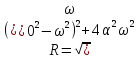 ,
,
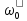 - частота собственных колебаний
- частота собственных колебаний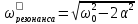 ,
,
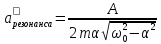
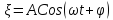
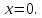
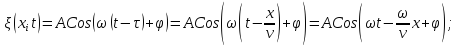

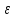 – деформация
твёрдого тела в точке x.
– деформация
твёрдого тела в точке x.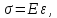 E
– модуль Юнга.
E
– модуль Юнга.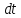 переместятся на
переместятся на
 .
.
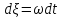
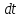 сформированная в результате воздействия
волна распространиться на расстояние
сформированная в результате воздействия
волна распространиться на расстояние
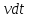 ,
где
,
где
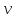 - фазовая скорость.
- фазовая скорость. имеет место деформационный процесс,
связанный с распространением волны.
имеет место деформационный процесс,
связанный с распространением волны.
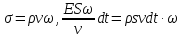
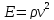
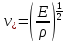 - скорость
распространения продольных волн.
- скорость
распространения продольных волн.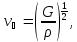 G
– модуль сдвига.
G
– модуль сдвига. k
– модуль всестороннего сжатия.
k
– модуль всестороннего сжатия.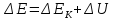
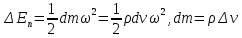

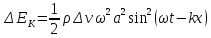

 этой силой:
этой силой:
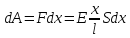
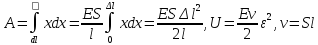
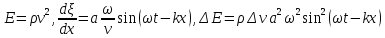
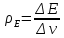
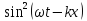
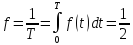
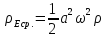
 Вектор Умова.
Вектор Умова.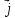 .
.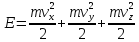
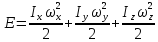

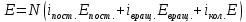
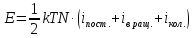
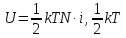 - энергия, приходящаяся на одну степень
свободы,
- энергия, приходящаяся на одну степень
свободы,
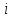 – число степеней свободы.
– число степеней свободы.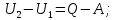
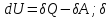 - приращение.
- приращение.
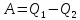 ,
получим
,
получим
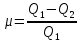
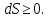

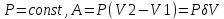
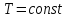
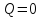 ).
Работа совершается за счёт внутренней
энергии термодинамической системы.
).
Работа совершается за счёт внутренней
энергии термодинамической системы.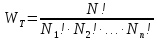
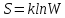
 .
.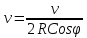 .
.
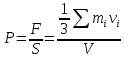

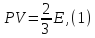 E
– полная кинетическая энергия всех
молекул.
E
– полная кинетическая энергия всех
молекул.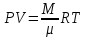 .
.