Линейная и квадратичная интерполяции

Иногда при интерполяции по заданной таблице при m>3 точек приме- няют квадратичную (n=3) или линейную (n=2) интерполяцию. В этом случае для приближенного вычисления значения функции f(x) в текущей точке xТ находят в таблице ближайшие к этой точке (i-1), i, (i+1)-й узлы из общей таблицы, строят интерполяционный многочлен Ньютона первой или второй степени по формулам.

Формулы численного интегрирования

Формулы для вычисления интеграла получают следующим образом. Область интегрирования [a, b] разбивают на m малых отрезков с шагом h=b-a/m. Значение интеграла по всей области равно сумме интегралов на отрезках. Выбирают на каждом отрезке 1 – 5 узлов и строят для каждого отрезка интерполяционный многочлен соответствующего порядка. Вычисляют интеграл от этого многочлена на отрезке. В результате получают выражение интеграла (формулу численного интегрирования) через значения подынтегральной функции в выбранной системе точек. Такие выражения называют квадратурными формулами.

Формула средних

Формула средних получается, если на каждом i-ом отрезке [xi-1, xi] взять один центральный узел xi-1/2 = xi - h/2, соответствующий середине отрезка. Функция на каждом отрезке аппроксимируется многочленом нулевой степени (константой) P0(x) = f(xi-1/2). Погрешность формулы средних имеет второй порядок по h. .

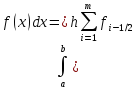Формула трапеций

Формула трапеций получается при аппроксимации функции f(x) на каждом отрезке интерполяционным многочленом первого порядка, т. е. прямой, проходящей через точки x(i-1) f(i-1), x(i) f(i). Площадь криволинейной фигуры заменяется площадью трапеции с высотами f(i-1) f(i) и основанием h. Погрешность формулы трапеций в два раза больше, чем погрешность формулы средних.

Формула Симпсона

Формула Симпсона получается при аппроксимации функции f(x) на каждом отрезке интерполяционным многочленом второго порядка (параболой) c узлами x(i-1), x(i-1/2), x(i). Погрешность формулы Симпсона имеет четвертый порядок по h. .

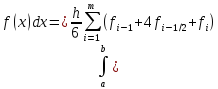Формулы Гаусса

При построении предыдущих формул в качестве узлов интерполяционного многочлена выбирались середины или концы интервала разбиения. При этом оказывается, что увеличение количества узлов не всегда приводит к уменьшению погрешности. Суть методов Гаусса с n узлами состоит в таком расположении этих n узлов интерполяционного многочлена на отрезке x(i-1), x(i), при котором достигается минимум погрешности квадратурной формулы. Детальный анализ показывает, что узлами, удовлетворяющими такому условию, являются нули ортогональнoго многочлена Лежандра n-й степени. Для n=2 узлы на отрезке x(i-1), x(i) должны быть выбраны следующим образом: 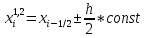. И соответствующая формула Гаусса с двумя узлами имеет вид: . Порядок погрешности этой формулы 4-ый. Для n=3 узлы выбираются следующим образом: 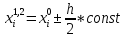. и соответствующая формула Гаусса с тремя узлами имеет вид: . Порядок погрешности этой формулы шестой. особенно широко применяются для вычисления несобственных интегралов специального вида, когда подынтегральная функция имеет достаточно высокие производные.