СЛАУ

СЛАУ. Основные понятия и определения

Обычно СЛАУ записывается в виде: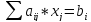 или 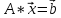(A - матрица, x,b – вектор-столбцы). Известно, что если определитель матрицы , то СЛАУ имеет единственное решение. В противном случае решение либо отсутствует (если 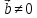), либо имеется бесконечное множество решений (если 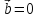). Важно чтобы задача была корректной, т. е. чтобы при малых погрешностях правой части 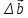и (или) коэффициентов 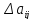погрешность решения также оставалась малой. Признаком некорректности, или плохой обусловленности, является близость к нулю определителя матрицы. Плохо обусловленная система двух уравнений геометрически соответствует почти параллельным прямым. Точка пересечения таких прямых (решение) при малейшей погрешности коэффициентов резко сдвигается. Корректность СЛАУ характеризуется числом 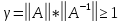. Чем дальше 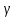от 1, тем хуже обусловлена система. Обычно при 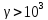система некорректна и требует специальных методов решения - методов регуляризации. Методы решения СЛАУ делятся на прямые и итерационные. Прямые методы дают достаточно точное решение за конечное число арифметических операций и используются для хорошо обусловленных СЛАУ небольшого порядка (метод Гаусса для СЛАУ общего вида, его модификация для трехдиагональной матрицы – метод прогонки и метод квадратного корня для СЛАУ с симметричной матрицей). Итерационные методы основаны на построении сходящейся к точному решению 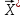рекуррентной последовательности векторов. Итерационные методы выгодны для систем большого порядка n>100, а также для решения плохо обусловленных систем (одношаговые методы простой итерации и Зейделя).

Метод Гаусса

Метод основан на приведении с помощью преобразований, не меняющих решение, исходной СЛАУ с произвольной матрицей к СЛАУ с верхней треугольной матрицей. Этап приведения к системе с треугольной матрицей называется прямым ходом метода Гаусса. Решение системы с верхней треугольной матрицей находится по формулам, называемым обратным ходом метода Гаусса. Прямой ход метода Гаусса осуществляется следующим образом: вычтем из каждого m-го уравнения (m=2, 3,.., n) первое уравнение, умноженное на , и вместо m-го уравнения подставим полученное. В результате в матрице системы исключаются все коэффициенты 1-го столбца ниже диагонального. Затем, используя 2-е полученное уравнение, аналогично исключим элементы второго столбца (m=3, 4,.., n) ниже диагонального и т. д. Такое исключение называется циклом метода Гаусса. Проделывая последовательно эту операцию, мы приходим к верхней треугольной матрице. При указанных операциях решение СЛАУ не изменяется. На каждом шаге преобразований прямого хода элементы матриц изменяются по формулам прямого хода метода Гаусса. Если в ходе расчетов по данному алгоритму на главной диагонали окажется нулевой элемент, то произойдет сбой. Для того чтобы избежать этого, следует каждый цикл начинать с перестановки строк.

Метод прогонки

Многие задачи (например, решение дифференциальных уравнений 2-го порядка) приводят к необходимости решения СЛАУ с трехдиагональной матрицей (главная диагональ и 2-е рядом). В этом случае расчетные формулы метода Гаусса значительно упрощаются. После исключения поддиагональных элементов в результате прямого хода метода Гаусса (Прямой ход метода Гаусса осуществляется следующим образом: вычтем из каждого m-го уравнения (m=2, 3,.., n) первое уравнение, умноженное на 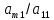, и вместо m-го уравнения подставим полученное. В результате в матрице системы исключаются все коэффициенты 1-го столбца ниже диагонального. Затем, используя 2-е полученное уравнение, аналогично исключим элементы второго столбца (m=3, 4,.., n) ниже диагонального и т. д. Такое исключение называется циклом метода Гаусса.) и последующего деления каждого уравнения на диагональный элемент систему можно привести к виду: . кси и кпд вычисляются по формулам. Когда такое преобразование (прямой ход) сделано, формулы обратного хода метода Гаусса также упрощаются и имеют несколько другой вид. Достаточным условием того, что в формулах метода прогонки не произойдет деления на нуль и расчет будет устойчив относительно погрешностей округления, является выполнение неравенства 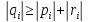(хотя бы для одного i должно быть строгое неравенство).

Метод квадратного корня

Метод предназначен для решения СЛАУ с симметричной матрицей. Этот метод основан на представлении такой матрицы в виде произведения трех матриц: 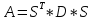, где D – диагональная с элементами 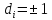, S – верхняя треугольная, 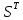– транспонированная нижняя треугольная. Матрицу S можно по аналогии с числами трактовать как корень квадратный из матрицы A, отсюда и название метода. Если матрицы S и D известны, то решение исходной системы сводится к последовательному решению трех систем – двух c треугольной и одной с диагональной матрицами. Решение систем ввиду треугольности матрицы S осуществляется по формулам, аналогичным обратному ходу метода Гаусса. Нахождение элементов матрицы S (извлечение корня из А) осуществляется по рекуррентным формулам. В этих формулах сначала полагаем k=1 и последовательно вычисляем 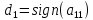; и все элементы первой строки матрицы S, затем полагаем k=2 и тд. Метод квадратного корня почти вдвое эффективнее метода Гаусса, т. к. полезно использует симметричность матрицы. Функция sign(x) возвращает – 1 для всех x<0 и +1 для всех x>0.

Метод простой итерации

В соответствии с общей идеей итерационных методов исходная система должна быть приведена к виду, разрешенному относительно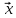: 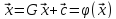, где G – матрица; 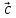– столбец свободных членов. При этом решение должно совпадать с решением исходной СЛАУ. Затем строится рекуррентная последовательность первого порядка . В начале вычислений задается некоторое начальное приближение 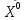, для окончания – некоторое малое eps. Получаемая по- следовательность будет сходиться к точному решению, если норма матрицы 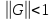. Привести исходную систему к виду 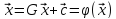можно различными способами. Если исходная матрица A имеет преобладающую главную диагональ то преобразование можно осуществить просто, решая каждое i-е уравнение относительно .

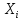Метод Зейделя

Метод Зейделя является модификацией метода простой итерации. Суть его состоит в том, что при вычислении очередного приближения 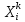используются уже вычисленные ранее значения. Такое усовершенствование позволяет ускорить сходимость итераций почти в два раза. Кроме того, данный метод может быть реализован на компьютере без привлечения дополнительного массива, так как полученное новое сразу засылается на место старого. Схема алгоритма аналогична схеме метода простой итерации, если заменить на 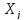и убрать строки .

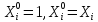Понятие релаксации

Методы простой итерации и Зейделя сходятся примерно так же, как геометрическая прогрессия со знаменателем 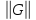. Если норма матрицы G близка к 1, то сходимость очень медленная. Для ускорения сходимости ис- пользуется метод релаксации. Суть его в том, что полученное по методу про- стой итерации или Зейделя очередное значение пересчитывается по формуле включающей в себя параметр релаксации 0<w<=2. Если w< 1 – нижняя релаксация, если w>1 – верхняя релаксация. Параметр подбирают так, чтобы сходимость метода достигалась за минимальное число итераций.

Нахождение обратных матриц

Матрица A-1 называется обратной по отношению к квадратной матрице A, если их произведение равно единичной матрице E. Если определитель матрицы A отличен от нуля (такие матрицы называются невырожденными или неособенными), то обратная матрица всегда существует. Обозначим искомую обратную матрицу n-го порядка X. Равенство AX=E, служащее определением обратной матрицы X может быть использовано для нахождения элементов обратной матрицы. Мы имеем систему 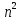линейных алгебраических уравнений для неизвестных элементов обратной матрицы, которую можно решить одним из методов решения систем линейных алгебраических уравнений. Вся эта система распадается на n групп независимых уравнений с n неизвестными в каждой. Все они имеют одну и ту же матрицу коэффициентов A, отличаясь лишь свободными членами. Таким образом, для нахождения элементов матрицы n-го порядка необходимо n раз решить систему линейных алгебраических уравнений n-го порядка. Так как все они имеют одну и ту же матрицу коэффициентов A, то при использовании метода Гаусса процедура прямого хода проводится только один раз. При этом решение этих n систем можно объединить в одной схеме, рассматривая одновременно n столбцов свободных членов.