Центр окружности, вписанных в треугольник лежит в точке пересечения биссектрис его углов.

Биссектриса – прямая, равноудалённая от углов треугольника.

A1x + B1 y + C = A2 x + B2 y + C				A1x + B1 y + C = ± A2 x + B2 y + C ,
A2	+ B2	A2	+ B2	A2	+ B2	A2	+ B2
1	1	2	2	1	1	2	2

± выбирается при подстановке координат точек, лежащих на сторонах угла. Если угол внутренний, то при подстановке координат точек в уравнение биссектрис, получаются разные знаки, так как они лежат в различных

полуплоскостях.	Если	угол	треугольника			внешний,	то	при подстановке
координат точек в уравнение биссектрис знаки будут различны.
3x + 4y +12 = 0		6x = 0			x = 0
3x − 4y −12 = 0		4y = −12			y −3
P(0,-3).						{x = -y
3x + 4y +12 = 0		7x + 7y = 0						x =12
			−12 = 0
4x +3y −12 = 0		4x −3y				x =12		y = −12
Q(12,-12).
Найдём уравнение биссектрисы угла, образованного прямыми 2 и 3.
4x +3y −12 = ± 3x − 4y −12
42 +32	32 + 42

4x +3y −12 = ±(3x − 4y −12)

+4x +3y −12 = 3y − 4y −12

1)x + 7y = 0 .

–4x +3y −12 = −3x + 4y +12

2) 7x − y − 24 = 0.
P(0,-3), Q(12,-12).
7 (−3) < 0	12 + 7 (−12) < 0	1)	– биссектриса внешнего угла.
3 − 24 < 0	7 12 +12 − 24 > 0	2)	– биссектриса внутреннего угла.

7x − y − 24 = 0 ― уравнение биссектрисы внутреннего угла при вершине R.

????????????????

1.6. Прямая и плоскость в пространстве

№1. Построить плоскости 1) 3x + 4y −6z −12 = 0, 2) z + y − 2 = 0, 3) 3y −7 = 0.

Решение:

1) 3x + 4y −6z =12,

x	+	y	−	z	=1,	a = 4, b = 3, c = −2.
4
	3		2

2) А=0 плоскость параллельна оси Ох.

27

y=0 z=2; z=0 y=2.

3)z+y=0, плоскость параллельна оси Ох и проходит через начало координат и ось Ох. В плоскости YOZ z=–y.

4)3у–7=0,

А=0, С=0 плоскость параллельна XOZ.

На оси Оу отсекается отрезок y = 73.

№2. Составить уравнение плоскости, перпендикулярной вектору n(2,−1,4) и

проходящей через точку М0(5, 2, –3). Лежат ли в этой плоскости точки Р(1, 2, – 1), Q(4, 5, 1) и R(–6, 2, 3).

Решение:

2(x −5) − (y − 2) + 4(z + 3) = 0 – уравнении плоскости, перпендикулярной

вектору n и проходящей через точку М0.

n(r − r0 ) = 0.

2x − y + 4z + 4 = 0 – общее уравнение плоскости.

P:2 1 − 2 + 4 (−1) + 4 = 0 P π,

Q:2 4 −5 + 4 1 +1 ≠ 0 Q π,

R:2 (−6) − 2 + 4 (−3) + 4 ≠ 0 Rπ.

Q и R находятся по разные стороны от π:

<0 для точек одного полупространства, >0 для точек другого полупространства.

Ответ: 2(x − 5) − (y − 2) + 4(z + 3) = 0, P π, Qπ, Rπ.

№3. Составить уравнения плоскостей по следующим данным:

1)плоскость перпендикулярна Oz и проходит через Р(1, –2, 3);

2)плоскость проходит через Оу и точку Q(4, 2, –5);

3)плоскость параллельна Ох и проходит через две точки R(1, 1, 2) и S(5, 3, –

2).

Решение:

1) n(0,0,1) или плоскость параллельна плоскости ХОУ. Cz + D = 0,

z = −DC = 3, z=3, z–3=0 C≠0. 2) 4A–5C=0A= 54 C,

54 Cx + Cz = 0, C≠0 54 x + z = 0 5x+4z=0.

3) A=0 By+Cz+D=0 R: B+2C+D=0,

	B = −D		3B + D		−	3	D	+ D		D .
S: 3B-2C+D=0 4B+2D=0		, C =		=		2			=
			2			2
	2									4

28

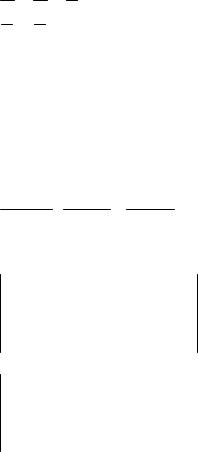
− D2 y − D4 z + z = 0, D≠0, 2y+z–4=0.

Ответ: z–3=0 C≠0, 5x+4z=0, 2y+z–4=0.

№4. составить уравнение плоскости, проходящей через точки М1(1, –2, 6), М2(5, –4, –2) и отсекающей равные отрезки на осях Ох и Оу.

Решение:

x

+

y

+

z

=1,

b

c

a

a = b

x

+

y

+ z

=1,

a

a

c

М1

→

1

−

2

+

6

=1

− 1

+

6

=

1

1

=

6

−1

a

a

c

a

c

a

c

М2

→

5

−

4

−

2

=1

1

−

2 =1

6

−1 −

2

=1

4

= 2 с=2

1

=3 −1 = 2

a

a

c

a

c

c

c

c

a

a = 12 .

x1 + 1y + 2z =1 4x + 4y + z − 2 = 0.

2 2

Ответ: 4x + 4y + z − 2 = 0.

№5*. Составить уравнение плоскости, походящие через три данные точки М1(x1, y1, Z1), М2(х2, у2, z2). Написать уравнение для случая M1 (1, 3, –2), М2(4, – 5, 6), М3(–3, 1, 2).

Решение:

M1M2 , M1M3 , M2 M3 лежат водной плоскости тогда и только тогда, когда они компланарны и их смешанное произведение равно 0.

x− x1

x2 − x1

x3 − x1

y − y1 y2 − y1 y3 − y1

z − z1

z2 − z1 = 0 z3 − z1

x −1 y − 3 z + 2						x −1 y − 3 z + 2				−8	8		3	8
3	−8	8		= 2		3	−8	8	= 2(x −1)			− (y −3)			+
− 4	− 2	4				− 2	−1	2		−1	2		− 2	2

29

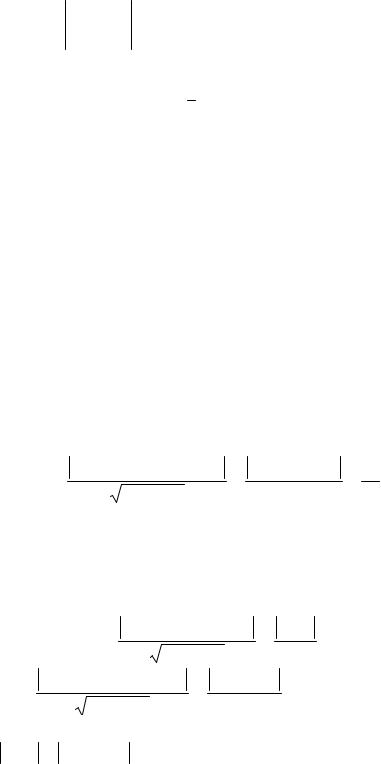
3−8

+(z + 2) − 2 −1 = −8(x −1) − 22(y − 3) −19(z + 2) = 0

8x + 22y +19z −36 = 0.

Аналитически составляем уравнение плоскости, проходящей через 1) 2 точки

параллельно вектору a , 2) одну точку параллельно 2-м неколлинеарным векторам.

№6. Дан тетраэдр А(2, –1, 3), В(1, –3, 5), С(6, 2, 5), D(3, –2, –5). Найти длину высоты, опущенной из вершины D на грань АВС.

Решение:

hD – расстоние от D до (АВС).

x − 2

y +1

z − 3

− 2

2

−1

2

−1

− 2

−1

− 2

2

= (x − 2)

− (y +1)

+ (z − 3)

= −10(x − 2) +10(y +1)

4

3

2

3

2

4

2

4

3

+ 5(z −3) = 0;

2(x–2)–2(y+1)–(z–3)=0;

2x–2y–z–3=0.

Находим расстояние от точки до плоскости:

D(3, –2, –5),

d = hD

= 2 3 − 2 (−2) + 5 −3

=

6 + 4 + 5 −3

=12 = 4.

4 + 4 +1

3

3

Ответ: hD = 4.

№7. На оси Oz найти точку, равноудалённую от двух плоскостей: 2x–2y+z–3=0, x+2y–2z+12=0.

Решение:

М(0, 0, z). d1 = 2 0 − 2 0			+ z − 3	=	z −3	;
		4 + 4	+1		3
d2	=	1 0 + 2 0 − 2z +12 =	− 2z +12 ;
		1 + 4 + 4	3

d1=d2:

z −3 = − 2z +12.

1) z − 3 = −2z +12 3z =15, z1=5, M1(0, 0, 5).

2) z − 3 = 2z −12 z2=9, M2(0, 0, 9). Ответ: z1=5, M1(0, 0, 5), z2=9, M2(0, 0, 9).

№8. Составить уравнение плоскости, параллельной плоскости 4x–4y+2z–3=0 и отстоящей от неё на 5 единиц.

Решение:

Уравнение плоскости, параллельной Ax+By+Cz+D=0 можно искать в виде

Ax+By+Cz+D1=0.

30

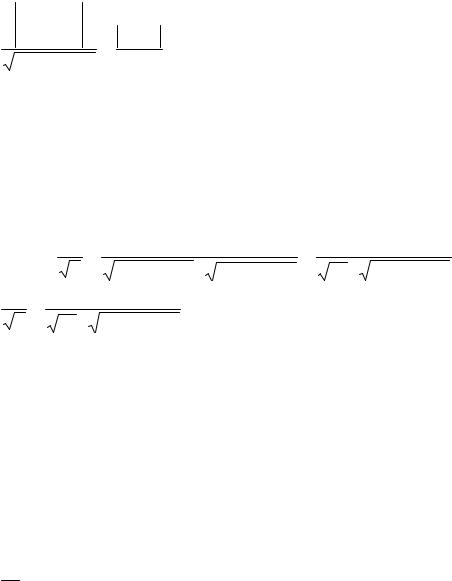
Уравнение искомой плоскости: 4x–4y+2z+D=0.						3) и определим
Возьмём			произвольную		точку первой плоскости (0,0,
расстояние от неё до второй плоскости.						2
3
2		+ D		3 + D =5 1) 3 + D = 5 D=30–3=27, D1=27;
	2		=
16 +16 +			4	6	6

2)			3 + D			= −5	D= –30–3= –33, D2= –33.
	6

Ответ: 4x–4y+2z+27=0, 4x–4y+2z–33=0.

№9. Через начало координат провести плоскость, перпендикулярную плоскости

5x–2y+5z–10=0 и образующую с плоскостью x–4y–8z+12=0 угол φ=45º.

Решение:

cosϕ =	1 =	1 1 − 4b −8c			=	1 − 4b −8c
	2	1 + b2 + c2 1 +16 + 64				81 1 + b2 + c2
1 =	1 − 4b −8c .
2	81	1 + b2 + c2	5(1 + c)
Из первого уравнения b =				.
			2

Возведём обе части уравнения в квадрат:

	1	=	(1 − 4b −8c)	2	,
	2		81(1 + b2 + c2 )
	81(1 + 25(1 + c)2			+ c2 ) = 2(1 −10(1 + c) −8c)2 или
			4

814 (29c2 + 50c + 29) = 2(−9 −18c)2 814 (29c2 + 50c + 29) = 2 92 (1 + 2c)2

29c2 + 50c + 29 =8(1 + 4c + 4c2 ) 29c2 + 50c + 29 = 32c2 + 32c + 8 3c2 −18c − 21 = 0

	c2	− 6c − 7 = 0
	c1 = 7,
	c2	= −1.
	b1	= 20,	условию задачи удовлетворяют 2 плоскости:
	b2	= 0.

1) x+20y+7z=0 и 2) x–z=0.

31

Если А=0 –2b+5с=0 b = 52 c.

−	4b −8c	=	1
81	b2 + c2		2

2(10c + 8c)2 =81(254 c2 + c2 )

c=0, b=0

Имеем a=b=c=0 плоскость не задают.

Ответ: 1) x+20y+7z=0 и 2) x–z=0.

№10*. Составить уравнение плоскости, проходящей через точку М0(х0,у0,z0) и перпендикулярной к двум пересекающимся плоскостям A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0. Написать уравнение для случая, когда М(2, –3, 1) и плоскости заданы уравнениями: 3x–y+2z–1=0, 4x+5y–3z+2=0.

Решение:

n1={A1 ,B1 ,C1} и n2={A2 ,B2 ,C2 } – векторы нормалей к плоскостям. Задача сводится к составлению уравнения плоскости, проходящей через данную точку и параллельную двум неколлинеарным векторам.

=

=

,

r

OM,

r0

OM0

(r

− r0 )n1 n2 = 0 – векторное уравнение (3 вектора

компланарны).

x − x0

y − y0

z − z0

A1

B1

C1

= 0, для конкретного случая

A2

B2

C2

x − 2 y + 3

z −1

3

−1

2

= 0 7x–17y–19z–46=0.

4

5

− 3

Ответ: 7x–17y–19z–46=0.

№11. Написать каноническое уравнение прямой, проходящей через точку М0(5,–3, 2 ) и параллельной вектору, образующему с координатными ортами

углы α = π3 , β = π3 , γ = π4 . Лежат ли на этой прямой точки P(1,–2,3), Q(4,–4,0)?

№12. Составить уравнение плоскости, проведенной через точку M0 (x0 ; y0 ; z0 ) перпендикулярно двум пересекающимся плоскостям A1x + B1 y +C1z + D1 = 0 и A2 x + B2 y + C2 z + D2 = 0. Написать уравнение для случая, когда M0 (2;−3;1) и плоскости заданы уравнениями 3x − y + 2z −1 = 0 , 4x +5y −3z + 2 = 0 .

32

Решение:

n1 (A1 , B1 ,C1 ) и n2 (A2 , B2 ,C2 ) – векторы нормалей к соответствующим плоскостям. Задача сводится к составлению уравнения плоскости, проходящей через данную точку M0 параллельно двум неколлинеарным векторам. Векторы

,

,

компланарны,

где M(x, y, z) –

произвольная

точка искомой

M0 M

n1

n2

плоскости.

x − x0

y − y0

z − z0

A1

B1

C1

= 0 – уравнение искомой плоскости.

A2

B2

C2

Для конкретного случая получаем

x − 2

y + 3

z −1

3

−1

2

= 0 7x −17y −19z − 46 = 0 .

4

5

−3

Ответ: 7x −17y −19z − 46 = 0.

№13. Вычислить расстояние

между двумя

прямыми в

пространстве:

L1 : x = 3 + 2t , y = 7 − 2t , z =1+3t , t R , L2 : x = 5 + 4t , y = 8 , z = 2 − 6t , t R .

Решение:

M1 (3,7,1), M2 (5,8,2), M1M2 (2,1,1). a1 (2,−2,3), a 2 (4,0,6).

	2	1	1		1	1	1
=	2	− 2	3	= 4	1	− 2	3	= 56 ≠ 0 L1 и L2 – скрещивающиеся
	4	0	− 6		1	0	−3

прямые.								56					56		56
d = [				]=								− 2 2 =		=		=
		,				3 2			3 2				144 + 576 + 64		784
	a1		a2		− 2		+	2		+	2
					0	− 6		4	− 6		4	0
= 56 = 2 .
28
Ответ: d = 2 .
№14. Составить						уравнение			плоскости,			проходящей через точку P(4;−1;1) и

2x −3y + 5z −7 = 0 прямую L : 4x + 2y −6z −5 = 0 .

Решение:

Уравнение пучка плоскостей, проходящих через прямую L:

(2x −3y +5z −7)+ λ(4x + 2y −6z −5)= 0 , λ = αβ , α ≠ 0 .

33