Тема 1

Тема 1. ВВЕДЕНИЕ В ЧИСЛЕННЫЕ МЕТОДЫ

Современная технология исследования сложных научно-технических проблем, в том числе связного характера, основана на построении и анализе с помощью ЭВМ математических моделей изучаемого объекта (устройства, системы, сети связи). Такой метод исследования называется вычислительным экспериментом (ВЭ). Специалисту по телекоммуникациям для успешного применения последнего в практической деятельности необходимо овладеть знаниями в дисциплинах, непосредственно связанных с использованием вычислительной техники. Основной такой дисциплиной является вычислительная математики (прикладная математика), которая изучает способы построения и исследования численных методов решения математических задач, моделирующих различные процессы. Численные методы разрабатываются и исследуются высококвалифицированными специалистами в области прикладной математики, главной задачей студентов, в будущем инженеров по телекоммуникациям, является понимание основных идей методов, особенностей и областей их применения.

Схема ВЭ [1] состоит из пяти основных этапов (рисунок 1): постановки задачи (ПЗ), построения математической модели (ММ), применения численного метода решения (ЧМР), программирования (П), проведения вычислений и анализа результатов (ПВиАР).

На этапе ПЗ формулируется цель исследования и описание проблемы в виде основных законов, управляющих объектом исследования. Эти основные законы представляют собой физическую модель (ФМ) процесса, в которой некоторые физические факторы учтены, а некоторыми можно пренебречь. На втором этапе ФМ ставится в соответствие математическая модель (ММ), представляющая собой математическое описание физического процесса в виде алгебраических, дифференциальных, интегральных и других уравнений, которые, как правило, выражают законы сохранения основных физических величин. Большинство реальных процессов описывается нелинейными уравнениями и лишь в первом приближении (при малых значениях параметров, малых отклонениях и т.д.) эти уравнения можно заменить линейными. Основные требования к ММ следующие:

1.Адекватность рассматриваемому явлению – в рамках допустимой погрешности ММ точно отражает характерные черты данного явления;

2.Сравнительная простота;

3.Доступность исследования.

Методами классической математики полученную ММ исследуют и получают ответы на вопросы: правильно ли поставлена задача, хватает ли исходных данных, не противоречат ли исходные данные друг другу, существует и единственно ли решение поставленной задачи. Также оценивают область применения выбранной ММ.

ПЗ ФМ

ММММ

ЧМР	ДМ → ВА

П

ПВ и АР

Рисунок 1 – Схема вычислительного эксперимента

Для поиска решения задачи, представленной в виде ММ, применимы методы из различных групп. К точным аналитическим методам относятся методы, в которых решение задачи удается выразить в виде аналитических выражений из набора элементарных функций или в виде конечного вычислительного алгоритма (ВА) – конечного числа строгой последовательности арифметических и логических действий (решение считают точным, если нет ошибок округления). К приближенным аналитическим методам относятся методы, в которых за счет некоторых допущений исходную задачу сводят к эквивалентной задаче, имеющей точное аналитическое решение. Как правило, лишь для ограниченного круга задач можно применить методы, принадлежащие указанным двум группам, в общем случае решение задачи осуществляют с помощью численных методов.

На третьем этапе ВЭ производят построение приближенного численного метода решения задачи путем преобразования ММ в дискретную модель (ДМ), пригодную для реализации на ЭВМ. На основе последней осуществляют выбор ВА – конечной последовательности арифметических и логических действий, обеспечивающих получение решения задачи с заданной контролируемой погрешностью. Поскольку разработкой численных методов занимаются высококвалифицированные специалисты в области прикладной математики, инженеру-связисту необходимо из имеющегося набора широко известных методов выбрать тот, который наиболее приемлем в каждом конкретном случае.

На четвертом этапе осуществляют реализацию ВА в виде программы на ЭВМ в одной из сред программирования или используют любой из современных математических пакетов прикладных программ – систем компьютер-

ной математики (MathCAD, MATLAB, Mathematica, Deriv, Maple и др.), в ко-

торых многие широко известные численные методы решения задач реализованы в виде встроенных функций, а иногда и пакетов-расширений [2-7]. Составленная программа подлежит отладке – контролю и диагностике ошибок, исправлению ошибок, решению контрольных (тестовых) задач для получения уверенности в достоверности результата.

На последнем этапе проводят решение поставленной задачи на ЭВМ и выполняют анализ полученных численных результатов. На основе результатов анализа осуществляют уточнение ММ, если последняя оказалась слишком грубой и результат вычислений не согласуется с физическим экспериментом или слишком сложной и решение с достаточной точностью можно получить при более простых моделях. В этом случае происходит не только уточнение ММ, но и уточнение ЧМР и программы на ЭВМ, поэтому считается, что ВЭ есть расчет серий вариантов решений поставленной задачи для различных математических моделей. Основу ВЭ составляет триада: модель – метод (алгоритм) – программа.

Именно ЧМР (ВА) задач прикладной математики, а именно: широко известные методы решения систем линейных алгебраических уравнений, нелинейных алгебраических уравнений и их систем, различных дифференциальных уравнений и их систем, а также сопутствующие вопросы приближения функций, дифференцирования и интегрирования функций – являются предметом изучения в дисциплине «Численные методы анализа». Такие этапы ВЭ как постановка задачи, построение ММ, программирование, организация вычислений и интерпретация результатов в явном виде в рамки указанной дисциплины не входят.

При применении такого метода исследования технической проблемы как ВЭ неизбежно получают не точное, а приближенное решение исходной задачи. Общая погрешность результата «складывается» из погрешностей различных типов. В соответствии со схемой ВЭ погрешности делятся на три группы: неустранимая погрешность, погрешность численного метода и вычислительная погрешность.

Неустранимая погрешность обусловлена неточным математическим описанием задачи. Во-первых, входные данные (начальные и граничные условия, коэффициенты и правые части уравнений ММ), полученные, как правило, экспериментально, всегда задаются с некоторой погрешностью. Вовторых, любая ММ является определенной идеализацией рассматриваемого физического явления и описывает лишь основные факторы, существенные при решении конкретной технической задачи. Этот факт указывает на погрешность, возникающую вследствие несоответствия математического описания реальности. Неустранимая погрешность не контролируется в процессе численного решения и может быть уменьшена только за счет более точного описания физического явления и более точного определения параметров ММ.

Погрешность численного метода возникает при замене ММ исходной задачи ее дискретным эквивалентом, на основе которого строится ВА. Поскольку при построении ВА точное решение представляется в виде бесконечного предела последовательности арифметических и логических действий, то при ограничении числа вычислений вносится погрешность, контролируемая некоторыми параметрами метода. Одной из основных задач вычислительной математики является получение зависимости погрешности решения от параметров численного метода. Эту зависимость называют асимптотической оценкой погрешности ВА, выражение которой не всегда просто найти. Если при уменьшении некоторого параметра метода h ( h →0 ) по-

грешность решения εh →0 и выполняется условие εh <C h p , где C = const не зависит от h , то считают, что порядок погрешности метода равен p и обозначают коротко εh ≈O(h p ).

Вычислительная погрешность возникает вследствие округления чисел при проведении вычислений. Одним из источников вычислительной погрешности является приближенное представление вещественных чисел в ЭВМ, обусловленное конечностью разрядной сетки. Кроме того, величина вычислительной погрешности зависит от чувствительности алгоритма к погрешностям округления, поскольку ошибки округления в процессе счета могут накапливаться, а могут и компенсироваться. В устойчивых алгоритмах в про-

цессе вычислений погрешности округления возрастают незначительно, а в неустойчивых алгоритмах накопление погрешностей округления может привести к переполнению арифметического устройства ЭВМ. Поэтому второй важной задачей вычислительной математики является установление условий устойчивости ВА и разработка рекомендаций по созданию устойчивых методов.

Введем формальные определения: a – точное значение отыскиваемого параметра; a~ – значение этого параметра, соответствующее принятому ма-

~

тематическому описанию; ah – значение этого параметра, полученное при

~

реализации численного метода в предположении отсутствия округления; ah

– приближенное значение отыскиваемого параметра, полученное при реальных вычислениях (с учетом округления). Тогда неустранимая погрешность ρ1 = a~ − a , погрешность метода ρ2 = a~h − a~ , вычислительная погрешность

~	~	~	− a =ρ1 + ρ2 + ρ3 . Од-
ρ3 = ah	− ah	определяют полную погрешность ρ0 = ah

нако, под погрешностью понимают не просто разницу между приближениями, а некоторую меру близости – расстояние между объектами. Например, в скалярном случае – это расстояние между точками на числовой оси, т.е.

ρ0

=

~

− a

ah

ρ1

=

~

a − a

ρ0 ≤ρ1 + ρ2 + ρ3

(1.1)

ρ2

=

~

~

ah

− a

ρ3

~

~

= ah

− ah

Для оценки близости между объектами – функциями ( f (x) и g(x)), векторами ( xr и yr), матрицами ( A и B ) – учитывают то обстоятельство, элементами какого нормированного пространства эти объекты являются [8].

Нормированное пространство – это такое множество элементов (функций, векторов, матриц), в котором каждому элементу Χ из этого пространства поставлено в соответствие число Χ (называется нормой), удовлетворяющее условиям:

1.Χ ≥ 0 , причем Χ = 0 при Χ = 0

2.αΧ = α Χ , причем α может быть комплексным числом

3.Χ1 + Χ2 ≤ Χ1 + Χ2 , т.е. выполняется неравенство треугольника.

Близость (расстояние) между элементами нормированного пространства определяется через норму

ρ(Χ1, Χ2)=				Χ1 − Χ2				.	(1.2)

Определение нормы зависит от вида используемого нормированного пространства и класса рассматриваемых объектов (функций, векторов, матриц).

В качестве примера рассмотрим нормированное пространство C[a,b], состоящее из множества непрерывных функций {f (x), g(x),h(x),K}, определенных на интервале [a,b], в котором норма функции f (x) и расстояние между функциями f (x) и g(x) вычисляются по следующим выражениям [8]:

f

C

= max

f (x)

,

x [a,b]

(1.3)

ρ

C

(f , g)= max

f (x)− g(x)

.

x [a,b]

В противовес указанному есть нормированное пространство L2 [a,b], состоящее из множества кусочно-непрерывных функций на интервале [a,b], интег-

рируемых на этом интервале с квадратом (т.е. ∫b f (x)2 dx < ∞), в котором

a

норма функции f (x) и расстояние между функциями f (x) и g(x) представляются в отличие от (1.3) другими зависимостями [8]:

b

f

L2 = ∫ f (x)2 dx,

a

(1.4)

b

ρL2 (f , g)= ∫ f (x)− g(x)2 dx.

a

В пространстве L2 [a,b] вводят понятие скалярного произведения

(f , g)L = ∫b

f (x)g(x)dx,

(1.5)

2

a

причем,

(f , f )L

=

f

2 , а для ортогональных функций

f (x)

и g(x) –

2

L

(f , g)L

2

= 0 .

2

По аналогии с нормированными пространствами C[a,b] и L2

[a,b] мож-

но ввести понятие норм и расстояний для векторов и матриц [8]. Например, в

множестве векторов {x, y,K}, где x = (x1, x2 ,K, xn ),

y =(y1, y2 ,K, yn )

xr

C

= max

xi

,

xr − yr

C

= max

xi − yi

,

(1.6)

i

i

xr L

n

xr − yr L

n

− yi )2

= ∑xi2 ,

=

∑(xi

,

(1.7)

2

i=1

2

i=1

, B = (bij )i, j=

а в множестве матриц {A, B,K}, где A = (aij )i, j=

1,n

1,n

n

n

A

C

= max ∑

aij

,

A − B

C

= max ∑

aij

−bij

,

(1.8)

i

j=1

i

j=1

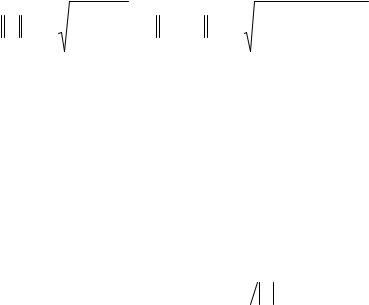
	n n		n n	(aij −bij )2 .
A L =	∑∑aij2 ,	A − B L =	∑∑		(1.9)
2	i=1 j=1	2	i=1 j=1

Какие бы объекты (функции, векторы, матрицы, числа) не рассматривались, при определении погрешности решения задачи используют понятия

абсолютной и относительной погрешности. Если~Χ точное значение некото-

рого элемента нормированного пространства, а Χ его приближенное значе~-

ние, то абсолютная погрешность

Χ определяется нормой разности Χ и Χ

(в скалярном случае x =

~

)

x − x

ΔΧ =

~

,

(1.10)

Χ − Χ

а относительная погрешность отношением абсолютной погрешности к норме

элемента (в скалярном случае δx =					~
					x x )
	ΔΧ
δΧ =		~		.	(1.11)
		Χ

Для получения достоверного результата при применении численного метода решения конкретной технической задачи исследователю необходимо следить за точностью. Целенаправленно повышать точность при заданных входных данных и выбранной ММ можно путем уменьшения погрешности метода или вычислительной погрешности. Оценкой погрешности при округлении чисел, выполнении вычислительных операций над числами занимается теория погрешностей.

ЭВМ обрабатывает числа, представленные в позиционной системе счисления – с фиксированной точкой или с плавающей точкой [9]. Позиционное представление числа по основанию r определяется правилом

±

(Ka a a

0

.a

−1

a

−2

K)

= ±(K+ a

r 2 + a r + a

0

+ a

−1

r −1

+ a

−2

r −2

+K), (1.12)

2 1

r

2

1

где r

– целое число большее единицы;

ai

– цифры представления, 0 ≤ ai < r .

Данное правило соответствует представлению числа в форме с фиксированной точкой. Однако наиболее приемлема [9] для проведения арифметических операций запись числа в форме с плавающей точкой – в виде

N = ±M r p ,

(1.13)

где r – основание системы счисления; p – порядок числа (любое целое);

M – дробная часть числа (иногда называется мантиссой), записанная в форме числа с фиксированной точкой ( 0.d1d2d3 Kdk ). Условие нормировки

r −1 ≤		M		<1,	(1.14)

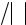
обеспечивающее единственность представления любого числа в форме с плавающей точкой, указывает на нормализованную форму записи чисел, с которой работает большинство ныне применяемых стандартных подпрограмм.

Итак, любое число N в системе счисления по основанию r соответствует записи N = ±0.d1d2 Kdk r p , из которой следует, что подмножество действительных чисел, с которым оперирует конкретная ЭВМ, конечно, опреде-

ляется разрядностью			k	и границами порядка p ( p1 ≤ p ≤ p2 )	и содержит
2(r −1)(p	2	− p +1)r k−1	+1	чисел. Причем, границы порядка p	и p	2	задают
		1		1
ограниченность действительных чисел по величине, а размерность k							– дис-

кретность распределения их на отрезке числовой оси. Разность между двумя соседними значениями равна единице последнего разряда. Число меньшее этой разности соответствует машинному нулю ( N0 ).

Таким образом, ЭВМ оперирует приближенными значениями действительных чисел, мерой точности которых является погрешность. Как правило, истинное значение числа x неизвестно, имеется его приближенное значение

x , поэтому речь ведут о предельной абсолютной и относительной погрешно-
~		x	яв-
стях приближенного числа x . Предельная абсолютная погрешность
~		~	x .
ляется верхней оценкой абсолютной погрешности x числа x , т.е. x ≤
			~
~	~ ~	+	~
В этом случае истинное значение x находится в интервале (x −	x, x		x ).

Для приближенного числа, полученного в результате округления (правило округления для десятичной системы счисления [9, 11]: если старший отбрасываемый разряд меньше пяти, то предшествующая ему цифра в числе не меняется; если старший отбрасываемый разряд больше пяти, то предшествующая ему цифра увеличивается на единицу; при старшем отбрасываемом разряде равном пяти по общепринятому соглашению округления до четного, позволяющему устранить некоторые особые случаи при операциях над числами с плавающей точкой, предшествующая четная цифра не меняется, я нечетная увеличивается на единицу) предельная абсолютная погрешность ~x принимается равной половине единицы последнего разряда числа. Например,

x =151.77	,	x = 0.005 (т.е.	x ≤ 0.005); x =14.0 ,	x = 0.05 (т.е. x ≤ 0.05).
~		~	~	~

Предельное значение относительной погрешности есть отношение пре-

дельной абсолютной погрешности					x к абсолютной величине приближенно-
					~
го числа	~	~	~	~	~
	x , т.е.	δx =	x	x . Информацию о том, что x является приближен-
ным значением числа					~
			x с относительной погрешностью δx , записывают в
~	~	~		~
виде x(1	− δx )≤ x ≤ x(1		+ δx ).

При переходе от одной формы записи приближенного числа к другой придерживаются правила, что пределы изменения, указываемые новой формой записи, шире старых, т.е. при переходе от выражений при абсолютной

погрешности			к	выражениям при относительной	~	(1	~		~	−	~
					x		− δx )≤ x				x ,
~	~	~	~
x(1 + δx )≥ x +			x и, наоборот, при переходе от выражения через относитель-
ную	погрешность			к выражению через абсолютную	~	−	~	~	(1		~
					x		x	≤ x		− δx ),
x + x ≥ x(1 + δx ).
~	~	~	~

Приведенные оценки погрешностей приближенных чисел справедливы, если в записи этих чисел все значащие цифры верные. Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева (например, ~x = 0.03045 , ~x = 0.0304500 ). Значащую цифру называют верной, если абсолютная погрешность числа не превосходит половины единицы раз-

ряда, соответствующего этой цифре (например,		~	= 0.03045 и x = 0.000003;
		x
~	= 0.0304500 и x = 0.0000007 ). Цифры не являющиеся верными называют
x

сомнительными. Если все значащие цифры верные, то число записано со всеми верными цифрами. Приближенное число принято записывать таким образом, чтобы вид записи давал информацию о его абсолютной погрешности, которая не должна превосходить единицы последнего разряда, сохраняемого при записи. Поэтому записывают только верные цифры, не отбрасывая верные нули на конце числа (т.е. запись числа ~x =14.0 указывает на погрешность, которая должна быть меньше 0.05 ).

При изменении формы записи числа – с фиксированной или с плавающей точкой – также соблюдают равносильность преобразований: число значащих цифр в числе не должно меняться.

Итак, относительная точность представления приближенных чисел в ЭВМ определяется принятым правилом округления. В системе с однократной точностью вычислений [9], когда округление соответствует отбрасыванию всех разрядов дробной части, выходящих за пределы разрядной сетки, отно-

сительная точность представления числа

ε

≤ r

1−k

~

= x(1 +

ε

),

~

≥ N0 )

(т.е. x

x

имеет специальное название – один ulp (Unit in the Last Place), что означает одну единицу в последнем разряде дробной части. В системах с многократной точностью [9] используются более точные способы округления, благодаря чему предельное значение относительной погрешности (машинного эпси-

лона) улучшают до ε ≤ 0.5r1−k .

Несмотря на достаточно высокую точность представления чисел в ЭВМ, при проведении вычислений погрешность может накапливаться. Выполнение любой арифметической операции вносит некоторую погрешность. Для определения величины этой погрешности воспользуемся прямой задачей теории погрешности [10, 11]. В области G n -мерного числового пространства рассматривается непрерывно дифференцируемая функция

y = f (a1,a2 ,K,an ). В некоторой точке (a1,K,an ) области G нужно вычислить значение функции y , однако известны лишь приближенные значения аргу-

~	~	~	~	~	~
ментов a1 , a2 , …,		an	такие, что точка (a1	,a2	,K,an ) G . Известны погрешно-
					~	~	~	~
сти этих приближенных значений аргументов – a1 ,						a2 , …,	an или	δa1 ,
~	~							~
δa2 , …,	δan . Требуется вычислить приближенное значение функции							y и

оценить его отклонение от точного значения y (т.е. рассчитать абсолютную ~y и относительную δ~y погрешности). Так как функция непрерывно дифференцируема, то она ограничена. Для определения погрешностей используют формулу конечных приращений Лагранжа [8, 11], согласно которой

~		~	n		~	~		~
	=				∂f (a1	,K,an )			(1.15)
y		y − y	≤ ∑		∂ai			ai .
			i=1

Абсолютная погрешность дифференцируемой функции одного										аргумента
y = f (a), вызываемая достаточно малой погрешностью аргумента										~
										a , опре-
деляется величиной
~		~		≤		f	′ ~		~	(1.16)
y =	y − y						(a )		a .
В соответствии с (1.11) значение относительной погрешности
~	~
	y	~ .								(1.17)
δy ≤
		y

Поскольку арифметические операции являются простейшими функциями двух аргументов, для определения погрешности, вносимой проведением этих операций над приближенными числами, воспользуемся указанным общим подходом.

При суммировании

(вычитании)

двух

чисел y = f (a1,a2 )= a1 ± a2

( ai > 0 ), поскольку

~

~

=1, то

∂f (a1

,a2 )

∂ai

~

2

~

(1.18)

y

= ∑

ai .

i=1

~

~

~

~

2

~

~

~

= ∑

ai

В соответствии с (1.17) δy

=

y

y

ai

a1

± a2

, поэтому

~

~

i=1

ai

2

~

= ∑

ai

~

δy

δai .

(1.19)

~

~

i=1

a1

± a2

Анализ (1.18) и (1.19) показывает, что абсолютная погрешность суммы не может быть меньше абсолютной погрешности наименее точного из слагае-

мых. Если обозначить	~	~
	m = min δai ,	M = max δai , то в случае суммирования
	i	i

относительная погрешность результата заключена между наименьшим и