§4. Задача нахождения кратчайшего пути на сети.
Постановка задачи. Задана конечная ориентированная сеть , где I - множество вершин, U - множество дуг. В сети S зафиксированы две вершины s и t. Каждая дуга имеет вес , который обозначает расстояние от вершины i до вершины j. Требуется на заданной сети найти путь из вершины s в вершину t наименьшей длины.
Напомним, что путем из вершины s в произвольную вершину j называется цепь, соединяющая эти две вершины, причем первая дуга имеет начало в вершине s, а для каждой последующей дуги ее начало совпадает с концом предыдущей. Говорят, что все дуги пути при движении от вершины s до вершины j являются прямыми. Под длиной пути понимают суммарный вес его дуг.
Решение задачи. Все необходимые обозначения даны в постановке задачи. Задачу решим методом динамического программирования. Первый этап метода – погружение задачи в семейство аналогичных задач. Будем считать, что требуется найти кратчайший путь из вершины s в произвольную вершину j.
Введем функцию Беллмана – значение длины минимального пути из вершины s в вершину j . Понятно, что при j = t получим исходную задачу.
Перейдем ко второму этапу метода динамического программирования – составлению уравнения Беллмана. Рассмотрим вершину j и для нее определим множество вершин соседних «слева»:
= ,
т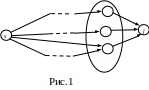
.е.
во множество попадут
те вершины, из
которых непосредственно можно попасть
в вершину j
(см. рис.1).
Используя
принцип оптимальности, будем считать,
что до каждой из вершин путь найден
оптимальный. Согласно введенным
обозначениям он равен .
Очевидно, что путь из вершины s
в вершину j
через каждую из вершин равен
, . (4.1)
Для определения кратчайшего пути из вершины s в вершину j надо найти минимальное значение среди значений (4.1). Таким образом, мы получаем уравнение Беллмана:
= min ;\s\do9(i(I\o( j;\d\fo3(ˉ , . (4.2)
Начальное условие для этого уравнения очевидно
= 0. (4.3)
Третий этап метода динамического программирования – поиск решение уравнения (4.2) с начальными условиями (4.3) и построение по нему решения исходной задачи.
Обозначим через множество вершин, для которых значение функции Беллмана известно. Отметим, во-первых, что это множество не пусто, поскольку согласно (4.3) , а во-вторых, если , то задача решена, и – значение кратчайшего пути из вершины s в вершину t.
Рассмотрим случай, когда . Построим на сети S разрез
= .
Пусть . Рассмотрим любую вершину k \ и всевозможные пути из вершины s в вершину k. Очевидно, что любой такой путь содержит хотя бы одну дугу разреза, а это в свою очередь означает, что справедливо неравенство
min ;\s\do9((i . (4.4)
Обозначим дугу, на которой достигается минимум в правой части неравенства (4.4), как , :
min ;\s\do9((i =
Ясно, что неравенство (4.4) при превращается в равенство
= ,
что означает: вершину следует добавить к множеству .
Продолжим аналогичные рассуждения для нового множества . Через конечное число шагов (в силу конечности сети) либо найдем значение , либо для вновь построенного множества разрез . В первом случае решение уравнения завершено, т.к. найдено искомое значение кратчайшего пути из вершины s в вершину t, во втором случае решение прекращается, т.к. в сети не существует пути из вершины s в вершину t.
Алгоритм решения. Для реализации указанной выше схемы решения задачи служит так называемый алгоритм пометок. Каждая вершина i сети сначала получает временную метку, состоящую из двух частей. Первая часть метки дает некоторое значение пути из вершины s в вершину i, вторая часть метки – это номер вершины, по которой определилась первая часть метки. В ходе алгоритма некоторые временные метки становятся постоянными, и тогда первая часть метки дает наименьшее значение пути из вершины s в вершину i .
Шаг предварительный. 1) Вершина s получает метку [0; ], причем эта метка считается постоянной. 2) Формируем множество вершин, имеющих постоянную метку: = {s}.
Шаг основной. 1) Для множества формируем множество вершин, соседних «справа»
.
2) Если , то решение прекращается: в сети нет пути из вершины s в вершину t.
3) Если , то для каждой вершины j вычисляем первую часть временной метки по формуле:
= min ;\s\do10(i(I\s\up2( * ; (4.5)
вторая часть метки – это номер вершины из множества , на которой определился минимум в (4.5).
4) Среди всех вершин с временными метками находим вершину , у которой первая часть метки минимальна:
= min ;\s\do10(j(((I\s\up2( * ;
Метка этой вершины становиться постоянной, к множеству добавляем вершину .
5) Если t, то переход к пункту 1) основного шага.
6) Если = t, то = – искомое значение кратчайшего пути из вершины s в вершину t.
7
)
Восстанавливаем вершины, через которые
проходит путь, используя вторые части
меток. Начинаем с вершины t,
номер во второй части ее метки показывает
предыдущую вершину пути, номер во второй
части метки вершины показывает
предшествующую ей вершину и т.д. пока
номер во второй части метки не совпадет
с s.
Пример. Пусть имеется сеть , изображенная на рис. 2, здесь указаны веса дуг . Требуется на заданной сети найти кратчайший путь из вершины 1 в вершину 8.
Применим алгоритм пометок.
Итерация 1.
Вершина 1 получает постоянную метку [0; ]. = {1} – множество вершин, имеющих постоянную метку.
2) Формируем множество вершин, соседних «справа»
.
3) Вычисляем согласно (4) первую часть временной метки для каждой вершины из :
= min ;\s\do10(i(I\s\up2( * = 0 + 2 = 2;
= min ;\s\do10(i(I\s\up2( * = 0 + 7 = 7;
= min ;\s\do10(i(I\s\up2( * = 0 + 10 = 10.
Вторая часть метки у всех вершин одинаковая. Итак,
2: [2; 1], 3: [7; 1], 4: [10; 1].
4) Среди вершин с временными метками находим вершину , у которой первая часть метки минимальна: . Остальные метки «забываем».
5) = {1, 2} – новое множество вершин, имеющих постоянную метку. Переход к следующей итерации.
Итерация 2.
Информация о второй итерации записана в табл. 4.1.
Таблица 4.1.
|
|
Вычисление первой части метки |
Метка |
{1, 2} |
3 |
min ;\s\do10(i(I\s\up2( * = 0 + 7 = 7 |
[7; 1] |
|
4 |
min ;\s\do10(i(I\s\up2( *=min = 7 |
[7; 2] |
|
5 |
min ;\s\do10(i(I\s\up2( * = 2 + 6 = 8 |
[8; 2] |
Среди вершин с временными метками находим вершину , у которой первая часть метки минимальна. В данном случае таких вершин две: 3 и 4, обе вершины добавляем к множеству .
= {1, 2, 3, 4} – новое множество вершин, имеющих постоянную метку.
Переход к следующей итерации.
Итерация 3.
Информация о третьей итерации записана в табл. 4.2.
Имеем – вершина с минимальной временной меткой. Добавляем ее к множеству .
Итерация 4. (См. табл. 4.3.).
Имеем – вершина с минимальной временной меткой. Добавляем ее к множеству .
Таблица 4.2.
|
|
Вычисление первой части метки |
Метка |
{1,2,3,4} |
5 |
min ;\s\do10(i(I\s\up2( * = min = 8 |
[8; 2] |
|
6 |
min ;\s\do10(i(I\s\up2( *=min = 11 |
[11; 4] |
Табл. 4.3.
|
|
Вычисление первой части метки |
Метка |
{1,2,3,4,5} |
6 |
min ;\s\do10(i(I\s\up2( *=min = 11 |
[11; 4] |
|
7 |
min ;\s\do10(i(I\s\up2( * = min = 15 |
[15; 4] |
|
8 |
min ;\s\do10(i(I\s\up2( *=min = 17 |
[17; 5] |
Итерация 5. (См. табл. 4.4.).
Табл. 4.4.
|
|
Вычисление первой части метки |
Метка |
{1, 2, 3, 4, 5, 6} |
7 |
min ;\s\do10(i(I\s\up2( *=min = =13 |
[13; 6] |
|
8 |
min ;\s\do10(i(I\s\up2( *=min = 17 |
[17; 5] |
Имеем – вершина с минимальной временной меткой. Добавляем ее к множеству .
Итерация 6. (См. табл. 4.5.).
Табл. 4.5.
|
|
Вычисление первой части метки |
Метка |
{1, 2, 3, 4, 5, 6, 7} |
8 |
min ;\s\do10(i(I\s\up2( * = min = = 15 |
[15; 7] |
Имеем – вершина с минимальной временной меткой. Метка вершины 8 становится постоянной, а значит, 15 – искомое значение кратчайшего пути из вершины 1 в вершину 8. По второй части меток восстанавливаем вершины, через которые кратчайший путь проходит:
8 7 6 4 2 1.
На рис. 3 искомый путь выделен.
