SlPr

4.4.Порядок выполнения работы

4.4.1.Рассчитать матрицы вероятностей перехода, векторы безусловных вероятностей и среднее состояние цепи Маркова для последовательности шагов 1Kn . Вариант описания цепи Маркова взять из таблицы 3.1.

4.4.2.Построить графики изменения вероятностей первой строки матрицы вероятностей перехода, безусловных вероятностей и среднего состояния, рассчитанных в п. 4.4.1.

4.4.3.Оформить полученные результаты в виде отчета.

21

Тема 5. Предельные вероятности состояний цепей Маркова.

5.1.Цель работы

5.1.1.Приобретение навыков расчета предельных вероятностей цепей Маркова

5.2.Теоретические положения

Часто нас интересует поведение системы, описываемой цепью Маркова, на достаточно длительном промежутке времени. Это значит, что нас интересует поведение вероятностей

перехода цепи Маркова за n шагов pi, j (n) при n → ∞ . В некоторых случаях эти вероят-

ности сходятся при n → ∞ к некоторым предельным значениям, которые называются пре- дельными вероятностями. Условия существования предельных вероятностей определяет следующая теорема.

Терема (Маркова). Если существует такое s > 0, что все pi, j (s) > 0, то существуют та-

кие числа p j , j =1,2,...,k , что независимо от индекса i выполняются следующие соотно- шения:

lim pi, j (n) = p j , j =1,2,...,k ,		(5.1)
n→∞
k
å p j	=1.

j =1

Физический смысл этой теоремы состоит в том, что вероятности pi, j (n) перехода из со- стояния Ei в состояние E j за n шагов при n → ∞ не зависят от состояния Ei , из которого

был начат переход. Система как бы забывает о своем состоянии в далеком прошлом. Пример. Применима ли теорема о предельных вероятностях к цепи Маркова с матрицей

вероятностей перехода	0	1
æ			ö
P = ç			÷?
ç	1	0	÷
è			ø

Поскольку для такой цепи		1	0				0	1
P	æ			ö		æ			ö
	= ç			÷ , P		= ç			÷, m = 1,2,... ,
2m	ç	0	1	÷	2m+1	ç	1	0	÷
	è			ø		è			ø

то для каждого s матрица Ps имеет нулевые элементы. Условия теоремы не выполняются, так что мы не можем утверждать, что предельные вероятности существуют.

Объединим предельные вероятности p j , j =1,2,...,k , в вектор-строку предельных веро-

ятностей
( p )T = ( p , p ,..., p ) .			(5.2)
1	2	k
Тогда выражение (5.1) можно записать в следующей векторно-матричной форме:
lim P = P		,	(5.3)
n→∞	n

где P – (k × k)-матрица предельных вероятностей. Все строки матрицы P одинаковы и совпадают с вектором-строкой ( p )T (5.2).

22

Теорема. Если для цепи Маркова существует вектор-столбец предельных вероятностей p (5.2), то он удовлетворяет следующей системе линейных алгебраических уравнений:

	PT p = p ,		(5.4)
	k
	å p j =1.		(5.5)
	j =1
Действительно, запишем для цепи Маркова уравнение Чэпмена–Колмгорова (4.2) в виде
	Pn+1 = Pn P	= Π , P = Π
и найдем предел обеих частей при n → ∞ . Поскольку при этом P			, то по-
лучаем уравнение	n+1	n
	P = P P ,
из которого следует (5.4).
Рассмотрим также безусловные предельные вероятности
a j	= lim a j (n) ,
	n→∞

образующие вектор-строку безусловных предельных вероятностей (A )T = (a ,a ,...,a ) ,
так что		1 2	k
(A )T = lim A .			(5.6)
n→∞	n	P (5.2), то он является и
Теорема. Если существует вектор предельных вероятностей
вектором безусловных предельных вероятностей:
A = P .			(5.7)

Чтобы получить равенство (5.7), запишем соотношение (4.5), взяв предел от обеих его

частей:				lim AT	= AT
						lim P .
			n→∞ n		0	n→∞	n
Учитывая обозначения пределов (5.3), (5.6), получим
				(A )T = AT Π .
						0
Поскольку a (0) + a	2	(0) + ... + a	k	(0) = 1	и матрица P состоит из одинаковых строк, то
1

легко понять, что A0T Π = (P )T , и равенство (5.7) доказано.

Пример 5.4. Найти предельные вероятности для цепи Маркова из примера 5.1 раздела 5.1 (см. п. 3.2) на урновую модель.

Поскольку матрица вероятностей перехода этой цепи (3.2) имеет вид

					æ		1	2		ö
æ	p	p	ö		ç					÷
							3	3
ç	1,1	1,2	÷		ç					÷
P = ç p2,1		p2,2	÷	=	ç		1		5	÷	,
è			ø		ç			6		÷
					è 6					ø

т.е. не содержит нулевых элементов, то эта цепь удовлетворяет теореме 5? и предельные ве- роятности существуют.

Система уравнений (5.4), (5.5) для предельных условных вероятностей в данном примере

имеет вид

23

13 p1 + 16 p2 = p1 , 23 p1 + 56 p2 = p2 ,

p1 + p2 =1.

Поскольку первые два уравнения являются линейно зависимыми, то, отбрасывая первое из них, получим два уравнения с двумя неизвестными

23 p1 − 16 p2 = 0, p1 + p2 =1.

Отсюда получаем p1 = 0,2, p2 = 0,8. Такими же будут и безусловные предельные вероят-

ности a1 = 0,2 , a2 = 0,8 . Это значит, что после продолжительного числа экспериментов мы будем на каждом шаге вынимать белый шар с вероятностью a1 = 0,2 и черный шар – с вероятностью a2 = 0,8 .

5.3. Программные средства для выполнения работы

Для выполнения задания необходимо уметь решать систему линейных алгебраических уравнений, т.е. систему вида

ax = b ,

где a = (ai, j ) , i, j =1,n , – квадратная матрица коэффициентов системы, b = (bi ), i =1,n, –

вектор-столбец свободных членов, x = (xi ) , i =1,n, – вектор-столбец неизвестных. В Mat-

lab это можно сделать как методом обращения матрицы коэффициентов, т.е. с помощью ко- манды x=a^-1*b, так и методом исключения Гаусса, т.е. с помощью команды левого деления x=a\b. Метод Гаусса является более предпочтительным с точки зрения быстродействия.

5.4.Порядок выполнения работы

5.4.1.Рассчитать предельные вероятности для цепи Маркова, описание которой взять из таблицы 3.1. Убедиться в том, что полученные вероятности совпадают с вероятностями, по- лученными для той же цепи в работе 4.

24

Тема 6. Пуассоновский поток требований в СМО

6.1.Цель работы

6.1.1.Приобретение навыков моделирования реализаций Пуассоновского потока требова- ний, исследования его свойств и характеристик.

6.2.Теоретические положения

Потоком однородных событий (требований) называется конечная или счетная последова- тельность τn случайных величин, определенная на одном и том же вероятностном про- странстве, при условии, что в любой фиксированный интервал времени (a,b) с вероятно-

стью 1 попадает конечное число этих величин.

Если фиксированный момент времени t совпадает сразу с r элементами последователь- ности τn , то будем говорить, что в момент t происходит r событий потока.

Если τn ≤ τn+1 – два упорядоченных элемента последовательности, то будем говорить, что в полуинтервале [τn ,τn+1) происходит одно событие τn .

Поток требований в системе массового обслуживания (СМО) называется простейшим или Пуассоновским, если он обладает свойствами стационарности, ординарности, отсутствия последействия.

Стационарность потока означает, что для любой группы из конечного числа n непере- секающихся отрезков времени вероятность появления в них соответственно k1,k2 ,...,kn требований зависит только от этих чисел и длин указанных промежутков времени, но не за- висит от их расположения на оси времени. В частности, вероятность pk появления k требо- ваний на отрезке [T,T + t] не зависит от T и является функцией только k и t :

pk = pk (k,t) .

Ординарность потока означает практическую невозможность появления двух или более требований в один и тот же момент времени. В математической форме ординарность запи- сывается следующим образом:

	p>1(h)	→ 0,
	h
		h→0
или, иначе,
	p>1(h) = o(h) ,		(6.1)

где p>1(h) – вероятность появления на отрезке длиной h двух и более требований. Отсюда

сразу следует, что для простейшего потока

p>1(0) = 0 . (6.2)

Отсутствие последействия состоит в том, что вероятность поступления k требований в течение отрезка времени [T,T + t] не зависит от того, сколько требований и как поступали

до этого отрезка. Иначе говоря, количества требований (случайные величины), поступающие в непересекающиеся отрезки времени, независимы в совокупности.

Приведенные три свойства являются характеристическими. Другие свойства простейшего потока являются их следствием.

Прежде всего отметим, что для простейшего потока

p1(h) → λ , h h→0

25

или, иначе,
p1(h) = λh + o(h) ,	(6.3)

где λ = const . Это значит, что вероятность поступления ровно одного требования на отрез- ке времени длиной h пропорциональна длине этого отрезка. Из (6.3) следует, что

p1(0) = 0 . (6.4)

Величина λ в выражении (6.3) называется параметром простейшего потока. Физический смысл этого параметра – среднее число требований, поступающих в единицу времени. Она называется интенсивностью простейшего потока требований. Параметр λ-1 простейшего по- тока является также средней длиной отрезка времени между соседними требованиями.

Вероятность отсутствия требований на отрезке времени длиной t определяется выраже-

нием

p0 (t) = e−λt .

(6.5)

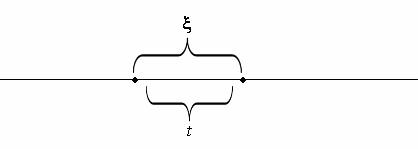
Выражение (6.5) определяет также вероятность того, что случайный отрезок времени ξ ме-

жду соседними требованиями простейшего потока будет не меньше t (см. рисунок):

P(x ³ t) = p0 (t) = e−λt .

Рис. 6.1. К закону распределения отрезка времени между соседними требованиями простей-

шего потока

Тогда

P(ξ < t) = F (t) =1 − e−λt	,	(6.6)
ξ

а это есть функция распределения случайного отрезка времени ξ между соседними требова- ниями простейшего потока. Плотность вероятности этого распределения равна

	f	ξ	(t) =	d	F (t) = λe−λt .	(6.7)
				dt
					ξ

Распределение вида (6.6), (6.7) называется экспоненциальным, т.е. отрезок времени ξ между соседними требованиями простейшего потока является случайной величиной, распределен- ной по экспоненциальному закону E(λ) (6.6).

Для вероятностей pk (t) простейшего потока справедлива система дифференциальных

уравнений

	dpk (t)	= −λpk (t)		+ λpk −1	(t) , k = 1,2,... .	(6.8)
	dt
			dp0 (t)
				= −λp0	(t) .	(6.9)
			dt

26

Как решение этих дифференциальных уравнений можно получить, что вероятность поступ- ления k требований в отрезке времени t для простейшего потока определяется выражением

pk (t) =	(λt)k	e	−λt	, k = 0,1,2,... .	(6.10)
	k!

Формула (6.10) представляет собой известное распределение Пуассона с параметром λt . Та- ким образом, число требований в отрезке времени t для простейшего потока подчиняется пуассоновскому распределению Π(λt) .

Теорема 6.1. Если τ1,τ2 ,...,τn ,... – моменты последовательных требований простейшего потока, начиная с любого момента времени t0 , то случайный вектор (τ1,τ2 ,...,τn ) имеет

плотность вероятности вида
Õn [λe−λ(ti −ti−1 ) ]= λne−λ(tn −t0 ) .	(6.11)
i =1

Последнее означает, что интервалы времени τ1 , τ2 − τ1 , …, τn − τn−1 между последова- тельными требованиями являются независимыми случайными величинами, распределенны- ми по экспоненциальному закону с параметром λ.

Теорема 6.2. При условии, что число событий простейшего потока в интервале (a,b) равно n ( ξ = n ), моменты этих событий τ1,τ2 ,...,τn независимы и равномерно распределе- ны в интервале (a,b) .

Теоремы 6.1 и 6.2 определяют два алгоритма моделирования простейшего потока требо- ваний: 1) как независимых интервалов времени между требованиями, распределенных по экспоненциальному закону (теорема 6.1); 2) как независимых моментов требований, равно-

мерно распределенных в интервале (a,b) (теорема 6.2).
Алгоритм 1.
1.	Определяем интервал (a,b) , параметр λ.
2.	Моделируем независимые последовательные интервалы времени		1 = τ1 − a ,
2 = τ2 − τ1 , …, распределенные по экспоненциальному закону с параметром			λ, до тех
	m	τ1,τ2 ,... здесь являются мо-
пор, пока τm = a + å i ≤ b , m = 1,2,... , τ0 = a . Величины
	i=1

ментами появления требований. Их число заранее не определено. Алгоритм 2.

1.Определяем интервал (a,b) , параметр λ.

2.Моделируем число требований n потока как случайное число из пуассоновского распре- деления (6.10) Π(λ(b − a)) .

3.Моделируем n независимых случайных чисел z1, z2 ,...,zn из равномерного в (a,b) распределения.

4.Сортируем случайные числа z1, z2 ,...,zn в порядке возрастания, в результате чего полу-

чаем последовательные моменты времени τ1,τ2 ,...,τn поступления требований.

5. Рассчитываем интервалы времени между требованиями 1 = τ1 − a , 2 = τ2 − τ1 , … n = τn − τn−1 .

27

6.3. Программные средства для выполнения работы

Для выполнения задания необходимо уметь моделировать случайные числа из равномер- ного, экспоненциального и пуассоновского распределений.

Случайные числа из равномерного распределения u(a,b) , плотность вероятности кото-

рого имеет вид

		ì	1
f	ξ	(x)= íï		,	a < x < b, a,bÎ R, a < b,
		ïb - a			x £ a, x ³ b,
		î	0,

моделируются с помощью функции y=unifrnd(a,b).

Случайные числа из экспоненциального распределения E(λ) , плотность вероятности ко- торого в Matlab определяется в виде

ì	−1 −λ−1
fξ (x)= íïl		e
ï		0,
î

x, x ³ 0, l > 0,

x< 0,

моделируются с помощью функции y=exprnd(lambda).

Дискретная случайная величина ξ называется распределенной по пуассоновскому закону, если она принимает значения из счетного множества {0,1,2,...,m,...} с вероятностями

P(ξ = m) = am e−a , m = 0,1,2,..., m!

где a ³ 0 – параметр распределения. Распределение Пуассона обозначается как Π(a) . Слу- чайные числа из пуассоновского распределения Π(a) моделируются с помощью функции

y=poissrnd(a).

Для графического представления результатов моделирования используется функция plot

(см. п. 1.3.2).

Для построения гистограммы распределения используется функция hist.

n=hist(y) распределяет элементы вектора y в 10 интервалов одинаковой длины и возвра- щает количество элементов, попавших в каждый интервал, в виде вектора n. Если y – матри- ца, то hist работает со столбцами.

n=hist(y,l), где l – скаляр, использует l интервалов одинаковой длины.

n=hist(y,x), где x – вектор, возвращает количество элементов вектора y, попавших в ин- тервалы с центрами, заданными вектором x. Число интервалов в этом случае равно числу элементов вектора x.

[n,x]=hist(…) возвращает числа попаданий в интервалы (в векторе n), а также положения центров интервалов (в векторе x).

hist(…) строит гистограмму без возвращения параметров, т. е. строит прямоугольники

высотой

hi = mi ,

где mi – число элементов, попавших в i -й интервал, i = 1, l .

6.4.Порядок выполнения работы

6.4.1.Выполнить моделирование реализаций простейшего потока двумя приведенными в п. 6.2 алгоритмами. Вывести графическую иллюстрацию потоков в виде нанесенных на ось

абсцисс моментов появления требований и концов промежутка (a,b) . Параметры потока для моделирования взять из таблицы 6.1.

28

6.4.2.Вывести гистограмму промежутка времени между соседними требованиями потока

иего плотность вероятности. Для согласования масштабов гистограммы и генеральной плотности вероятности необходимо генеральную плотность вероятности умножить на коэф-

фициент

	k = n	(n) − (1)	,
		l

где n – объем выборки, l – число интервалов разбиения выборки при построении гисто- граммы, (1) , (n) – минимальный и максимальный из интервалов времени между требова- ниями соответственно.

6.4.3.Получить оценку λ параметра λ потока.

6.4.4.Оформить полученные результаты в виде отчета.

	Таблица 6.1. Параметры случайных потоков для моделирования
№		Параметр λ, интервал	№	Параметр λ, интервал
варианта		(a,b)	варианта	(a,b)
1.		λ =1, a = 0, b =100	11.	λ = 0.1, a = 0, b = 650
2.		λ = 2, a = 0, b = 90	12.	λ = 0.2, a = 0, b = 550
3.		λ = 3, a = 0, b = 80	13.	λ = 0.3, a = 0, b = 500
4.		λ = 4, a = 0, b = 70	14.	λ = 04 , a = 0, b = 450
5.		λ = 5, a = 0, b = 60	15.	λ = 0.5, a = 0, b = 400
6.		λ = 6 , a = 0, b = 50	16.	λ = 0.6, a = 0	, b = 350
7.		λ = 7 , a = 0, b = 40	17.	λ = 0.7 , a = 0	,b = 300
8.		λ = 8, a = 0, b = 30	18.	λ = 0.8, a = 0	, b = 200
9.		λ = 9 , a = 0, b = 25	19.	λ = 0.9, a = 0, b =150
10.		λ = 8, a = 0, b = 20	20.	λ = 0.8, a = 0, b =170

29

Тема 7. Случайный двоичный сигнал

7.1.Цель работы

7.1.1.Изучение цепей Маркова с непрерывным временем на примере случайного двоич- ного сигнала.

7.2.Теоретические положения

Рассмотрим конечную цепь Маркова с непрерывным временем и двумя состояниями Е1 и Е2 . Пусть эти состояния имеют численные значения E1 = −1 и E2 =1, причём вероятность

перехода за малое время t в другое состояние определяется условием
p1,2 ( t) = p2,1( t) = λ t + o( t).	(7.1)

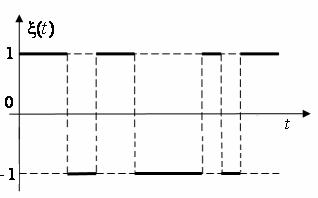
Такой процесс называется случайным телеграфным или случайным двоичным сигналом. Од- на из реализаций этого процесса приведена на рис. 7.1.

Рис. 7.1. Реализация случайного телеграфного сигнала

Условие (7.1) означат, что инфинитезимальная матрица процесса имеет следующий вид:

é− λ			λ ù
Q = ê	λ		ú .
ë		- λû
Матрица перехода P(t) имеет размер 2x2:
é p	(t)		p (t)ù
P(t) = ê 1,1			1,2	ú .
ë p2,1(t)			p2,2 (t)û
Найдём эту матрицу как решение прямой системы дифференциальных уравнений
		′			(7.2)
		P (t) = P(t)Q
с начальными условиями		é1	0ù
P(0) = I =
		ê	ú .
		ë0	1û

Известно, что решением этих уравнений является матричная экспонента, которая определят- ся как следующий ряд:

	P(t) = P(0)eQt = I(I + Qt +	1		(Qt)2	+	1		(Qt)3	+ ...)	(7.3)
		2!				3!

30