SlPr

Министерство образования Республики Беларусь

Учреждение образования БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

_______________________________________________________________

Кафедра информационных технологий автоматизированных систем

В. С. Муха

Случайные процессы

Практикум для студентов специальности 53 01 02 "Автоматизированные системы обработки информации"

всех форм обучения

Минск 2011

1

УДК 519.72 (075.8) ББК 22.172 я 73

М 92

Рецензент: профессор кафедры высшей математики БГУИР, кандидат физико- математических наук А.А. Карпук

Муха В.С.

М 92 Случайные процессы: Практикум для студ. спец. 53 01 02 "Автоматизирован- ные системы обработки информации" всех форм обучения / В.С. Муха. –

Мн.: БГУИР, 2011. – 49 с.: ил.

ISBN-985-444-581-Х

Практикум содержит описания семи тем практических занятий для за- крепления знаний по дисциплине «Случайные процессы». Выполнение практических занятий предполагает использование системы Matlab с па- кетом прикладных программ по статистике «Statistics Toolbox». Темы практических занятий содержат теоретическую часть, описание средств системы Matlab для решения поставленных задач, указания к порядку вы- полнения работы и варианты индивидуальных заданий.

УДК 519.72 (075.8) ББК 22.172 я 73

М 92

ISBN-985-444-581-Х	© Муха В.С., 2011
	© БГУИР, 2011

2

Тема 1. Моментные функции случайных процессов

1.1.Цель работы

1.1.1.Ознакомление с параметрической формой задания случайных процессов.

1.1.2.Приобретение навыков расчета математических ожиданий, дисперсий, ковариаци- онных и взаимных ковариационных функций случайных процессов.

1.2.Теоретические положения

Математическое ожидание aξ (t) , дисперсия dξ (t), ковариационная функция Rξ (t1,t2 ) случайного процесса ξ(t) определяются выражениями:

aξ (t) = E(ξ(t)),

dξ (t) = E((ξ(t) − aξ (t))2 ),

Rξ (t1,t2 ) = E((ξ(t1) − aξ (t1))(ξ(t2 ) − aξ (t2 ))).

Взаимные ковариационные функции двух процессов ξ(t) и η(t) определяются выражения-

ми

Rξ,η (t1,t2 ) = E((ξ(t1) − aξ (t1))(η(t2 ) − aη (t2 ))), Rη,ξ (t1,t2 ) = E((η(t1) − aη (t1))(ξ(t2 ) − aξ (t2 ))).

Здесь E – символ математического ожидания по соответствующему распределению.

Если случайные процессы ξ(t) и η(t) определены своими конечномерными плотностя-

ми вероятностей, то указанные моментные функции рассчитываются как следующие инте- гралы:

			∞			∞
	aξ (t) = ò xfξ (x,t)dx , aη (t) = ò xfη (x,t)dx ,
			−∞		∞	−∞
			dξ (t) =			− aξ (t)) fξ (x,t)dx ,
					ò(x
					−∞
			dη (t) =		∞	− aη (t)) fη (x,t)dx ,
					ò(x
			∞		−∞
	Rξ (t1,t2 ) =			− aξ (t1))( y − aξ (t2 )) fξ (x, y,t1,t2 )dxdy ,
			ò(x
		−∞
	Rη (t1,t2 ) =		∞	− aη (t1))(y − aη (t2 )) fη (x, y,t1,t2 )dxdy ,
			ò(x
		−∞
	Rξ,η (t1,t2 ) =	∞	∞
		ò	ò(x − aξ (t1))( y − aη (t2 )) fξ,η (x, y,t1,t2 )dxdy ,
		−∞ −∞
	Rη,ξ (t1,t2 ) =	∞	∞
		ò	ò(x − aη (t1))( y − aξ (t2 )) fη,ξ (x, y,t1,t2 )dxdy .

−∞ −∞

3

Здесь fξ (x,t) , fη(x,t) – одномерные плотности вероятностей случайных процессов ξ(t) и

η(t) соответственно, fξ (x, y,t1,t2) , fη (x, y,t1,t2 ) – двухмерные плотности вероятностей случайных процессов ξ(t) и η(t) соответственно, fξ,η(x, y,t1,t2) , fη,ξ (x, y,t1,t2 ) – вза- имные двухмерные плотности вероятностей случайных процессов ξ(t) и η(t) соответст- венно.

Если же случайные процессы ξ(t) и η(t) заданы в параметрической форме, т.е. в виде известных функций ξ(t,λ) и η(t,μ) векторных случайных параметров λ = (λ1,λ2 ,...,λm ) , μ = (μ1,μ2 ,...,μk ) , то указанные моментные функции рассчитываются как следующие ин- тегралы:

aξ (t) =		∞		∞
		òξ(t, z) fλ (z)dz , aη (t) = òη(t, z) fμ (v)dv ,
	−∞		∞	−∞
		dξ (t) =		− aξ (t)) fλ (z)dz ,
			ò(ξ(t, z)
			−∞
		dη (t) =	∞	− aη (t)) fμ (v)dv ,
			ò(η(t, z)
		∞	−∞
Rξ (t1,t2 ) =
		ò(ξ(t1, z) − aξ (t1))(ξ(t2 , z) − aξ (t2 )) fλ (z)dz ,
		−∞
Rη (t1,t2 ) =		∞
		ò(η(t1,v) − aη (t1))(η(t2 ,v) − aη (t2 )) fμ (v)dv ,
		−∞
Rξ,η (t1,t2 ) =	∞	∞
	ò	ò(ξ(t1, z) − aξ (t1))(η(t2 ,v) − aη (t2 )) fλ,μ (z,v)dzdv ,
	−∞ −∞
Rη,ξ (t1,t2 ) =	∞	∞
	ò	ò(η(t1,v) − aη (t1))(ξ(t2 , z) − aξ (t2 )) fλ,μ (z,v)dzdv .

−∞ −∞

Здесь fλ (z), fμ (v) – плотности вероятностей случайных векторов λ и μ соответственно, fλ,μ (z,v) , – совместная плотность вероятности случайных векторов λ и μ.

Если случайные векторы λ и μ независимые, то fλ,μ (z,v) = fλ (z) fμ (v) .

Как свойства приведенных выше интегралов легко могут быть получены следующие свойства моментных функций. Если

ζ(t) = ξ(t) ± η(t) ,

то

aζ (t) = aξ (t) ± aη (t),

dζ (t) = dξ (t) + dη (t) ± 2Rξ,η (t,t) ,

Rζ (t1,t2 ) = Rξ (t1,t2 ) + Rη (t1,t2 ) ± Rξ,η (t1,t2 ) ± Rη,ξ (t1,t2 ) .

Если случайные процессы ξ(t) и η(t) независимы, то в приведенных выше формулах

Rξ,η (t1,t2 ) = Rη,ξ (t1,t2 ) = 0.

Если случайные процессы ξ(t) и η(t) независимы и ζ(t) = ξ(t)η(t) , то

4

aζ (t) = aξ (t)aη (t) , dζ (t) = dξ (t)dη (t) ,

Rζ (t1,t2 ) = Rξ (t1,t2 )Rη (t1,t2 ) .

1.3. Программные средства для выполнения работы

1.3.1. Символьное вычисление интегралов

Для вычисления указанных выше интегралов можно воспользоваться функцией символь- ного интегрирования int.

int(s) – возвращает символьное значение неопределенного интеграла от символьного вы- ражения или массива символьных выражений s по переменной, которая автоматически опре- деляется функцией findsym. Если s – константа, то вычисляется интеграл по переменной 'x'; int(s,a,b) – возвращает символьное значение определенного интеграла на отрезке интег- рирования [a,b] от символьного выражения или массива символьных выражений s по пере- менной, которая автоматически определяется функцией findsym. Пределы интегрирования a, b могут быть как символьными, так и числовыми, как конечными, так и бесконечными (inf); int(s,v) – возвращает символьное значение неопределенного интеграла от символьного

выражения или массива выражений s по переменной v;

int(s,v,a,b) – возвращает символьное значение определенного интеграла от символьного

выражения или массива символьных выражений s по переменной v с пределами интегрирования [a,b].

Пример. Программа syms alpha u y2=int(sin(alpha*u),alpha)

возвращает следующий результат: y2 =

-cos(alpha*u)/u

1.3.2. Символьные подстановки

Часто в символьное выражение вместо некоторых переменной или выражения необходи- мо подставить новую переменную или выражения. В Matlab это можно сделать с помощью

функции subs.

y=subs(s,old,new) заменяет в символьном выражении s старую переменную или выраже-

ние old на новую переменную или выражение new. Пример. Программа

syms t tau y=sin(t);

y1=y*subs(y,t,t+tau)

возвращает следующий результат: y1 =

sin(t)*sin(t+tau)

1.3.3. Построение графиков функций одной переменной

Для построения графика функции одной переменной используется функция plot. Вызов

этой функции осуществляется командой plot(x,y,s)

где x, y – одномерные массивы одинаковой размерности; x – массив значений аргумента функции y = f (x) ; y – массив значений функции y = f (x) ; s – строковая константа, опре-

5

деляющая цвет линии, маркер узловых точек и тип линии. Эта константа может содержать от одного до трех символов.

Цвет линии определяется символами y (желтый), m (фиолетовый), c (голубой), r (крас- ный), g (зеленый), b (синий), w (белый), k (черный).

Тип узловой точки определяется символами . (точка), o (окружность), x (крестик), + (плюс), * (звездочка), s (квадрат), d (ромб), < > ^ (треугольники различной направленности), p (пя-

тиугольник), h (шестиугольник).

Тип линии определяется символами - (непрерывная), : (короткие штрихи), -. (штрих- пунктир), -- (длинные штрихи).

Символьную константу s можно опустить. В этом случае по умолчанию используется не- прерывная линия желтого цвета.

Для построения в одном окне нескольких графиков можно использовать команду plot(x1,y1,s1,x2,y2,s2,x3,y3,s3,…)

Команда grid on добавляет на график сетку. Команда hold on позволяет добавлять в то же графическое окно графики новых функций.

Пример

x=0:0.1:2*pi;

y1=sin(x);

y2=cos(x); plot(x,y1,'k-o',x,y2,'r--*') grid on

Созданный с помощью программы plot график можно скопировать в буфер Clipboard, акти- визировав в пункте Edit главного меню графического окна команду Copy Figure, с целью его дальнейшего редактирования в каком-либо графическом редакторе, например Paint.

1.3.4. Построение графиков функций двух переменных

Ковариационная функция нестационарного случайного процесса и взаимная ковариаци- онная функция двух случайных процессов являются функциями двух переменных. Построе- ние графика функции двух переменных z = f (x, y) выполняется в Matlab с помощью

функций meshgrid и mesh. Специфика построения таких графиков в Matlab требует не про- сто задания ряда значений x и y, т. е. векторов x и y, а определения двухмерных массивов X и Y. Для создания таких массивов служит функция meshgrid.

[X,Y]=meshgrid(x,y) – преобразует область, заданную векторами x и y, в двухмерные мас- сивы X и Y, которые могут быть использованы для вычисления значений функции двух пе- ременных и построения трехмерных графиков. Эта функция формирует массивы X и Y та- ким образом, что строки выходного массива X являются копиями вектора x, а столбцы вы- ходного массива Y – копиями вектора y.

mesh(X,Y,Z,C) – выводит в графическое окно сетчатую поверхность с цветами узлов по- верхности, заданных массивом С.

mesh(X,Y,Z) – аналог предшествующей команды при C=Z, с использованием функцио- нальной окраски, при которой цвет задается высотой поверхности.

Пример

[x,y]=meshgrid(-2:0.1:2,-2:0.1:2); z=x.^2+y.^2;

mesh(x,y,z)

В результате выполнения этой программы на экран будет выведен график функции двух пе- ременных z = x2 + y2 .

6

1.3.5. Моделирование случайных чисел

Случайные числа из равномерного распределения u(a,b) , плотность вероятности кото-

рого имеет вид

		ì	1
f		(x)= íï		,	a < x < b, a,bÎ R, a < b,
	ξ	ïb - a			x £ a, x ³ b,
		î	0,

моделируются с помощью функции y=unifrnd (a,b).

Непрерывный случайный вектор x = (x1,...,xm ) называется распределенным по много- мерному нормальному (гауссовскому) закону, если его плотность вероятности имеет вид

f

(X ) =

1

exp(-

1

j(X )),

ξ

2

(2p)m

R

где

j(X ) = (X - A)T R−1(X - A) .

Здесь приняты следующие

обозначения:

X T

= (x ,..., x

m

) – вектор-строка аргументов

AT = (a ,...,a

1

плотности

вероятности;

m

)

–

вектор-строка

параметров;

1

R = (Ri, j ), i, j =1, m , – симметричная положительно определенная (m × m) -матрица па-

раметров; R−1 – матрица, обратная матрице R; R – определитель матрицы R. Символ Т оз- начает транспонирование, так что X и A – векторы-столбцы. Параметры А и R распределе- ния являются математическим ожиданием и ковариационной матрицей вектора x соответст- венно.

Если случайный вектор x = (x1,...,xm ) распределен по нормальному закону, то любой

его подвектор (включая отдельную компоненту) также распределен по нормальному закону.

Распределение этого подвектора получается вычеркиванием в исходном распределении из

векторов		= (x ,...,x			), AT = (a ,...,a			) ненужных компонент и из матрицы R строк и
	x			m			m
1						1
столбцов, соответствующих ненужным компонентам.
Символически			многомерное			нормальное			распределение	обозначается	как
fξ (X ) = N(A, R).

Если x = (x1,x2 ) – двухмерный случайный вектор, распределенный по нормальному закону, то мы имеем

T

T

æ

R

R

ö

= (x1

, x2 ) ,

= (a1,a2) ,

ç

1,1

1,2

÷

X

A

R = ç R

2,1

R

÷,

è

2,2

ø

−1

æ R

2,2

- R

ö

R

= R1,1R2,2

- R1,2 R2,1,

R

=

1 ç

1,2 ÷

,

R

ç

- R

2,1

R

÷

è

1,1

ø

j(X )= (X - A)T R−1(X - A) =

= R (x - a )2

- 2R (x - a )(x - a

) + R (x - a

)2 .

2,2

1

1

1,2

1

1

2

2

1,1

2

2

Если

здесь обозначить R

= s2 ,

R

= s2

и

выразить

коэффициент ковариации

1,1

1

2,2

2

R1,2

= R2,1 = cov(ξ1,ξ2 ) через коэффициент корреляции r1,2 по формуле

7

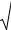
то функцию ϕ(X )

R1,2 = R2,1 = r1,2σ1σ2 ,

можно представить в виде

1

æ

(x - a )2

(x - a ) (x

2

- a

2

)

(x

2

- a

2

)2

ö

j(x , x

) =

ç

1 1

- 2r

1 1

+

÷

,

(1 - r2

s2

s1

s2

s2

1

2

) ç

1,2

÷

1,2

è

1

2

ø

а плотность вероятности двухмерного нормального распределения – в виде

				1		æ			1		ö
	f		(x1, x2 ) =				expç	-		j(x1	, x2 )÷ .
		ξ
									2
				2ps1s2 1- r12,2
						è					ø

Функция r=mvnrnd(mu,sigma,cases) возвращает матрицу r случайных чисел, выбранных

из многомерного нормального распределения с вектором средних mu и ковариационной матрицей sigma. Параметр cases является количеством строк в r (количеством многомерных случайных чисел).

1.4.Порядок выполнения работы

1.4.1.Рассчитать функции математического ожидания, дисперсии и ковариационной функции случайного процесса ζ(t) , выбранного из таблицы 1.1 в соответствии со своим ва-

риантом задания. Вид составляющих случайного процесса ζ(t) и распределения их пара-

метров заданы в таблице 1.2.	Параметры λ = (b,c,d) ,	ϕ , ω предполагаются случайными
величинами, независимыми	в совокупности. В	символьных расчетах параметры
b, c, d, ϕ, ω рассматривать как символьные переменные.

1.4.2. В одно графическое окно вывести 10 реализаций случайного процесса ζ(t) и функ- ции математического ожидания и дисперсии, моделируя случайные значения параметров

b, c, d, ϕ, ω

и

выбирая

по

своему

усмотрению

значения

неслучайных параметров

a

b

, a

c

, a

d

, A, B , s2 , σ2

, σ2

, σ2 , ω и интервал времени t

0

≤ t ≤ t .

b

c

d

1

1

1.4.3. В отдельное графическое окно вывести график ковариационной функции случайно-

го процесса

ζ(t)

при выбранных значениях неслучайных параметров ab , ac , ad , A, B ,

s2 , σb2 , σc2 , σ2d , ω1 .

1.4.4.Оформить полученные результаты в виде отчета.

Таблица 1.1. Варианты случайных процессов ζ(t) для расчетов

№	Процесс ζ(t)	№	Процесс ζ(t)
варианта		варианта
1.	ξ(t) + η(t)	11.	ξ(t)η(t)
2.	ξ(t) + θ(t)	12.	ξ(t)θ(t)
3.	ξ(t) + ψ(t)	13.	ξ(t)ψ(t)
4.	ξ(t) + χ(t)	14.	ξ(t)χ(t)
5.	η(t) + θ(t)	15.	η(t)θ(t)
6.	η(t) + ψ(t)	16.	η(t)ψ(t)
7.	η(t) + χ(t)	17.	η(t)χ(t)
8.	θ(t) + ψ(t)	18.	θ(t)ψ(t)

8

9.

θ(t) + χ(t)

19.

θ(t)χ(t)

10.

ψ(t) + χ(t)

20.

ψ(t)χ(t)

Таблица 1.2. Составляющие случайного процесса ζ(t) , заданного в таблице 1.1

№

Случайный пара-

Обозначение распределения пара-

процес-

Вид процесса

метр

метра

са

1

ξ(t) = b

b

λ = (b,c,d) ,

2

η(t) = ct

c

fλ (x) = N(aλ , Rλ ),

aλ = (ab ,ac ,ad ) ,

θ(t) = σ2 exp(−dt)

ésb2

0

0

ù

3

d

R

= ê

0

s2

0

ú

λ

ê

c

ú

ê

0

0

s2

ú

ë

d

û

4

ψ(t) = Acos(ω1t + ϕ)

ϕ

U (−a,a)

5

χ(t) = Bcosωt

ω

U (0,a)

9

Тема 2. Моделирование случайных событий и дискретных случайных величин

2.1.Цель работы

2.1.1.Приобретение навыков моделирования полной группы случайных событий.

2.1.2.Приобретение навыков моделирования случайных чисел из дискретных распределе-

ний.

2.2.Теоретические положения

2.2.1.Моделирование полной группы случайных событий

Случайные события Ai F , P(Ai ) = pi , i =1,k , заданные на вероятностном простран- стве (Ω, F, P) , образуют полную группу событий, если выполняются условия:

k		k
а) U Ai = Ω ; б) Ai I Aj = Ο, i ¹ j ; в) P(Ai ) ³ 0, i =	1,k	; г) åP(Ai ) =1.
i =1		i =1

Для моделирования полной группы случайных событий будем использовать базовую слу- чайную величину α , т.е. непрерывную случайную величину, распределенную равномерно в

интервале (0,1) . По вероятностям pi	случайных событий Ai определим числа
	i
	S0 = 0 , Si = å p j ,			(2.1)
	j =1
а события Ai определим как следующие множества:
Ai	= (Si −1 £ a < Si ), i =		.
		1,k		(2.2)

Построенные таким образом события удовлетворяют сформулированным выше условиям а)

– г). Действительно,

Si	Si
P(Ai ) = ò fα (x)dx = òdx = Si − Si−1		= pi , i =	1,k	.
Si−1	Si−1

Алгоритм, моделирующий отдельное случайное событие Ai (его номер i ), состоит в вы- полнении следующих шагов.

1.Расчет чисел S0 ,S1,...,Sk по формуле (2.1).

2.Обращение к датчику базового случайного числа и получение псевдослучайного чис-

ла α .

3.Сравнение α с величинами S0 ,S1,...,Sk и выбор номера события i , удовлетворяю-

щего условию (2.2).

Для моделирования результатов n независимых испытаний, в каждом из которых может появиться одно из событий A1, A2 ,..., Ak , пункты 2,3 алгоритма необходимо повторить n раз.

2.2.2. Моделирования случайных чисел из дискретных распределений

Пусть ξ – дискретная случайная величина, принимающая значения x1, x2 ,..., xk с веро- ятностями p1, p2 ,..., pk . Моделировать значения этой случайной величины можно с помо- щью алгоритма моделирования полной группы случайных событий, изложенного в п. 2.2.1. Действительно, между значениями xi дискретной случайной величины и случайными собы-

10