Функция figure

Функция figure имеет следующий синтаксис: figure(n),

где n – индекс окна вывода.

Данная функция делает активным окно вывода с индексом n, т.е. дальнейший вывод графической информации будет осуществляться в данном окне, пока не встретится функция figure с другим индексом окна вывода. Если окна с данным индексом не существует, то оно предварительно создается.

Функция subplot

Функция subplot предназначена для разбиения активного окна на области и выбора активной области для вывода графических данных. Функция subplot имеет следующий формат:

subplot(mnp)

subplot(m,n,p),

где m указывает на сколько частей разбивается окно по вертикали, n – по горизонтали, p определяет номер области, в которую будут выводиться графические данные. Если числа n, m и p находятся в диапазоне от 1 до 9, то они обычно пишутся слитно (первый вариант записи функции), в противном случае они разделяются запятыми (второй вариант). Пример:

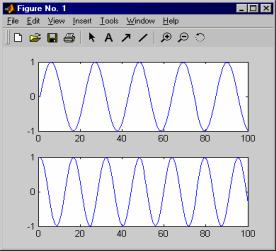
n = 0:99

x = sin(0.3*n) y = cos(0.4*n) subplot(211) plot(x) subplot(212) plot(y)

Данная программа разбивает окно вывода на 2 части по вертикали и выводит график x в верхней части, а график y в нижней. Результат работы данной программы показан на рисунке 3.

Рисунок 3 – Результат работы программы, демонстрирующей работу функции subplot.

Базовые сигналы ЦОС

Наиболее важными последовательностями, которые часто используются в цифровой обработке сигналов, являются:

1. Единичный импульс

δ0	1,	n = 0,
	(n) =	n ≠ 0.
	0,

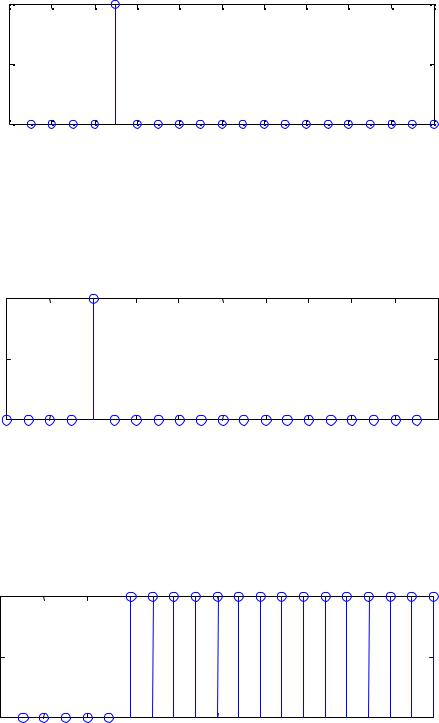
Единичный импульс показан на рисунке 4

1

0.5

0	-4	-2	0	2	4	6	8	10	12	14
-6

Рисунок 4 – Единичный импульс 2. Единичный импульс, задержанный на n0 отсчетов:

δ0	1,	n = n0 ,
	(n − n0 ) =	n ≠ n0 .
	0,

Данная функция показана на рисунке 5.

1

0.5

00 n0

Рисунок 5 – Единичный импульс δ0 (n − n0 ) . 3. Единичный скачок:

u−1	1,	n ≥ 0,
	(n) =	n < 0.
	0,

Данная функция показана на рисунке 6.

1

0.5

0	-4	-2	0	2	4	6	8	10	12	14
-6

Рисунок 6 – Единичный скачок

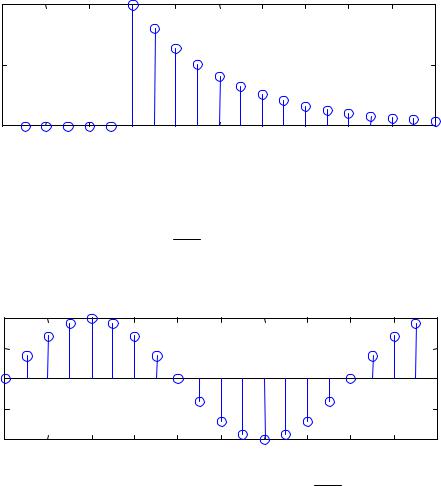
4. Убывающая экспонента:
		n	, n ≥ 0,
g(n) = a
	0, n < 0.

Данная функция показана на рисунке 7.

1

0.5
0	-4	-2	0	2	4		6	8	10	12	14
-6
	Рисунок 7 – Убывающая экспонента (a = 0,8)
5. Косинусоида:
				2πn			= A cos(ωn +ϕ).
					+ϕ
		h(n) = A cos		n0
Данная функция показана на рисунке 8.
1
0.5
0
-0.5
-1	-2	0	2	4	6		8	10	12	14	16
-4
									2πn
		Рисунок 8 – Косинусоида						cos
									16 .

6. Комплексная экспонента:

e jωn = cos(ωn) + j sin(ωn).

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Сформируйте и постройте график следующих последовательностей:

x1[n] = a1	δ[n–b1],	n = 1..20,
x2[n] = a2	δ[n],	n = -15..15,
x3[n] = a3	δ[n–b3],	n = 300..350,
x4[n] = a4	δ[n+b4],	n = -10..0.

Значения a1…a4 и b1…b4 выбираются согласно следующей таблицы:

Номер варианта	1	2	3	4	5	6
a1	1,2	1,3	1,4	1,5	1,6	1,7
b1	4	5	6	7	8	9
a2	0.6	0.7	0.8	0.9	1.1	1.2
a3	1.8	1.7	1.6	1.5	1.4	1.3
b3	310	312	318	321	328	333
a4	3.8	4.0	4.2	4.4	4.6	4.8
b4	3	4	5	6	7	8

2. Использованная со временным сдвигом последовательность δ[n-n0] позволяет построить периодический сигнал с периодом P и общей длиной MP:

s[n]= M∑−1 Alδ[n −lP],

l=0

где Al – весовые коэффициенты. Сформируйте и постройте c помощью функции stem график периодической импульсной последовательности с P=5 и общей длиной 50. Сделайте это сначала с помощью цикла for, а затем с помощью векторных операций.

3. Сформируйте и постройте графики следующих последовательностей. Используйте для этого возможности вычисления синуса или косинуса от векторного аргумента:

x1[n] = sin(a1n),		n = 0..25,
x2[n] = sin(a1n),		n = -15..25,
x3[n] = sin(a2n + π/2),		n = -10..10,
x4[n] = cos(a3n),		n = 0..50.
Значения a1…a3 выбираются согласно следующей таблицы:
Номер варианта	1	2	3	4	5	6
a1	π/13	π/14	π/15	π/16	π/17	π/18
a1	π	2π	3π	π	2π	3π
a3	π/ 19	π/ 21	π/ 23	π/ 20	π/ 22	π/ 18

Упростите x3, чтобы не использовать тригонометрические функции.

4.Напишите функцию для формирования синусоиды конечной длины. Функция должна иметь 5 входных аргументов: 3 параметра синусоиды, начальное и конечное значения n. Проверьте работу этой функции.

5.Сформируйте синусоиду дискретного времени дискретизацией синусоиды непрерывного времени со следующими параметрами:

Номер варианта	1	2	3	4	5	6
Частота сигнала	900 Гц	1 кГц	1,1 кГц	1,3 кГц	1,4 кГц	1,5 кГц
Начальная фаза	45˚	60˚	30˚	45˚	60˚	30˚
Нормализованная	40	45	50	55	60	65
амплитуда
Частота дискретизации	8 кГц	8 кГц	8 кГц	10 кГц	10 кГц	10 кГц
Начальное время	0 сек	0 сек	0 сек	0 сек	0 сек	0 сек
Конечное время	6 мсек	7 мсек	8 мсек	4 мсек	5 мсек	6 мсек

6. Изучите функцию, генерирующую экспоненту дискретного времени: function y=genexp(b,n0,L)

if (L<=0)

error(‘длина неверна’) end

nn=n0+[1:L]`-1; y=b.^nn;

Используйте данную функцию для построения x[n] = an при n = 0..20, где

Номер варианта	1	2	3	4	5	6
a	0,7	0,75	0,8	0,85	0,9	0,95

7. Другой способ формирования экспоненциального сигнала – использование разностных уравнений. Сигнал y[n] = an u[n] является решением следующего разностного уравнения:

y[n] - a y[n-1] = x[n],

где x[n] – единичный импульс; начальное значение y[-1]=0.

Смысл разностного уравнения заключается в вычислении y[n] для последовательных n, начиная с n= -1.

Используйте функцию Matlab filter для формирования того же сигнала, что и в задании 6.

8. Для формирования комплексной экспоненты может быть использована формула Эйлера:

x[n] = (z0)n = rn ejθn = rn (cos θn + j sin θn).

Используйте данное выражение со следующими параметрами:

Номер варианта	1	2	3	4	5	6
r	0,7	0,75	0,8	0,85	0,9	0,95
θ	30°	45°	60°	30°	45°	60°

Постройте график действительной и мнимой части для n = 0…20. Как сказывается изменение θ? Постройте график, откладывая по оси ординат действительную часть, а по оси абсцисс – мнимую (должна получиться спираль). Поэкспериментируйте с углом θ для получения спиралей различного вида.

9. Формула Эйлера не позволяет получить все возможные варианты ком-

плексной экспоненты. Более общим выражением является

G (z0)n = A ejφ rn ejθn = A rn (cos(θn+φ) + j sin(θn+φ)),

где G = A ejφ – комплексная амплитуда комплексной экспоненты. Сформируйте и постройте графики следующих последовательностей.

Преобразуйте синусоиды в комплексную нотацию. Для формирования сигналов используйте функцию exp. Если сигнал действительный, он должен генерироваться как действительная часть комплексного сигнала:

x1[n] = a1 sin(f1n) +j a2 cos(f1n),						n = 0..20,
x2[n] = sin(f2n),						n = -15..25,
x3[n] = a3n cos(f3n+π/4),						n = 0..50,
x4[n] = a4n cos(f3n) ,						n = -10..20.
Значения a1…a4, f1…f3 выбираются согласно следующей таблицы:
Номер варианта	1		2		3		4	5		6
a1	2		3		1		3	1		2
a2	1		2		3		1	2		3
f1	π/7		π/6		π/5		π/8	π/9		π/7
f2	π/17		π/18		π/19		π/20	π/15		π/16
a3	1,1		1,2		1,3		0,9	0,8		0,7
f3	π/11		π/12		π/13		π/14	π/10		π/15
a4	0,9		0,8		0,7		1,1	1,2		1,3

Для каждого сигнала определите амплитуду и фазу G и z0.

10. Комплексная экспонента может быть сгенерирована разностным уравнением первого порядка (с использованием функции filter):

y[n] = z0 y[n-1] + x[n].

Коэффициент фильтра z0 = r ejθ – комплексное число.

Воспользуйтесь функцией filter для формирования тех же сигналов, что и в предыдущем задании. Проверьте работу, построив графики действительной и мнимой частей.