
- •Раздел 1. Основные элементы функционального анализа. Функциональные пространства
- •§1.1. Линейное пространство
- •§1.3. Евклидово пространство
- •§1.4. Метрические пространства
- •§1.6. Пространство Гильберта
- •§2.2. Линейные операторы в конечномерных линейных пространствах и их матрицы
- •§2.3. Интегральные и дифференциальные операторы. Функционалы
- •Раздел 3. Специальные функции и их приложения
- •§3.1. Определенные интегралы, зависящие от параметра, и их свойства
- •§ 4.1. Решетчатые функции. Z -преобразование и его свойства
- •§5.2. Простейшая задача вариационного исчисления
- •§6.2. Классификация и приведение к каноническому виду линейных уравнений в частных производных второго порядка с двумя независимыми переменными в окрестности точки
Министерство образования Республики Беларусь Учреждение образования
«Белорусский государственный университет информатики и радиоэлектроники»
Кафедра высшей математики
СПЕЦИАЛЬНЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ
И ФУНКЦИИ
Методическое пособие для студентов специальностей 1-45 01 01 «Многоканальные системы телеком-
муникаций», 1-45 01 02 «Системы радиосвязи, радиовещания
ителевидения», 1-53 01 07 «Информационные технологии и управление
втехнических системах» заочной формы обучения
Минск БГУИР 2011
УДК 517.9(076) ББК 22.16я73 С71
Авторы:
В. В. Цегельник, З. Н. Четыркина, В. А. Ранцевич, Н. В. Спичекова, З. Н. Примичева
Рецензент: заведующий кафедрой информатики
учреждения образования «Белорусский государственный университет информатики и радиоэлектроники», доктор физико-математических наук, профессор Л. И. Минченко
Специальные математические методы и функции : метод. посоС71 бие для студ. спец. 1-45 01 01 «Многоканальные системы телекоммуникаций», 1-45 01 02 «Системы радиосвязи, радиовещания и телевидения», 1-53 01 07 «Информационные технологии и управление в технических системах» заоч. формы обуч. / В. В. Цегельник [и др.]. – Минск :
БГУИР, 2011. – 76 с.
ISBN 978-985-488-708-1.
Дано краткое изложение теоретического материала, а также примеры решений типовых задач с использованием специальных математических методов. Содержит 10 вариантов контрольной работы, методические указания к ее выполнению и список литературы.
Для самостоятельного изучения специальных математических методов и функций студентами-заочниками. Может быть использовано и при проведении занятий со студентами дневной формы обучения, где изучается указанная дисциплина.
УДК 517.9(076) ББК 22.16я73
ISBN 978-985-488-708-1 |
© УО «Белорусский государственный |
|
университет информатики |
|
и радиоэлектроники», 2011 |
2
Содержание |
|
Введение ………………………………………………………………..... |
4 |
Раздел 1. Основные элементы функционального анализа. |
|
Функциональные пространства ……………………………………….............. |
4 |
§1.1. Линейное пространство ………………………………………….. |
4 |
§1.2. Линейная зависимость и независимость системы векторов. |
|
Базис и размерность линейного пространства ……………………………….. |
6 |
§1.3. Евклидово пространство …………………………………………. |
7 |
§1.4. Метрические пространства …………………………………….... |
9 |
§1.5. Полнота метрического пространства (X, ) …………………… |
12 |
§1.6. Пространство Гильберта …………………………………………. |
12 |
§1.7. Обобщенный ряд Фурье ………………………………………….. |
15 |
§1.8. Ортогональные системы функций ………………………………. |
17 |
Раздел 2. Линейные операторы. Функционалы ……………………….. |
21 |
§2.1. Введение …………………………………………………………... |
21 |
§2.2. Линейные операторы в конечномерных линейных |
|
пространствах и их матрицы ………………………………………………….. |
22 |
§2.3. Интегральные и дифференциальные операторы. Функционалы …. |
26 |
Раздел 3. Специальные функции и их приложения …………………… |
29 |
§3.1. Определенные интегралы, зависящие от параметра, и их |
|
свойства …………………………………………………………………………. |
29 |
§3.2. Эйлеровы функции (x) и B(x, y) ……………………………... |
31 |
Раздел 4. Решетчатые функции. Z-преобразование и его приложения... |
33 |
§4.1. Решетчатые функции. Z-преобразование и его свойства ………. |
33 |
§4.2. Разностные уравнения. Решение разностных уравнений |
|
с помощью Z-преобразования ………………………………………………… |
37 |
Раздел 5. Элементы вариационного исчисления ………………………... |
39 |
§5.1. Первоначальные понятия ………………………………………… |
39 |
§5.2. Простейшая задача вариационного исчисления ………………... |
40 |
§5.3. Задача Бернулли о брахистохроне ………………………………. |
42 |
Раздел 6. Уравнения математической физики ………………………… |
44 |
§6.1. Понятия дифференциального уравнения в частных |
|
производных второго порядка с двумя независимыми переменными и его |
|
решения................................................................................................................. |
44 |
§6.2. Классификация и приведение к каноническому виду линейных |
|
уравнений в частных производных второго порядка с двумя независимыми |
|
переменными в окрестности точки …………………………………………… |
45 |
§6.3. Уравнение малых поперечных колебаний струны. Граничные |
|
и начальные условия. Корректность постановки задачи ……………………. |
48 |
§6.4. Решение уравнений свободных колебаний однородной струны |
|
методом Даламбера ……………………………………………………………. |
50 |
§6.5. Решение уравнений колебаний струны методом Фурье ……….. |
52 |
Методические указания к выполнению контрольной работы ……….. |
63 |
Литература ……………………………………………………………….. |
69 |
Контрольная работа ……………………………………………………... |
70 |
3

Введение
Радиоинженеру традиционно приходится иметь дело с сигналами. С математической точки зрения сигнал представляет собой временную функцию. Поэтому для успешной обработки сигнала необходимо понять, что такое сигнал; какие у него могут быть математические характеристики; что значит «два сигнала близки друг к другу»; как понять «расстояние» между сигналами. Для того чтобы найти связь между указанными характеристиками, а также выяснить границы их применимости, необходимо освоить ряд вспомогательных математических понятий и методов исследования, которые не входят в классический курс «Высшая математика». Поэтому на кафедре высшей математики разработана дисциплина «Специальные математические методы и функции», относящаяся к разделу «Специальные главы высшей математики».
Раздел 1. Основные элементы функционального анализа. Функциональные пространства
§1.1. Линейное пространство
В математике важную роль играет понятие пространства, т. е. множества, между элементами которого аксиоматически заданы некоторые соотношения. В этом случае говорят, что на множестве задана структура соответствующего пространства.
Определение 1.1. Линейным (или векторным) пространством L называ-
ется всякая совокупность объектов (элементов)
L x, y,..., z,...,u,... ,
условно называемых векторами, над которым определены две операции –
сложения : x, y L, x y z L, и умножения на число : x L,
P (P – некоторое числовое множество), x u L, подчиняющиеся следующим аксиомам:
1º. |
|
|
x |
|
y |
|
y |
|
|
|
x |
|
– коммутативность сложения; |
||||||||||||||||||||||||||||||||||||||||||||||||
2º. |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
z |
– ассоциативность сложения; |
|||||||||||||||||||||||||||||||||||||||||||
x |
y |
x |
y |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3º. |
|
существует нуль-вектор: |
|
|
|
0 |
|
|
для любого |
|
L; |
||||||||||||||||||||||||||||||||||||||||||||||||||
x |
x |
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4º. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
для каждого вектора x существует противоположный x , такой, что |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
x |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5º. |
|
x |
|
x |
|
|
– умножение на единицу; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
6º. |
|
( ) |
|
|
|
|
|
|
|
|
|
, где и – действительные или ком- |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
x |
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
плексные числа; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7º. |
|
( |
|
|
|
|
) |
|
|
|
; |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
y |
x |
y |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8º. |
|
( |
|
) ( ) |
|
– ассоциативный закон относительно про- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
изведения чисел.
4
Из аксиом 5º – 8º следует, что 0 x 0 для x L, 0 0 для
P.
В зависимости от того, какому из множеств принадлежат числа P – множеству действительных чисел R или множеству комплексных чисел C, пространство L называется соответственно действительным или комплексным линейным пространством. Элементы линейного пространства называются векторами, а само пространство – векторным.
Пример 1.1. Исследовать на линейность множество векторов трехмерно-
го пространства R3, исходящих из точки O. |
|
|
|
|
|
|
Решение. |
|
z |
|
|
|
|
Так как сумма двух таких векторов есть вектор, выхо- |
|
|
|
|
|
|
|
|
y |
||||
дящий из точки O, и произведение вектора на любое дейст- |
|
|
|
|||
|
|
|
|
|
|
|
вительное число также является вектором заданного множе- |
|
|
|
|
|
|
ства, то операции сложения и умножения на число опреде- |
|
|
|
|
|
|
лены на множестве векторов, исходящих из точки O трех- |
O |
|
|
|||
x |
||||||
мерного пространства R3, которые, можно показать, удов-
летворяют аксиомам 1º – 8º, и, следовательно, пространство R3 будет линейным пространством.
Пример 1.2. Доказать, что совокупность всех многочленов степени не
выше n a |
tn a tn 1 ... a |
t a |
n |
образует линейное пространство L от- |
|||||||
0 |
1 |
n 1 |
|
|
|
|
|
|
|
|
|
носительно обычных операций сложения и умножения на число. |
|
|
|
|
|||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
Сумма многочленов степени не выше n является мно- |
|
z |
|
|
|
|
|
||||
|
|
y |
|||||||||
гочленом степени не выше n. Произведение любого много- |
|
|
|
||||||||
|
|
|
|
|
|
|
|||||
члена из данного множества на число (действительное или |
|
|
|
|
|
|
|
||||
комплексное) не изменит степень многочлена. Таким обра- |
|
|
|
|
|
|
|
||||
зом, операции сложения и умножения на число определены |
O |
|
|
|
|||||||
x |
|||||||||||
на множестве многочленов степени не выше n и удовлетво- |
|
|
|
|
|
|
|
||||
ряют аксиомам 1º – 8º. Данное множество является линейным пространством. Аналогично можно доказать, что линейными пространствами являются: 1) множество всех решений y(x) линейного однородного дифференци-
ального уравнения
L(y(x)) y(n) a1y(n 1) |
... an 1y an y 0; |
|
|
||||||
2) множество C[a,b] {f (x),g(x),...} |
всех функций, |
непрерывных на от- |
|||||||
резке [a,b], с обычными операциями сложенияи умножения на число; |
|||||||||
a a |
|
b b |
|
|
|
||||
|
11 |
1n |
|
|
11 |
1n |
|
|
|
|
|
, |
|
|
размерности |
||||
3) множество всех матриц M |
,... |
||||||||
a a |
|
b b |
|
|
|
||||
|
m1 |
mn |
|
m1 |
mn |
|
|
||
|
|
|
|||||||
m n с обычными операциями сложения матриц и умножения матрицы на число.
5

§1.2. Линейная зависимость и независимость системы векторов. Базис и размерность линейного пространства
Пусть V – линейное векторное пространство.
Определение 1.2. Вектор b V называется линейной комбинацией век-
торов a1, a2,..., am, если найдется такой набор чисел 1, 2,..., m , при котором справедливо равенство
b 1,a1 2 ,a2 ... m ,am .
Определение 1.3. Система векторов a1, a2,..., am называется линейно зависимой, если равенство
1,a1 2 ,a2 ... m ,am 0
может быть выполнено хотя бы для одного ненулевого набора чисел
( 1, 2,..., m) (0,0,...,0).
Определение 1.4. Система векторов a1, a2,...am называется линейно независимой, если равенство
1,a1 2 ,a2 ... m ,am 0
выполняется тогда и только тогда, когда
Определение 1.5. Базисом линейного пространства V называется упорядоченная система максимального числа линейно независимых векторов.
Количество базисных векторов определяет размерность пространстваen,
которая обозначается . Если e1, e2,...,en – базис линейного пространства
V , то оно называется n-мерным и обозначается Vn , а всякий его вектор x можно представить в виде
x x1e1 x2e2 ... xnen .
Числа x1, x2,..., xn называют координатами вектора x в данном базисе. Например, в трехмерном пространстве в декартовой системе координат
базис образуют векторы i, j, k . Тогда любой вектор x представляется в виде их линейной комбинации
x x1i x2 j x3k .
Числа x1, x2, x3 – координаты вектора x в этом базисе.
В линейном пространстве многочленов степени не выше n в качестве ба-
зисных векторов можно взять набор многочленов B {xn, xn 1,..., x,1}. Тогда любой многочлен P(x) представляет собой линейную комбинацию элементов множества B:
P(x) a0xn a1xn 1 ... an 1x an 1.
Коэффициенты a0, a1,..., an 1, an являются координатами многочлена P(x) в базисе B.
6
Для |
множества |
матриц |
|
M (aij |
), ... , i |
|
, j |
|
, базисными |
|||||
|
1, m |
1, n |
||||||||||||
будут матрицы |
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 0 |
|
|
0...0 |
0 |
|
0 |
0 0 |
|||||
|
|
|
... |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
E11 |
0 |
0 0 |
,..., Eij i |
|
0 1 |
0 |
|
,..., Emn |
0 |
0 0 |
||||
|
|
|
. |
|||||||||||
0 0 0 .. 0 0 1
0...0 0
Вматрице Eij единица стоит на пересечении i-й строки и j-го столбца, а
все остальные элементы – нули. Тогда любая матрица (aij ) представляется в
виде суммы:
(aij ) a11E11 ... aijEij ... amnEmn .
Определение 1.6. Линейное пространство V называется бесконечномерным, если в нем существуют системы из любого числа линейно независимых векторов.
Примером такого бесконечномерного линейного пространства может служить множество всех аналитических (бесконечное число раз дифференци-
руемых) функций V C f (x), (x),... . В качестве базиса в этом про-
странстве можно взять набор простейших многочленов 1, x, x2,..., xn,... . Замечание 1. Все линейные пространства размерности n имеют одинако-
вые свойства. Поэтому достаточно изучить свойства арифметического линейного пространства An, элементы которого представляют собой упорядоченный набор n вещественных чисел:
An {x(x1, x2,..., xn)| xi R}.
Векторы e1 (1, 0,...,0), e2 (0,1,..., 0),...,en (0, 0,...,0,1) образуют базис пространства An.
§1.3. Евклидово пространство
Определение 1.7. Действительное линейное пространство L называется евклидовым, если каждой паре векторов x и y из L ставится в соответствие вещественное число (x, y) и выполняются аксиомы:
1º. (x,y) (y, x), x,y L;
2º. (x1 x2, y) (x1, y) (x2, y), x1, x2, y L; 3º. ( x, y) (x, y), R, x,y L;
4º. (x,x) x2 0, x L;(x,x) 0 x 0.
Число (x, y) называется скалярным произведением векторов x и y,
7

– скалярным квадратом вектора x (обозначается x2 ).
Аксиома 1º требует, чтобы скалярное произведение было коммутативно, т. е. не зависело от порядка сомножителей. Аксиомы 2º и 3º указывают на линейность этой операции по каждому аргументу.
Как известно, в декартовой системе координат в трехмерном векторном пространстве R3 скалярное произведение векторов a(ax,ay,az) и b(bx,by,bz)
может быть найдено по формуле:
(a,b) axbx ayby azbz |a ||b |cos (a ,b).
С помощью скалярного произведения для каждого вектора a естественным образом находится длина
|a | 
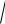 (a, a)
(a, a) 
 ax2 a2y az2
ax2 a2y az2
и для любых векторов a и b легко определяется угол между ними:
(a, b)arccos .
.
|a | |b |
Пространство R3 и операция скалярного произведения в этом пространстве были известны еще во времена Евклида, который жил в IV веке до нашей
эры. Поэтому R3с введенной операцией скалярного произведения называется
евклидовым пространством и обозначается E3.
С помощью скалярного произведения в евклидовом пространстве по аналогии с трехмерным евклидовым пространством E3 определяются следующие понятия:
1) норма вектора x (норма является аналогом длины вектора в обычном пространстве R3): 
 x
x


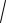 (x, x) ;
(x, x) ;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
x |
, |
|
y |
) |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
2) угол между векторами |
x |
и |
|
: cos ( |
x |
, |
|
y |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
y |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
3) расстояние между векторами |
|
и |
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
, |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
, |
|
|
|
) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
y |
x |
y |
x |
y |
x |
y |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Определение 1.8. Два вектора |
|
|
|
и |
|
|
|
называются ортогональными, если |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
y |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
их скалярное произведение равно нулю: ( |
|
|
, |
|
) 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Определение 1.9. Базис { |
e1*, |
e2*,..., |
en*} называется ортонормированным, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
если |
|
|
все |
|
векторы |
данного |
|
|
|
|
|
базиса |
|
имеют единичную |
длину |
(норму): |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
e1 * |
|
|
|
|
e2 * |
|
... |
|
|
en * |
|
, |
|
и попарно |
|
|
|
|
|
|
|
|
|
ортогональны |
друг |
к другу: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
( |
|
|
j*) 0, если i |
j, i, j |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
ei*, |
e |
1, n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
По любому базису можно построить ортонормированный базис, следуя нижеизложенному алгоритму.
8
