
Интерполирование на отрезке [0.801,1.2]
m = 20:

Приведем 1-е 15 и последние 15 точек.
|
i |
xi |
yi |
P(x) |
|
801 |
0,801 |
6,8297 |
6,8368 |
|
802 |
0,802 |
6,8162 |
6,8250 |
|
803 |
0,803 |
6,8124 |
6,8127 |
|
804 |
0,804 |
6,7998 |
6,7998 |
|
805 |
0,805 |
6,7865 |
6,7865 |
|
806 |
0,806 |
6,7728 |
6,7727 |
|
807 |
0,807 |
6,7587 |
6,7584 |
|
808 |
0,808 |
6,7440 |
6,7437 |
|
809 |
0,809 |
6,7289 |
6,7286 |
|
810 |
0,81 |
6,7115 |
6,7131 |
|
811 |
0,811 |
6,6952 |
6,6972 |
|
812 |
0,812 |
6,6787 |
6,6809 |
|
813 |
0,813 |
6,6618 |
6,6643 |
|
814 |
0,814 |
6,6447 |
6,6474 |
|
815 |
0,815 |
6,6274 |
6,6302 |
|
………………………………………………………………… |
|||
|
1186 |
1,186 |
5,8896 |
5,8889 |
|
1187 |
1,187 |
5,8920 |
5,8915 |
|
1188 |
1,188 |
5,8945 |
5,8941 |
|
1189 |
1,189 |
5,8970 |
5,8968 |
|
1190 |
1,19 |
5,8995 |
5,8995 |
|
1191 |
1,191 |
5,9021 |
5,9022 |
|
1192 |
1,192 |
5,9048 |
5,9051 |
|
1193 |
1,193 |
5,9074 |
5,9079 |
|
1194 |
1,194 |
5,9101 |
5,9108 |
|
1195 |
1,195 |
5,9129 |
5,9136 |
|
1196 |
1,196 |
5,9156 |
5,9165 |
|
1197 |
1,197 |
5,9184 |
5,9194 |
|
1198 |
1,198 |
5,9212 |
5,9223 |
|
1199 |
1,199 |
5,9241 |
5,9252 |
|
1200 |
1,2 |
5,9241 |
5,9281 |
 –
минимальная сумма квадратов разностей.
–
минимальная сумма квадратов разностей.
Проверим ошибку многочлена степени 21:
m = 21.

 .
Ошибка также немного увеличилась по
сравнению с ошибкой, полученной нами
для степени 20. Порядок малости ошибки
не изменился.
.
Ошибка также немного увеличилась по
сравнению с ошибкой, полученной нами
для степени 20. Порядок малости ошибки
не изменился.
Подсчитаем ошибку для многочлена 19-й степени.
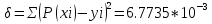 .
Ошибка на порядок выше, чем для степени
20.
.
Ошибка на порядок выше, чем для степени
20.
Оптимальным многочленом является P20(x).
График полученного многочлена приведен на рис.4. Как видим, он практически совпадает с графиком функции на [0.801,1.2]
 Рис.4
Рис.4
В точках разбиения функции высчитываем сглаживающие многочлены – полиномы 3-й степени.
Для отрезка [x1,x2] полином будет выглядеть так:

Коэффициенты полинома найдем из следующей системы:


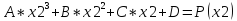


где – интерполяционный многочлен, выбранный
для данного отрезка.
– интерполяционный многочлен, выбранный
для данного отрезка.
На отрезке [0.4,0.401] получаем:





Получаем
многочлен

На отрезке [0.8,0.801] получаем:





Получаеммногочлен

Уточнение корней на интервале. ε = 0.0001
Как видно из графика, функция yпересекает ось Ox 4 раза, то есть имеет на интервале [0..1.2] 4 корня. Их удобно уточнять методом касательных, т.к. функция yне задана аналитически.
Пусть
 Тогда:
Тогда:
 гдеa,b
– верхняяинижняяграницыотрезка,
накоторомуточняетсякорень. Выбор
неподвижной границы (назовем ее с)
зависит от условия:
гдеa,b
– верхняяинижняяграницыотрезка,
накоторомуточняетсякорень. Выбор
неподвижной границы (назовем ее с)
зависит от условия:
 ,
при этом для всех приближений xi
выполняется условие:
,
при этом для всех приближений xi
выполняется условие:

1-й корень
уточняется на
 т.е.
т.е.
 (кривая вогнута), g(а)
=1.6539>0. Значит,
(кривая вогнута), g(а)
=1.6539>0. Значит,

|
i |
xi |
g(xi) |
|
0 |
0.1150 |
-7.9507 |
|
1 |
0.1026 |
-0.2053 |
|
2 |
0.1023 |
5.5753*10^-3 |
|
3 |
0.1023 |
|
x2=x3. На 2й итерации получаем x = 0.1023.
2й корень
уточняется на [0.205,0.207], т.е.
 (кривая выпуклая),
(кривая выпуклая),
 .
Значит,
.
Значит,

|
i |
xi |
g(xi) |
|
0 |
0.2070 |
0.3659 |
|
1 |
0.2065 |
0.1412 |
|
2 |
0.2063 |
0.0513 |
|
3 |
0.2062 |
6.2637*10^-3 |
|
4 |
0.2062 |
|
x3=x4. На 3-й итерации получаем x = 0.2062.
3й корень
уточняется на [0.38,0.4], т.е.
 (кривая выпуклая),
(кривая выпуклая),
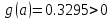 .
Значит,
.
Значит,

|
i |
xi |
g(xi) |
|
0 |
0.4000 |
-0.6179 |
|
1 |
0.3870 |
-0.2115 |
|
2 |
0.3843 |
-0.0299 |
|
3 |
0.3840 |
-7.5654*10^-3 |
|
4 |
0.3840 |
|
x3=x4. На 3-й итерации получаем x = 0.3840.
4й корень
уточняется на [0.417,0.42], т.е.
 (кривая выпукла),
(кривая выпукла),
 .
Значит,
.
Значит,

|
i |
xi |
g(xi) |
|
0 |
0.42 |
0.1325 |
|
1 |
0.4181 |
-6.6486*10^-4 |
|
2 |
0.4181 |
|
x1=x2. На 1-й же итерации получаем x = 0.4181.
