6. Примеры решения задач исследования операций

6.1. Общая постановка задачи

Линейного программирования

Дана система m линейных уравнений и неравенств с n переменными:

a₁₁ x₁ a₁₂ x₂ +…+a_1n x_n  b₁,

a₂₁ x₁ + a₂₂ x₂ +…+ a_2n x_n  b₂,

………………………………

a_k1 x₁ + a _k2 x₂+…+a _kn x _n  b _k,

a _k+1,1 x₁ + a _k+1,2 x₂ +…+ a _k+1,n x _n = b _k+1, (1)

a _k+2,1 x₁ + a _k+2,2 x² +…+ a _{k+2, n} x _n = b _k+2,

…………………………………………….

a _m1 x₁+a _m2 x₂+…+a _mn x_n = b_m,

или в краткой записи

и линейная (целевая) функция

F=c₁x+c₂x₂+…+с_n x_n. (2)

Необходимо найти такое решение системы (1)

X = (x₁, x₂, …, x_j, …, x_n),

где

x_j ≥ 0, (j=1, 2, …, l; l  n), (3)

при котором линейная функция (2) принимает оптимальное (т.е. максимальное или минимальное) значение.

Система (1) называется системой ограничений, функция (2) – линейной функцией, линейной формой, целевой функцией или функцией цели. Условия (3) носят название дополнительных условий.

Оптимальным решением (или оптимальным планом) задачи линейного программирования называется решение X=(x₁, x₂,…, x_n) системы ограничений (1), удовлетворяющее условию (3), при котором линейная функция (2) принимает экстремальное (максимальное или минимальное) значение.

При условии, что m>n, система ограничений (1) имеет множество решений. Решения задачи, удовлетворяющие системе (1) и дополнительным условиям (3), называются допустимыми. Рассмотрим два способа решения задачи.

6.2. Геометрический метод решения задачи линейного программирования

Этот метод основан на использовании теоремы:

Множество решений совместной системы m линейных неравенств с двумя переменными является выпуклым многоугольником (или выпуклой многоугольной областью). Оптимальное решение задачи линейного программирования располагается в одной из угловых точек многоугольника решений. Если линейная функция принимает экстремальное значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек, т.е. располагается на отрезке, соединяющем точки.

Многоугольник допустимых решений задачи может быть построен геометрическим методом (см. пример решения). Оптимальное решение выбирается либо путем перебора угловых точек, либо с использованием понятия линии уровня. Линией уровня линейной функции F называется линия, вдоль которой эта функция принимает одно и то же фиксированное значение F = a.

Пример.

Решить задачу линейного программирования геометрическим методом.

Условие задачи:

Система ограничений состоит из четырех неравенств с двумя переменными

x₁ + 3x₂  18,

2x₁ + x₂  16,

x₂  5, (4)

3x₁  21

Дополнительные условия задачи

x₁  0; x₂  0. (5)

Линейная функция имеет вид

F= 2x₁ +3x₂  max. (6)

Решение задачи:

1. Определим область допустимых решений задачи. Для этого последовательно рассмотрим каждое неравенство системы ограничений и дополнительные условия. В связи с тем, что каждое неравенство является нестрогим, (т.е.), уравнения, соответствующие им, являются их частными случаями. При этом каждому уравнению будет соответствовать прямая линия, построенная в координатных осях X₁, X₂. Для построения прямой необходимо иметь две точки. Например, для первого уравнения: x₁ + 3x₂ = 18. Первая точка: x₁ = 0, x₂ = 6. Вторая точка: x₁ = 18, x₂ = 0. Прямая, проведенная через эти точки, делит координатную плоскость на две полуплоскости. В одной из них лежат точки, удовлетворяющие неравенству системы ограничений, в другой – не удовлетворяющие ему. Для выбора нужной полуплоскости следует взять пробную точку в любой из полуплоскостей, например, x₁ = 0; x₂ = 0. Подставив координаты точки в первое неравенство системы ограничений, убедимся в том, что оно удовлетворяется. Отсюда следует, что все точки этой полуплоскости, включая точки прямой, удовлетворяют неравенству. Отбрасываем полуплоскость, лежащую выше и правее прямой 1. Поступая аналогично с остальными неравенствами системы ограничений, с учетом системы ограничений (5), получим многоугольник допустимых решений ОАБСДЕ (см. рис. 3). На рисунке он заштрихован. Координаты любой точки, лежащей внутри или на границе многоугольника, удовлетворяют системе ограничений (4) и дополнительным условиям (5).

2. Определим оптимальное решение задачи, т.е. выберем координату точки многоугольника, для которой целевая функция принимает максимальное значение. В соответствии с приведенной теоремой такой точкой является одна из угловых точек многоугольника.

Далее возможны два варианта действий:

а) перебрать все угловые точки многогранника допустимых решений, вычислить для них значения целевой функции и выбрать точку, обеспечивающую значение F_max;

б) воспользоваться линиями уровня для нахождения искомого решения.

Первый вариант не содержит принципиальных проблем. Для его использования необходимо определить координаты всех угловых точек многоугольника допустимых решений и подставить их в выражение целевой функции. Координаты точки, обеспечивающие получение максимального значения целевой функции, являются оптимальным решением задачи.

Использование линии уровня требует дополнительных пояснений. В рассматриваемой задаче уравнение линии уровня имеет вид

2x₁ + 3x₂ = a,

где параметр a может принимать любое значение.

Каждому значению параметра a соответствует своя линия уровня (для двух переменных это прямая линия). Наклон этих линий к координатным осям остается постоянным, т.к. коэффициенты при переменных неизменны при изменении значения параметра a . Таким образом, линии уровня образуют семейство параллельных прямых.

На рис. 3 показана линия уровня со значением параметра a=0, т.е. F=0. Эта прямая в соответствии с уравнением линии уровня проходит через начало координат. Линия уровня, отвечающая максимальному значению целевой функции F_max, должна находиться в контакте с одной из угловых точек области допустимых решений задачи и быть параллельной линии F=0 .

Расположение последней линии определят положение угловой точки многоугольника допустимых решений, составляющей оптимальное решение задачи. Это точка С с координатами x₁ = 6 x₂ = 4. Таким образом, оптимальным решением задачи будет Х* = (6; 4). Этому решению соответствует значение целевой функции F_max = 24.

14 1

4

8 3

А В

4 С

Д 2

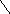
О 3 6 Е 9 12 15 18

F=0

Рис. 3. Определение оптимального решения задачи

В некоторых вариантах задача линейного программирования имеет множество оптимальных решений. Такая ситуация складывается, когда одна из прямых, ограничивающих область допустимых решений задачи, параллельна линии уровня. Формально это соответствует тому, что коэффициенты при переменных в одном из неравенств системы ограничений пропорциональны соответствующим коэффициентам в выражении целевой функции.