6. Пример математической постановки задачи

Пример математической постановки задачи приведен по теме «Оптимизация планирования поставки грузов» из реального курсового проекта.

Транспортные модели (задачи) — специальный класс задач линейного программирования. Эти модели часто описывают перемещение (перевозку) какого-либо товара из пункта отправления (исходный пункт, например место производства) в пункт назначения (склад, магазин, грузохранилище). Назначение транспортной задачи — определить объем перевозок из пунктов отправления в пункты назначения с минимальной суммарной стоимостью перевозок. При этом должны учитываться ограничения, налагаемые на объемы грузов, имеющихся в пунктах отправления (предложения), и ограничения, учитывающие потребность грузов в пунктах назначения (спрос). В транспортной модели предполагается, что стоимость перевозки по какому-либо маршруту прямо пропорциональна объему груза, перевозимого по этому маршруту. В общем случае транспортную модель можно применять для описания ситуаций, связанных с управлением запасами, управлением движением капиталов, составлением расписаний, назначением персонала и др.

Хотя транспортная задача может быть решена как обычная задача линейного программирования, ее специальная структура позволяет разработать алгоритм с упрощенными вычислениями, основанный на симплексных отношениях двойственности.

Дано: m пунктов отправления груза и объемы отправления по каждому пункту a1, a2, ..., a_m. В роли последних выступают объемы выпуска на каждом предприятии поставщика. Известна потребность в грузах b1, b2,...,b_n по каждому из n пунктов назначения. Потребности определяются из пришедших менеджеру по поставкам заявок, на поставку продукции от каждой из точек сбыта. Задана также С — матрица стоимостей доставки груза из пункта i в пункт j, с_ijC,(i=1,2,,...,m,j=1,2,...,n). Допустим, что с_ij- это цена бензина, затраченного на транспортировку продукции от поставщика потребителю.

В модели системы поставки продукции вместо матрицы стоимостей перевозок могут задаваться матрицы расстояний. В таком случае в качестве целевой функции рассматривается минимум суммарной транспортной работы.

Требуется получить: оптимальный план перевозок, т. е. определить, сколько груза x_ij  X должно быть отправлено из каждого пункта отправления (от поставщика) в каждый пункт назначения (до потребителя) с минимальными суммарными транспортными издержками. Естественно, чем меньше суммарный путь, тем меньше транспортные издержки.

Решение

Итак, входными параметрами системы являются m,n,A,B,C,

где m - количество поставщиков;

n - количество пунктов назначения;

А - множество, элементами которого являются объемы груза, отправляяемые из каждого пункта поставки;

В - множество, элементами которого являются объемы груза, необходимые в каждом пункте назначения; ;

С - множество стоимостей перевозок от каждого поставщика каждому потребителю..

Выходным параметром является множество X, элементами которого являются объемы груза, поставляемого от каждого поставщика каждому потребителю при минимальных транспортных издержках Z; .

Транспортная задача называется закрытой /22/, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения

.

Если такого равенства нет (потребности выше запасов или наоборот), задачу называют открытой.

Для написания математической постановки закрытой транспортной задачи необходимо все условия (ограничения) и целевую функцию представить в виде математических соотношений. Все грузы из i-х пунктов (поставщики) должны быть отправлены, т. е.:

.

Все j-е пункты (потребители) должны быть обеспечены грузами в плановом объеме:

.

Из логических соображений должно выполняться также условие неотрицательности переменных, так как количество груза не может быть отрицательным:

.

Перевозки необходимо осуществить с минимальными транспортными издержками (суммарной транспортной работой). Следовательно, целевая функция примет вид:

.

Таким образом, математическая формализация постановки транспортной задачи закрытого типа имеет следующий вид:

,

Как видно из выражения, уравнение баланса является обязательным условием решения закрытой транспортной задачи, поэтому, когда в исходных условиях дана открытая задача, ее необходимо привести к закрытой форме. Если:

• потребности по пунктам назначения превышают запасы пунктов отправления, то вводится фиктивный поставщик с недостающим объемом отправления;

• запасы поставщиков превышают потребности потребителей, то вводится фиктивный потребитель с необходимым объемом потребления.

Варианты, связывающие фиктивные пункты с реальными, имеют нулевые оценки. После введения фиктивных пунктов задача решается как закрытая.

В удобном для просмотра виде исходные данные представлены в табл. 2.

Таблица 2.

Потребители Поставщики	B1	B2		Bn	Запасы (объемы отправления)
А1	С11 X11	C12 X12	…	C1n X1n	a1
А2	С21 X21	C22 X22	…	C2n X2n	a2
	…	…	…	…	…
Аm	Сm1 Xm1	Cm2 Xm2	…	Cmn Xmn	am
Потребность	b1	b2	…	bn

Как уже было изложено, процесс оптимизации планирования поставки продукции состоит в решении транспортной задачи.

Наиболее лучшим для проектирования и распространенным методом решения транспортных задач является метод потенциалов, так как он предполагает итерационный процесс вычисления оптимального плана поставок и хорошо алгоритмизируется.

Потенциалы - вспомогательные переменные в транспортной задаче, вводимые для проверки оптимальности плана перевозок.

В первую очередь необходимо выполнить разработку начального плана (опорного решения).

Решение задачи методом потенциалов включает следующие этапы:

• расчет потенциалов;

• проверку плана на оптимальность (если план оптимальный, то вычислительный процесс прекращается, в противном случае выполняются следующие пункты);

• поиск максимального звена неоптимальности;

• составление контура перераспределения ресурсов;

• определение минимального элемента в контуре перераспределения;

• перераспределение ресурсов по контуру и возврат к первому этапу.

Описанная процедура повторяется несколько раз (итераций), пока не будет найдено оптимальное решение. Вычислительный алгоритм для каждой итерации не меняется.

Построение начального плана

Опорный план - план перевозок, у которого число ненулевых перевозок N равно сумме числа производителей и потребителей без единицы(N=m+n-1).

Для транспортной задачи существует несколько методов отыскания начального плана (опорного решения):

• метод северо-западного угла;

• метод минимальной стоимости по строке;

• метод двойного предпочтения и т. д.

Начальный план можно составить одним из перечисленных методов.

Воспользуемся способом минимальной стоимости по строке, так как он дает начальный план, наиболее приближенный к оптимальному. Суть метода заключается в том, что начиная с 1-й строки, в каждой строке выбирают клетку с наименьшей стоимостью и в нее помещают меньшее из чисел a_i и bj. Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку, и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Если у поставщика еще остались запасы, то из оставшейся части строки снова выбирают клетку с наименьшей стоимостью и в нее помещают меньшее из чисел a_i и bj. Далее переходят на следующую строку. Процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

Итак, математическая модель процесса построения начального плана методом минимальной стоимости по строке примет следующий вид:

Для i=1. .m выполнить:

ta_i=a_i.

Дляj=1..n выполнить:

tb_j=b_j.

jmin=1, j=1,c_min=c_1,1;

Для i=1..m выполнить:

Пока ta_i>0:

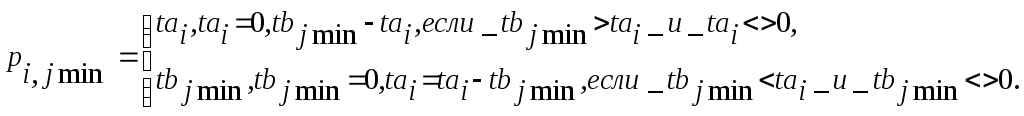
где j_min - j-координата элемента множества С с минимальной стоимостью транспортировки, j_min=1..n;

ta_i - объем запасов у i-го поставщика. ta -рабочее множество запасов поставщиков;

tb_j - объем потребностей у j-го потребителя. ta -рабочее множество потребностей потребителей;

c_min - минимальная стоимость транспортировки;

- количество груза, поставляемого от i-го поставщика j_min потребителю; p_i,jminP; P - рабочее множество объемов груза, поставляемого от поставщиков потребителям;

Введем функцию загр(h_i,j) для определения истинности загруженности элемента . Функция принимает истинное значение только в том случае, если элементу h_i,j ранее было присвоено какое либо значение. H - множество объемов перевозок от поставщиков потребителям.

.

Расчет потенциалов

В процессе решения после каждой итерации (в том числе и после получения допустимого решения) по загруженным клеткам проверяется выполнение следующего условия:

N=m+n-1,

где N - число загруженных клеток.

Если это условие не выполняется, план называется вырожденным и дальнейший расчет невозможен. Математически это можно представить так:

Для i=1. .m выполнить:

Для j = 1..n выполнить:

p_i,j = 0.

Для i=1. .m выполнить:

Для j=1..n выполнить:

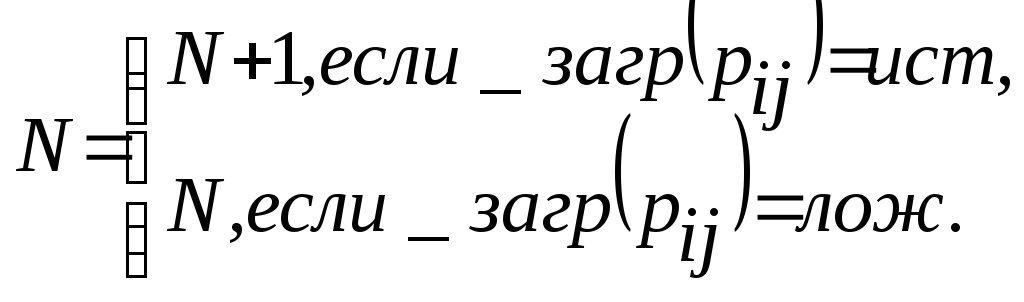
Если N<m+n-1, то дальнейшие вычисления невозможны, прекратить вычисления, где N - число загруженных клеток.

Потенциалы рассчитывают по загруженным клеткам, для которых должно выполняться следующее равенство:

,

где α_i - потенциал i-й строки, β_j - потенциал j-го столбца.

Вычисляя потенциалы, принимаем для первой строки α_i =0. Далее по загруженным клеткам определяем другие потенциалы. Математическая модель процесса определения потенциалов имеет вид:

Для i=1. .m выполнить:

alfa_i=0.

Для j = 1..n выполнить:

betta_j=0.

Для i=1. .m выполнить:

za_i=0,

Для j = 1..n выполнить:

zb_j=0.

alffa₁=0, za₁=1, k=1;

Выполнять:

Для i =1..m выполнить:

Для j =1..n выполнить:

Для i =1..m выполнить:

Для j =1..n выполнить:

Пока k<>m+n.

где alfa_i- потенциал i-й строки, alfa_iALFA; ALFA - множество строчных потенциалов;

betta_j - потенциал j-й строки, betta_jBETA; BETA - множество столбцовых потенциалов;

za_i - флаг, сигнализирующий о том, что у данной строки уже был рассчитан потенциал; za_iZA -множество флагов для строк;

zb_j - флаг, сигнализирующий о том, что у данного столбца уже был рассчитан потенциал; za_iZA - множество флагов для столбцов.

Проверка плана на оптимальность

Проверяем план на оптимальность по незагруженным клеткам, используя следующее неравенство:

.

Если для незагруженных клеток условие выполняется, то план - оптимальный. Математическая модель процесса проверки плана на оптимальность имеет вид:

КОН = ист.

Для i =1..m выполнить:

Для j =1..n выполнить:

Если КОН = ист., то x_i,j = p_i,j , прекратить вычисления.

здесь КОН- признак конца процесса вычисления, если КОН = = ист., значит, получен оптимальный план.

Поиск максимального звена неоптимальности

Максимальное звено неоптимальности находится как max() среди незагруженных клеток.

Эту клетку необходимо загрузить за счет перераспределения ресурсов из других загруженных клеток. Клетку в таблице помечаем знаком "+", так как здесь в начальном плане находится вершина максимальной неоптимальности.

Математическая модель данного процесса примет следующий вид:

iмзн = 1;

jмзн = 1;

МЗН=с₁₁.

Для i =1..m выполнить:

Дляj =1..n выполнить:

где jмзн, iмзн - j и i координаты максимального звена неоптимальности; МЗН- значение максимального звена неоптимальности.

Составление контура перераспределения ресурсов

Контур перераспределения ресурсов составляют по следующим правилам:

• этот контур представляет замкнутый многоугольник с вершинами в загруженных клетках, за исключением клетки с вершиной максимальной неоптимальности "+", и звеньями, лежащими вдоль строк и столбцов матрицы;

• ломаная линия должна быть связанной в том смысле, что из любой ее вершины можно попасть в любую другую вершину по звеньям ломаной цепи (по строке или по столбцу);

• в каждой вершине контура встречаются только два звена, одно из них располагается по строке, другое - по столбцу;

• число вершин контура четное, все они в процессе перераспределения делятся на загружаемые и разгружаемые;

• в каждой строке (столбце) имеются две вершины: одна - загружаемая, другая - разгружаемая.

Математическая модель данного процесса примет следующий вид:

Для i =1..m выполнить:

Дляj =1..n выполнить:

tp_i,j =p_i,j

Пока КНЦ = лож выполнять:

КНЦ = ист.;

Для i=1. .m выполнить:

Дляj=1..n выполнить:

k=1, ui₁ = iмнз, uj₁ =jмнз;

Выполнять:

k=k+1;

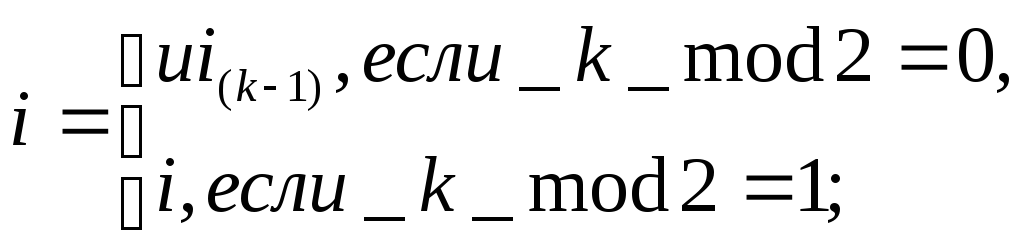
Для j=1..n выполнять:

Для i=1..m выполнять:

Пока ui_к = iмнз и uj_к =jмнз.

здесь КНЦ - флаг, сигнализирующий о том, что в таблице остались только вершины контура перераспределения ресурсов;

k - количество вершин в контуре + 1;

ui_к - i-координата k-й вершины контура; ui - множество i-координат вершин контура;

uj_к - j-координата k-й вершины контура; uj - множество j-координат вершин контура.

Введем функцию ВССЕ(i,j). Эта функция принимает истинное значение в том случае, если в i-й строке и вj-м столбце есть еще хотя бы одна загруженная клетка за исключением элемента с координатами i,j.

Определение минимального элемента в контуре перераспределения

Для получения оптимального плана необходимо перераспределить ресурсы по контуру. В процессе перераспределения ресурсов по контуру в соответствии с условием неотрицательности переменных х, ни одно из этих значений не должно превратиться в отрицательное число. Поэтому анализируют только разгружаемые клетки, из которых выбирают клетку с минимальным объемом перевозок (минимальный элемент в контуре).

Математическая модель данного процесса примет следующий вид:

МИНЭ =0.

Для i=1..k-1 выполнять:

где МИНЭ - значение минимального элемента в контуре.

Перераспределение ресурсов по контуру

Перераспределение ресурсов по контуру происходит очень просто: при движении по столбцу от имеющихся компонентов плана надо отнимать минимальный элемент в контуре, а при движении по строке наоборот прибавлять минимальный элемент в контуре.

Математическая модель данного процесса примет следующий вид:

Для i=1..k-1 выполнять:

Таким образом, математическая модель процесса оптимизации планирования поставки продукции создана. Данная модель адекватно описывает определение оптимального плана поставки на основе метода потенциалов. Также спроектирована математическая модель определения опорного плана на основе метода минимального элемента по строке.

Описание контрольного примера

Для описания контрольного примера возьмем процесс построения оптимального плана поставки продукции, выполняемый нашей программой, и проведем его вручную.

Фирма имеет 3 склад, на которых хранится картофель. С этой фирмой заключили договор на поставку картофеля 4 крупных магазина. Первому магазину необходимо 10 тонн картофеля, второму – 30т, третьему – 70т, четвертому – 30т. На первом складе фирмы хранится 20 тонн картофеля, на втором — 40 тонн, на третьем 80 тонн. Необходимо получать оптимальный план поставки картофеля потребителям. Также на основе статистических исследований известна стоимость доставки (в сот. руб.) из каждого склада в каждый магазин. Итак, мы имеем начальные данные, которые представлены в табл. 3.

Таблица 3.

Исходные данные

ПН ПО	В1	В2	В3	В4	Запасы аi
А1	4	2	4	3	20
А2	2	3	1	6	40
А3	3	4	5	2	80
Заявки bj	10	30	70	30	140

Методом минимальной стоимости по строке определяем начальный план (табл.4) и производим расчет потенциалов по загруженным клеткам(табл. 5).

Таблица 4.

Начальный план

ПН ПО	В1	В2	В3	В4	Запасы аi
А1	4	2 20	4	3	20
А2	2	3	1 40	6	40
А3	3 10	4 10	5 30	2 30	80
Заявки bj	10	30	70	30	140

Таблица 5.

Расчет потенциалов

ПН ПО	В1	В2	В3	В4
А1	4 с=1	2 20	4 с=3	3 с=0	0
А2	2 с=-1	3 с=0	1 40	6 с=-2	-2
А3	3 10	4 10	5 30	2 30	2
	1	2	3	0

Проверка плана на оптимальность по незагруженным клеткам.

План оптимальный, так как для всех незагруженных клеток выполняется .

Общие транспортные издержки:

Z = 360 сот. руб.

Итак, в результате построения плана поставки мы выяснили, что мы достигнем минимальных транспортных издержек в том случае, если:

Из 1-го склада доставим во 2-й магазин 20 тонн картофеля.

Из 2-го склада доставим 40 тонн в 3-й магазин.

Из 3-го склада доставим в 1-й магазин 10 тонн, во 2-й магазин 10 тонн, в 3-й магазин 30 тонн, в 4-й магазин 30 тонн. При этом общие транспортные издержки составят 360 сот. руб.

Данные контрольного примера должны быть сравнены с данными контрольного тестирования программы, образец приведен ниже.

Тестирование программы проводится на основе данных контрольного примера.

Зададим количество поставщиков и потребителей:

введите количество поставщиков (2<=Na<=5) 3

введите количество потребителей (2<=Nb<=5) 4

Зададим матрицу стоимостей доставки продукции от каждого поставщика каждому потребителю (рис. 4).

Рис. 4. Матрица стоимости продукции

В результате работы программы мы получаем оптимизированный план поставки продукции (рис. 5).

Рис. 5. Оптимизированный план поставки продукции.

Полученные нами в результате тестирования данные полностью совпадают с данными, полученными в контрольном примере, что свидетельствует о правильности функционирования ПО.