
Інтегр.числення_copy.pdf1
.pdf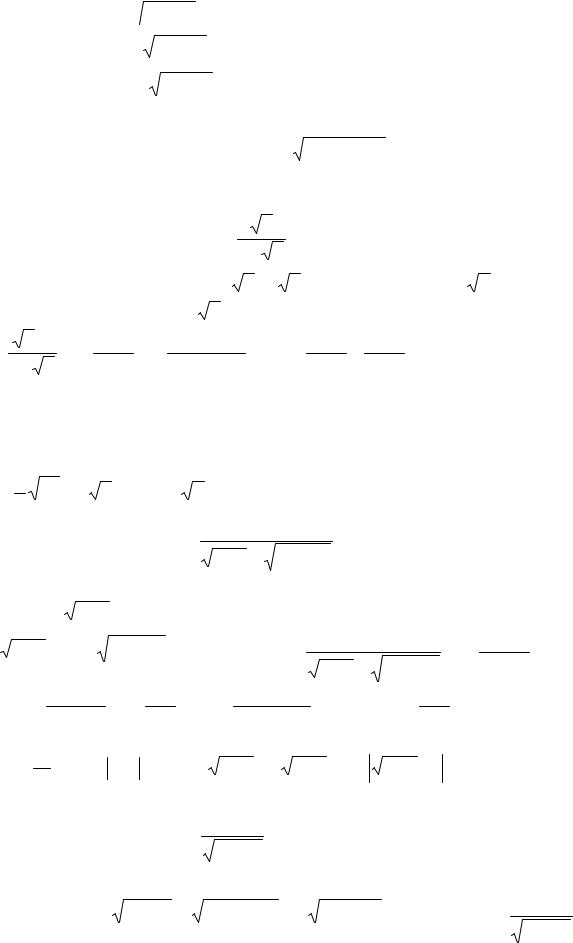
а) інтеграл ∫ R(x, a2 −x2 )dx знаходиться підстановкою x = asint ; x = a cos t ,
a2 −x2 )dx знаходиться підстановкою x = asint ; x = a cos t ,
б) інтеграл |
∫ R(x, |
x2 +a2 )dx |
знаходиться підстановкою x = atgt , |
|
||
в) інтеграл |
∫ R(x, |
x2 −a2 )dx |
знаходиться підстановкою x = |
a |
або |
|
sint |
||||||
x = acht. |
|
|
|
|
||
|
|
|
|
|
||
Зауваження. |
Інтеграли |
∫ R(x, ax2 +bx+c)dx зводяться до одного з |
||||
цих трьох інтегралів, якщо виділити повний квадрат в квадратному тричлені і основу його позначити через нову змінну інтегрування.
|
|
Приклад 1. |
|
|
Знайти |
|
|
∫ |
|
4 |
x |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1+ |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Розв'язування. Оскільки |
|
|
x = (4 x )2 , то ввівши заміну 4 x = t , дістане- |
||||||||||||||||||||||||||||||||||||||
мо |
x = t4 , |
dx=4t3dt |
і |
|
x = t2 . |
Тоді |
|
|
матимемо: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
∫ |
|
4 xdx |
|
= 4∫ |
t |
4dt |
=4∫ |
( t 4 −1) +1 |
|
t 4 −1 |
+ |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
dt = 4∫ |
|
2 |
|
|
2 |
|
dt = |
|
|
|
|
|
||||||||||||
|
1+ x |
|
|
1+ t |
|
|
|
|
t |
+1 |
|
|
|
|
|
+1 |
|
t |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
dt |
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
4∫ t |
|
|
|
− 1 + |
|
|
|
|
|
|
dt |
= 4 |
∫ t |
|
dt |
− ∫ dt + ∫ |
|
|
|
|
== 4 |
|
t |
|
|
− t + arctgt + C = |
|
|||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
t |
+ 1 |
|
|
|
|
|
|
|
|
|
|
t2 + 1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
4 4 |
|
x |
3 |
− 44 x + 4arctg4 x |
+ C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Приклад 2. Знайти ∫ |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x −1 + 3 (x −1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Розв′язування. Звівши обидва корані до кореня 6-го степення, введемо |
|||||||||||||||||||||||||||||||||||||||||
заміну |
|
|
6 x −1 = t , |
звідки |
|
х–1=t6, x=t6+1, |
dx=6t5 dt. Враховуючи те,що |
||||||||||||||||||||||||||||||||||||
|
|
x −1 = t3 , |
3 (x −1)2 |
= t 4 , дістанемо ∫ |
|
|
|
|
dx |
|
|
|
|
= 6∫ |
t |
3t5dt |
4 = |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
t 5dt |
|
|
|
|
|
|
|
t 2 |
|
|
|
|
|
|
(t 2 |
|
|
|
|
x −1 + 3 (x −1)2 |
|
|
+ t |
|
|
||||||||||
|
|
= 6∫ |
|
|
|
|
|
= 6∫ |
|
dt = 6∫ |
−1) |
+1 |
|
|
|
|
|
−1 |
+ |
|
|
1 |
|
= |
|
|
|||||||||||||||||
|
|
t |
3 (1 + t) |
t + |
1 |
|
t +1 |
|
dt = 6∫ t |
t |
+1 |
dt |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= |
|
|
2 |
|
− t + ln t +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6 t |
|
|
|
+ C = 33 x −1 − 66 x −1 + 6ln x −1 +1 + C |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Приклад 3. Знайти ∫ |
|
x2 dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
4 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Розв'язування. Виконавши заміну x=2sin t, будемо мати, що dx=2cost dt |
|||||||||||||||||||||||||||||||||||||||||
t=arcsin(x/2) і |
|
|
4 − x2 = |
|
4 − 4sin2t = 2 |
|
1 − sin2t = 2cost. Тоді ∫ |
x2 dx |
= |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
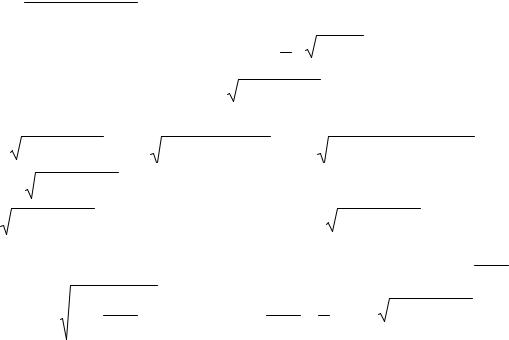
= ∫ |
4sin2t 2costdt |
= 4∫ sin2tdt = 2∫ (1− cos2t)dt = 2t − sin2t + C = |
|
||||||
|
2cost |
|
|
|
− 1 x |
|
|
|
|
= 2t − 2sintcost + C = 2arcsin(x / 2) |
|
4 − x2 + C. |
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
Приклад 4. |
Знайти |
∫ 3 + 2x − x2 dx. |
|
|||||
|
Розв′язання. Виділимо повний квадрат в квадратному тричлені |
||||||||
∫ 3 + 2x − x2 dx = ∫ − (x2 − 2x − 3)dx = ∫ − ((x2 − 2x +1) − 4)dx = |
|
||||||||
= ∫ |
4 − (x −1)2 dx. Зробимо заміну x −1 = 2sint => x = 2sint +1; dx = 2costdt; |
||||||||
4 − (x −1)2 dx = 2cost . Тоді матимемо: ∫ 3 + 2x − x2 dx = 4∫ cos2t dt = |
|||||||||
= 2∫ (1+ cos2t)dt = 2t + sin2t + C = 2t + 2sintcost + C = 2 arcsin x −1 |
+ |
||||||||
|
x −1 |
|
2 |
|
x −1 |
|
1 |
2 |
|
|
|
2 arcsin |
+ |
(x −1) 3 + 2x − x2 + C. |
|
||||
+ (x −1) 1− |
|
+ C = |
2 |
2 |
|
||||
|
2 |
|
|
|
|
|
|
||
19
2 ВИЗНАЧЕНИЙ ІНТЕГРАЛ
2.1 Приклади задач, що приводять до визначеного інтеграла
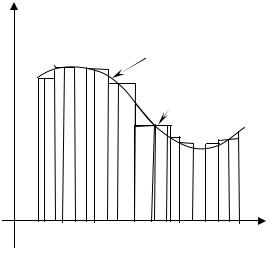
Задача 1 (задача про площу криволінійної трапеції). Знайти площу фігури, обмеженої зверху неперервною лінією, що є графіком функції y = f (x) , причому f (x) ≥ 0, двома прямими x = a і x = b та відрізком [a,b] числової осі Ох.
Задача 2 (задача проr роботу змінної сили). Знайти роботу, що
виконується змінною силою F , яка має постійний напрям, що збігається з віссю Ох , а точка прикладання переміщується з положення x = a в положення x = b , якщо величина сили змінюється за формулою F = f (x) ,
де f (x) – задана функція, визначена на [a,b].
Покажемо спосіб розв′язування першої задачі. Зробимо схематичний рисунок фігури.
y
y = f (x)
A
∆S1
Фігура аАВb називається криволі-
нійною трапецією. Площу цієї фігури не можна знайти засобами елементарної геометрії, бо в склад границі цієї фігури входить лінія АВ загального вигляду, що є
Bграфіком заданої неперервної функці f (x) .
Будемо поступати так:
|
|
|
|
|
|
|
x |
1. Розіб'ємо основу |
цієї |
фігури |
||
|
|
|
|
|
|
|
[a,b] довільним способом на n |
|||||
0 a ξ1x1ξ2x2x3 |
xi−1 ξi xi+1 |
xn−1 b |
||||||||||
x |
||||||||||||
|
|
|
|
|
|
|
|
частин точками x1, x2 , ... , xn−1 , |
||||
|
|
|
|
|
|
|
|
причому x1 < x2 < ... < xn−1 , |
тобто в |
|||
зростаючому порядку. |
Через |
x0 і |
xn |
позначимо кінці відрізка, тобто |
||||||||
x0 = a , |
xn =b. |
Отже, |
даний |
відрізок |
розбито на n малих відрізків |
|||||||
[x0 , x1],[x1, x2 ],...,[xn−1, xn ]. |
Довжини |
цих |
відрізків позначимо |
відповідно |
||||||||
через ∆ x1, ∆ x2 ,..., ∆ xn , |
|
|
|
|
|
|
|
|||||
тобто |
∆xi = xi |
– xi–1, де |
і = 1, 2,..., n. Далі через точки поділу xi проведемо |
|||||||||
прямі паралельно осі Оу до перетину з кривою АВ. Тоді криволінійна трапеція буде розбита на n малих елементарних трапецій, що не накладаються одна на одну. Тоді площа S криволінійної трапеції дорівнюватиме сумі площ цих малих трапецій, тобто S = ∆S1 + ∆S2 +…+ ∆Sn .
n
Отже, S = ∑ ∆Si , де через ∆Si позначено площу і-тої малої трапеції (∆Si ),
i =1
де і = 1, 2,..., n.
2. Виділимо і-ту малу трапецію і будемо визначати її площу наближено, замінивши цю малу трапецію прямокутником з тією ж
основою [xi −1 ,xi ] і висотою, що дорівнює значенню ординати кривої АВ в якійсь точці відрізка [xi −1 ,xi ]. Для цього на кожному з відрізків розбиття [xi−1 , xi ] виберемо довільно точку x = ξi , тобто ξi [xi−1,xi ], де i =1,2,...,n. Проведемо в кожній точці ξi паралельно осі Оу прямі до перетину з кривою АВ і визначимо ординати цих точок перетину, тобто yi = f (ξi ) ,
де i =1,2,...,n .
3. Кожну елементарну трапецію замінимо прямокутником, висота якого дорівнює саме цій ординаті, тобто hi = f (ξi ) , і визначимо площу кожного з цих прямокутників, яка дорівнюватиме f (ξi ) ∆xi , де i =1,2,...,n . Отже, площі елементарних трапецій наближено дорівнюватимуть цим
величинам, тобто ∆Si = f (ξi ) ∆xi , де і = 1, 2,..., |
n. |
4. Об’єднавши всі ці прямокутники, |
дістанемо так звану |
ступінчасту фігуру, яка покриває дану криволінійну трапецію. Площа цієї ступінчастої фігури дорівнюватиме сумі площ всіх цих прямокутників,
тобто Sст.ф. = f (ξ1)∆x1 + f (ξ2 )∆x2 + ... + f (ξn )∆xn |
або |
n |
|
Sст.ф. = ∑ f (ξi )∆xi . |
(*) |
i=1 |
|
Це число визначає наближене значення площі криволінійної трапе-
n
ції, тобто Sст.ф. ≈ ∑ f (ξi )∆xi .
i=1
5.Точне значення площі криволінійної трапеції дістанемо, якщо
згладити сходинки фігури, що можна зробити за умови, коли всі довжини [xi −1 ,xi ] прямують до нуля, а самі ці проміжки стягувати-
муться в точки. За означенням будемо вважати, що площа криволінійної
|
|
|
n |
|
|
|
трапеції |
дорівнює границі |
суми |
∑ f (ξi )∆xi |
за умови, |
що всі ∆xi → 0 , |
|
|
|
|
i =1 |
|
|
|
тобто |
S = |
lim |
∑n |
f (ξi )∆xi . |
(2.1) |
|
|
max ∆xi →0 i =1 |
|
|
|
||
2.2. Поняття визначеного інтеграла |
|
|
||||
Розглянемо функцію |
y = f (x) , |
визначену і неперервну на відрізку |
||||
[a,b] і для неї утворимо суми (*), виконавши вказані кроки. |
||||||
1. Розіб’ємо відрізок |
[a,b] |
довільним способом на п малих частин |
||||
точками |
х1 , х2 ,…, хп-1, де |
х1 < х2 <…< хп-1 , |
ввівши позначення х0 = а і |
|||
xn = b . |
Довжини цих малих відрізків [x0 ,x1 ], |
[x1 ,x2 ],..., |
[xn−1,xn ] позна- |
|||
чимо через ∆х1, ∆х2, ... , ∆хп, тобто ∆хi = xi − xi −1 , де i =1,2,...,n .
2.В кожному з цих малих відрізків розбиття [xi−1 ,xi ], де i =1,2,...,n , виберемо довільно точку ξі , тобто ξi [xi −1 ,xi ], і визначимо значення функції f (x) в цих точках, тобто знайдемо ƒ(ξ1), ƒ(ξ2) ,..., ƒ(ξп).
3.Утворимо добутки ƒ(ξ1)∆х1, ƒ(ξ2)∆х2 ,..., ƒ(ξп)∆хп .
4.Складемо суму цих добутків ƒ(ξ1)∆х1+ ƒ(ξ2)∆х2 +...+ƒ(ξп)∆хп або в
скороченому записі |
∑п |
f (ξi )∆xi . |
(2.2) |
||
|
|
і=1 |
|
|
|
Цю суму називають інтегральною сумою f (x) на відрізку [a,b]. |
|||||
В сумі (2.2) |
перейдемо до границі за умови, |
що ∆xi → 0 , а це |
|||
|
|
|
n |
|
|
викликає те, що n → ∞ , тобто |
lim |
∑ f (ξi )∆xi . |
|
||
|
|
max ∆xi →0 i =1 |
|
|
|
Означення. Якщо існує скінченна границя інтегральних сум за |
|||||
умови, що всі ∆xi |
→ 0 , яка не залежить від способу розбиття відрізку |
||||
[a, b] на частини , ні від вибору точок ξі в кожній частині розбиття, то цю |
|||||
границю називають визначеним інтегралом функції |
f (x) на проміжку |
||||
[a,b] і позначають символом |
b |
|
|
|
|
∫ f ( x)dx . |
|
|
|||
|
|
a |
|
|
|
Отже, |
b∫ f (x)dx = lim ∑n |
f (ξi )∆xi , |
(2.3) |
||
|
a |
λ →0 i=1 |
|
|
|
де λ – найбільша із довжин ∆хі , тобто λ = max ∆xi .
Числа a і b називають нижньою і верхньою межами інтегрування.
Якщо існує ця границя, то функція f (x) називається інтегровною
функцією на проміжку [a,b].
Виникає питання: а коли ж існує ця границя, відповідь на яке дає наступна теорема, яку тільки сформулюємо.
Теорема. Якщо функція f (x) неперервна на проміжку або має на
ньому скінченне число точок розриву першого роду, то на цьому проміжку функція інтегровна або визначений інтеграл існує.
Зауваження. Користуючись поняттям визначеного інтеграла, приведені дві задачі мають такі розв’язки:
b |
|
Skp.mp. = ∫ f (x)dx , |
(2.4) |
a
де f (x) − функція, графік якої обмежує криволінійну трапецію зверху, і
b |
|
r |
|
A = ∫ |
f (x)dx , де f (x) = |
F(x) |
. |
a |
|
|
|
Отже, геометрично визначений інтеграл чисельно дорівнює площі криволінійної трапеції.
2.3 Обчислення визначеного інтеграла
Оскільки визначений інтеграл – це границя, а границя – це число, то
як обчислити його. Безпосередньо, користуючись означенням, це зробити в |
|
загальному неможливо. Справедлива теорема. |
f (x) на відрізку [a,b] має |
Теорема. Якщо неперервна функція |
|
первісну F(x), то справедлива формула |
|
b |
|
∫ f (x)dx = F (b) − F (a) . |
(2.5) |
a |
|
Ця формула називається основною |
формулою інтегрального |
числення або формулою Ньютона – Лейбніца і встановлює зв’язок визначе-
ного інтеграла із невизначеним інтегралом.
Доведення. Оскільки функція f (x) неперервна на проміжку [a,b], то
b
її визначений інтеграл ∫ f ( x)dx існує, при цьому границя інтегральної
a
суми не залежить ні способу розбиття відрізку [a,b] на частини, ні від вибору точок ξi на них. Нехай F(x) є первісною для функції f (x) на відрізку [a,b], тобто F ′(x) = f (x) для всіх x [a,b], при цьому F(x) має неперервну похідну.
Розіб’ємо відрізок [a,b] довільним способом на п частин точками х1,
х2,..., xn−1 , причому x1 < x2 < ... < xn−1 , x0 = a і xn = b . Застосуємо формулу Лагранжа для функції F(x) на кожному із відрізків розбиття (умови теореми Лагранжа виконані, бо F(x) не тільки диференційовна на них, а має ще неперервну похідну). Матимемо такі рівності (з врахуванням того,
що F′(x) = f (x) ):
F(x1) − F(x0 ) = F′(c1) (x1 − x0 ) = f (c1)∆x1, де x0 < c1 < x1, F(x2 ) − F(x1) = F′(c2 ) (x2 − x1) = f (c2 )∆x2 , де x1 < c2 < x2 ,
F(x3) − F(x2 ) = F′(c3) (x3 − x2 ) = f (c3)∆x3 , де x2 < c3 < x3 ,…, F(xn ) − F(xn−1) = F′(cn ) (xn − xn−1) = f (cn )∆xn, де xn−1 < cn < xn .
Складемо суму лівих і правих частин цих рівностей, враховуючи те, що в лівій частині після знищення відповідних пар дістанемо F(xn ) − F(x0 ) ,
|
|
n |
n |
|
матимемо F (xn ) − F (x0 ) = ∑ f (ci ) або |
∑ f (ci )∆xi = F (b) − F (a) , |
бо |
||
xn = b , |
|
i =1 |
i =1 |
|
x0 = a . В лівій частині записаної рівності стоїть інтегральна сума |
||||
функції |
f (x) |
на відрізку [a,b], де замість точок ξi взято точки ci , які |
||
визначаються |
формулою Лагранжа (ci належить відрізкам розбиття). |
В |
||
правій частині рівності стоїть стала величина. Перейдемо в останній
рівності до границі за |
умови, що всі ∆xi → 0 , матимемо |
n |
b |
lim ∑ f (ci )∆xi = F (b)− F(a) |
або ∫ f (x)dx = F(b) − F(a) , оскільки ця |
λ →0 i =1 |
a |
границя не залежить від вибору точок на кожному відрізку розбиття, і за
означенням є визначеним інтегралом функції |
|
f (x) . Теорему доведено. |
||
|
Зауваження. Формулу Ньютона – Лейбніца записують символічно |
|||
|
b |
|
b . |
|
так: |
∫ f (x)dx = F(x) |
|
(2.6) |
|
|
a |
|
a |
|
|
|
|
||
|
|
|
|
|
Приведемо приклади на обчислення визначеного інтеграла.
1) |
2 dx |
= ln | x | |
|
|
2 |
= ln 2 − ln1 = ln 2. |
|
|
||||||
|
|
|
||||||||||||
∫ |
x |
|
|
1 |
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
π |
|
|
|
|
|
|
|
|
|
π = − cosπ + cos 0 = 1+1 = 2. |
|
||
2) |
∫ sin xdx = − cos x |
|
|
|
||||||||||
|
|
|
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.4 Властивості визначеного інтеграла |
|
|||||||||||||
Ці властивості сформулюємо у вигляді теорем. |
|
|||||||||||||
Теорема 1. Сталий множник можна виносити за знак визначеного |
||||||||||||||
|
|
b |
|
|
|
|
|
b |
|
|
|
|||
інтеграла, тобто ∫Cf (x)dx = C ∫ f (x)dx. |
|
|
|
|||||||||||
|
|
a |
|
|
|
|
|
a |
|
|
|
|||
|
|
b |
|
|
|
|
|
|
n |
|
n |
|
||
Дійсно, ∫Cf (x)dx = lim ∑Cf (ξi )∆xi |
= lim (C |
∑ f (ξi )∆xi ) = |
|
|||||||||||
|
|
a |
|
b |
λ→0 i |
=1 |
λ→0 |
i=1 |
|
|||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= C lim ∑ f (ξi )∆xi =C∫ f (x)dx . |
|
|
|
|
|
|
||||||||
λ→0 i=1 |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
Теорема 2. Визначений інтеграл суми інтегровних на відрізку [a,b] |
||||||||||||||
функцій дорівнює сумі визначених інтегралів цих функцій, тобто |
|
|||||||||||||
b |
|
|
|
b |
|
|
|
|
b |
|
|
|
||
∫( f1(x) + f2 (x))dx = ∫ f1(x)dx + ∫ f2 (x)dx. |
|
|
|
|||||||||||
a |
|
|
|
a |
|
|
|
|
a |
|
|
|
||
Дійсно, за означенням |
|
|
|
|
|
|
||||||||
b |
|
|
|
|
n |
|
|
|
|
|
n |
n |
||
∫( f1(x) + f2 (x))dx = |
lim ∑( f1(ξi ) + f2 (ξi ))∆xi = |
lim (∑ f1(ξi )∆xi |
+ ∑ f2 (ξi )∆xi ) = |
|||||||||||
a |
|
|
|
λ→0 i=1 |
|
|
|
|
|
λ→0 i=1 |
i=1 |
|||
n |
|
|
|
|
n |
|
|
|
b |
|
b |
|
||
= lim ∑ f1(ξi )∆xi + |
lim |
∑ f2 (ξi )∆xi = ∫ f1(x)dx + ∫ f2 (x)dx. |
|
|||||||||||
λ→0 i=1 |
|
|
|
λ→0 i=1 |
|
|
|
a |
|
a |
|
|||
З цих двох властивостей випливає наслідок. Наслідок. Справедлива рівність
b |
b |
b |
|
∫(C1 f1(x)C2 f2 (x))dx = C1 ∫ f1(x)dx + C2 ∫ f2 (x)dx, |
(2.7) |
||
a |
a |
a |
|
де С1 і С2 – задані числа.
Ця властивість називається властивістю лінійності визначеного інтеграла.
Теорема 3. Для будь-якої точки x=c має місце рівність
b |
c |
b |
|
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx |
(2.8) |
||
a |
a |
c |
|
за умови, що функція f(x) інтегровна на найбільшому із цих трьох відрізків. Цю властивість називають властивістю адитивності визначеного
інтеграла.
Дійсно, нехай функція f(x) має первісну F(x) на найбільшому із цих двох відрізків. Тоді за формулою Ньютона – Лейбніца матимемо, що b
∫ f (x)dx = F(b) − F(a). Знайдемо тепер праву частину цієї рівності a
cb
∫ f (x)dx + ∫ f (x)dx = F (c) − F (a) + F(b) − F (c) = F(b) − F (a). Отже, обидві
ac
частини рівності однакові.
Теорема 4. Якщо функція f(x) інтегровна на відрізку [a,b], то
|
b |
a |
|
справедлива рівність |
∫ f (x)dx = −∫ f (x)dx. |
(2.10) |
|
|
a |
b |
|
Отже, при зміні меж інтегрування змінюється лише знак у визначеного інтеграла. Це очевидно, бо всі ∆xi поміняють знак.
|
Теорема 5. Справедлива рівність |
b |
|
|
|
|||
|
∫ dx = b − a. |
(2.11) |
||||||
|
|
|
|
|
a |
|
|
|
|
Дійсно, оскільки функція f (x) ≡ 1 при всіх x [a,b], то всі значення |
|||||||
f (ξi ) = 1, |
тоді |
|
|
|
|
|
|
|
b |
|
n |
n |
|
n |
|
|
|
∫ dx = |
lim |
∑ f (ξi )∆xi = lim ∑1 ∆xi = |
lim |
∑∆xi = lim (b |
− a) = b − a , бо |
|||
a |
λ→0 i=1 |
λ→0 i=1 |
λ→0 i=1 |
λ→0 |
|
|||
сума довжин ∆xi |
відрізків розбиття дорівнює довжині всього відрізка [a,b], |
|||||||
тобто числу b − a. |
|
|
|
|
|
|||
|
Теорема |
6. Якщо інтегровна |
функція |
f(x) |
при |
всіх значеннях |
||
x [a,b] приймає невід’ємні значення, тобто f (x) ≥ 0 |
|
b |
||||||
, то ∫ f (x)dx > 0. |
||||||||
a
|
Дійсно, нехай |
f (x) ≥ 0 |
при всіх x [a,b], то всі |
f (ξi ) ≥ 0. Оскільки |
||||
b>a, |
то |
всі |
∆xi > 0, |
тоді всі |
доданки |
f (ξi )∆xi інтегральної суми |
теж |
|
невід’ємні і принаймні один |
із них є додатним, тоді інтегральна сума |
|||||||
n |
|
|
|
|
|
n |
b |
|
∑ f (ξi )∆xi > 0 , звідки випливає, що lim |
∑ f (ξi ) > 0 , тобто ∫ f (x)dx > 0. |
|||||||
i=1 |
|
|
|
|
λ→0 i=1 |
a |
|
|
|
Теорема 7. Якщо для інтегровних на відрізку [a,b] функцій f(x) і |
|||||||
g(x) |
в |
усіх |
його |
точках |
виконується нерівність |
f (x) ≥ g(x) , |
то |
|
bb
∫ f (x)dx > ∫ g(x)dx. Довести самостійно.
aa
Вбагатьох питаннях теорії і практики доводиться користуватися
такими двома важливими теоремами.
Теорема 8 (теорема про оцінку визначеного інтеграла).
Якщо функція f(x) інтегровна на відрізку [a,b], а m і M відповідно її найменше і найбільше значення, то справедливі нерівності
b |
|
m(b − a) ≤ ∫ f (x)dx ≤ M (b − a). |
(2.12) |
a
Доведення. За визначенням найменшого і найбільшого значень функції для всіх x [a,b] виконується подвійна нерівність m ≤ f (x) ≤ M .
b |
b |
b |
Тоді за теоремою 7 і формулою (2.11) матимемо ∫ mdx ≤ ∫ f (x)dx ≤ ∫ Mdx ,
|
|
|
a |
a |
a |
b |
b |
b |
b |
|
|
m∫ dx ≤ ∫ f (x)dx ≤ M ∫ dx |
m(b − a) ≤ ∫ f (x)dx ≤ M (b − a), |
що треба |
|||
a |
a |
a |
a |
|
|
було довести.
Теорема 9 (теорема про середнє). Якщо функція f(x) неперервна на відрізку [a,b], то існує принаймні одна точка с [a,b] така, що виконується рівність
|
b |
|
|
|
|
|
|
∫ f (x)dx = f (c) (b − a). |
|
(2.13) |
|||
|
a |
|
|
|
|
|
Число f (c) називається середнім значенням функції на відрізку [a,b] . |
||||||
Доведення. Оскільки функція f (x) неперервна |
на відрізку [a,b], то |
|||||
вона має первісну |
F(x) , де |
F |
′ |
|
|
|
(x) = f (x) . Тоді за формулою Ньютона – |
||||||
|
|
b |
|
|
|
|
Лейбніца маємо, |
що |
∫ f (x)dx = F (b) −F(a) . За формулою |
Лагранжа |
|||
′ |
|
a |
|
a < c < b. (умови |
|
|
|
, |
де |
теореми |
Лагранжа |
||
F(b) − F(a) = F (c)(b − a) |
||||||

|
b |
|
|
виконані). Отже, |
′ |
|
|
∫ f (x)dx = F (c) (b − a) = f (c) (b − a) , де a < c < b. |
|||
Теорему доведено. |
a |
|
|
|
|
|
|
2.5 Інтеграл із змінною верхньою межею |
|
||
Нехай на відрізку [a,b], функція f (x) |
b |
|
|
інтегровною, тобто ∫ f (x)dx |
|||
існує. Виберемо тепер довільну точку x [a;b] |
a |
[a; x], |
|
і розглянемо відрізок |
|||
x
тоді існує ∫ f (t)dt . Оскільки кожному значенню x [a;b] відповідає певне
a
x
значення інтеграла ∫ f (t)dt , то ця величина є функцією змінною х (за
a
значенням функції). Отже, із змінною верхньою межею є функція цієї x
верхньої межі, тобто ∫ f (t)dt = I (x) .
a
Справедлива така теорема.
Теорема. Похідна визначеного інтегралу із змінною верхньою межею по цій верхній межі дорівнює підінтегральній функції в її верхній межі, тобто
x |
′ |
|
|
|
(∫ |
= f (x) . |
(2.13) |
||
f (t)dt) |
a
Дійсно, нехай F (x) є деяка первісна інтегровної функції f (x) , то за
x
формулою Ньютона – Лейбніца матимемо, що I (x) = ∫ f (t)dt = F(x) − F(a) ,
звідки |
маємо |
що |
|
I |
′ |
|
(F(x) − F |
|
′ |
′ |
a |
′ |
|
|||||||||
|
|
|
|
|
||||||||||||||||||
|
(x) = |
(a)) = F (x) |
− 0 = F (x) = f (x) . Отже, |
|||||||||||||||||||
|
|
b |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
∫ f (t)dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= |
= f (x) |
, що треба було довести. |
|
|
|
||||||||||||||||
I (x) |
|
|
|
|||||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
Приклад. Знайти похідну функцію φ(x) = |
∫e |
2 dt . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язування. Ця функція називається функцією Лапласа або |
||||||||||||||||||||
інтегралом |
ймовірностей. |
Користуючись |
формулою |
(2.13), дістанемо |
||||||||||||||||||
|
1 |
x |
−t 2 |
|
′ |
1 |
x |
− |
t 2 |
′ |
|
1 |
|
− |
x2 |
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
∫e |
dt |
|
|
∫e |
2 |
|
= |
e |
2 |
. |
|
|
|
|
|||||||
|
2π |
|
= |
2π |
|
|
|
dt |
2π |
|
|
|
|
|
|
|||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2.6 Метод заміни змінної інтегрування
