Інтегр.числення_copy.pdf1

Розглянемо питання, як метод підстановки використовується у визначеному інтегралі, в чому особливість цього методу. Справедлива така теорема.

Теорема. Якщо функція f (x) неперервна на відрізку [a,b], а функція x = ϕ(t) задовольняє такі умови:

1)		′
	функція ϕ(x) і її похідна ϕ (x) неперервні на деякому проміжку
	[α; β ];
2)	при зміні t від α до β	всі її значення однозначно попадають на
	відрізок [a,b], причому кожне значення x із відрізку		[a,b] є
	значенням функції ϕ(t) лише для одного із значень t на проміжку
	[α; β ] ;
3)	ϕ(α ) = a , ϕ(β ) = b ,то справедлива рівність
	b	β
		′	(2.14)
	∫ f (x)dx = ∫ f (ϕ(t))ϕ (t)dt .
	a	α

Доведення .Доведемо, що обидві частини рівні. З умов теореми випливає ,що обидва ці інтеграли існують. Нехай F(x) – первісна для f(x),

′	x [a;b]. Тоді за формулою
тобто F (x) = f (x) для всіх
b

Ньютона – Лейбніца маємо ∫ f (x)dx = F (b) −F(a) . З другого боку функція

			a		′	на проміжку [α; β ], бо
	F (ϕ(t)) буде первісною для функції
					f (ϕ(t))ϕ (t)
	′	′	′	′		знов	за формулою
	(F(ϕ(t)))	= F (ϕ(t)) ϕ (t) = f (ϕ(t)) ϕ			(t). Тоді
	Ньютона	–	Лейбніца		будемо		мати,	що
	β	′		= F (b) − F(a) .		Отож,	значення	лівої і
	∫ f (ϕ(t))ϕ (t)dt = F (ϕ(β )) − F (ϕ(α ))

α

правої частин рівняння збіглися.

Зауваження. Важливою особливістю метода підстановки є те , що не має необхідності повертатися до старої змінної інтегрування. Замість цього треба визначити межі інтегрування нової змінної.

a

Приклад. Знайти інтеграл ∫ a2 − x2 dx , де a > 0.

0

Розв'язування. Використаємо					підстановку	x = a sint		, звідки
dx = a costdt,		при	цьому		підінтегральна			функція
a2 − x2 =	a2 − a2sin2t = a		1 − sin2t = asint. Знайдемо межі інтегрування
нової змінної		t : при x = 0 asint = 0;			sint = 0 , звідки		t = πn; n Z;		при
x = a asint = a; sint = 1;			t = π	+ 2πn, n Z . При		зміні	t в	межах	від
	π		2
α = 0 до β =		функція x = asint		один раз приймає значення, що належать
	2

проміжку [0,a]. Це і є межі інтегрування нової змінної t . Тоді за формулою (2.14) матимемо

		π		π			π
a	a2 − x2 dx =	2	acost acostdt = a2	2	cos2tdt =	a2	2	(1	+ cos2t)dt =
∫		∫		∫		2	∫
0		0		0			0

ππ

=a2 ( 2∫ dt + 2∫ cos2tdt) = a2 (π + 0) = π a2 . 2 0 0 2 2 4

Відповідь: π 4a2 .

2.7 Метод інтегрування частинами

Вияснимо особливості цього методу для визначеного інтеграла.

Має місце теорема.
Теорема. Якщо функції u(x) і			v(x) мають неперервні	похідні
на відрізку [a,b], то справедлива рівність
b		b	b
∫ udv = uv		a	−∫ vdu.	(2.15)
a			a

Доведення. Скористаємось тим, що d (uv) = udv + vdu = u v' dx + v u' dx ,

звідки u(x)v' (x)dx = (u(x)v(x))′ dx−v(x) u' (x)dx. Проінтегруємо цю рівність

на відрізку [a,b], користуючись властивістю лінійності (всі інтеграли існують за вказаними умовами), будемо мати

b		b	b	b	b
∫ u(x)v' (x)dx	=	∫ (u(x)v(x))' dx −∫ v(x) u' (x)dx = u(x)v(x)		a	− ∫ v(x) u' (x)dx.
a		a	a		a
	b		b b
Отже, маємо ∫ udv = uv			− ∫ vdu , що треба було довести.

aa a

Зауваження. Хоч формула (2.15) має такий же вигляд, як і для невизначеного інтеграла, але є принципово простішою, бо це рівність між числами, а не функціями.

e

Приклад 1. Обчислити ∫ ln xdx.

1
Розв’язування. Приймемо u=lnx, dv=dx, то du =	1	dx, v = x, тоді
	x

e

e

e

1

e

∫ ln xdx = x ln x

−∫ x

dx

= e ln e

− ∫ dx = e

− (e − 1) = 1.

1

1

1

x

1

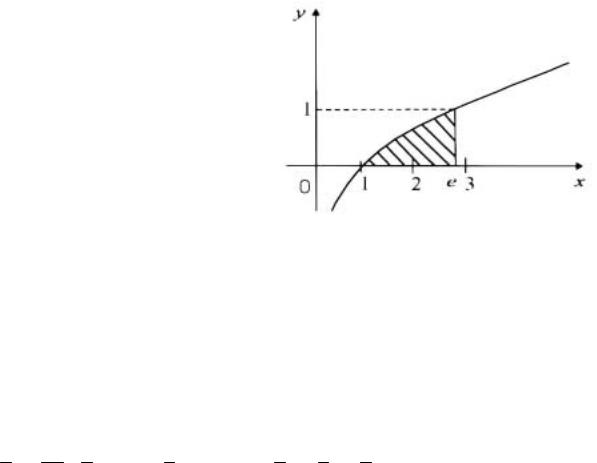
Зробимо схематичний рисунок.

Геометрично це означає, що

площа

криволінійної трапеції,

що обмежена

графіком функції

y=lnx, віссю

Ox та прямою x=e,

чисельно

дорівнює

одній

умовній

одиниці площі.

π

Приклад

2.

Обчислити

∫2

(2x − 3) cos 3xdx.

0

Розв’язування. Приймемо за u і dv відповідно u = 2x−3,

dv = cos 3xdx ,

π

то du = 2dx , v = ∫cos 3xdx =

1

∫cos 3xd(3x) =

1

sin3x , тоді

∫2

(2x − 3) cos 3xdx =

3

3

0

π

π

π

1 (2x − 3)sin3x

− 2

2

(π − 3)sin

3π

+ 4 cos 3x

= − 1

(π − 3) +

=

2

∫ sin3xdx = 1

2

3

0

3

0

3

2

9

0

3

+94 cos 32π − 94 cos 0 = − 13(π − 3 ) + 0 − 94 = − 13π + 95 .

2.8Невласні інтеграли

b

Поняття визначеного інтеграла ∫ f (x)dx вводиться за умови, що

a

проміжок інтегрування скінченний, а функція на ньому обмежена. Узагальнимо це поняття на випадки, коли: 1) проміжок інтегрування нескінченний, а функція на ньому неперервна або обмежена і 2) проміжок інтегрування скінченний, а функція лише в одній із його точок має необмежений розрив, тобто в деякому околі однієї із його точок є нескінченно великою.

2.8.1 Невласні інтеграли з безмежними межами інтегрування

1. Нехай функція f (x) визначена і неперервна на проміжку [a,+ ∞ ] Введемо довільну точку x=b на цьому проміжку і розглянемо відрізок[a,b],

на якому функція f (x) неперервна, тоді існує визначений інтеграл

b

∫ f (x)dx . Якщо верхню межу змінювати, то цей інтеграл буде функцією

a

b

своєї верхньої межі b, тобто ∫ f (x)dx = I (b) .

a

Відрізок [a,b] розтягнеться в проміжок [a, + ∞ ) за умови, що b→+ ∞ . Може статися, що за цієї умови функція I(b) має скінченну границю.

Означення. Якщо існує скінченна границя визначеного інтаграла

b

∫ f (x)dx за умови, що b→+ ∞ , то цю границю називають невласним

a

інтегралом функції f(x) на прпоміжку [a, + ∞ ) і позначають символом

∞

∫ f (x)dx . Отже,

a

∞

∫ f (x)dx =

a

	b
lim	∫ f (x)dx.	(2.16)
b→+∞ a

В цьому випадку говорять, що невласний інтеграл існує і називається

b

збіжним, якщо ж ∫ f (x)dx при b→+ ∞ не має границі, то невласний

a

інтеграл називається розбіжним.

Приведемо ряд прикладів. Обчислити або встановити розбіжність невласних інтегралів.

Приклад 1.

∞

dx

.

∫

1+ x2

1

∞

dx

b

dx

b

Розв’язування. За означенням ∫

=

lim ∫

= lim

2

2

1

+ x

1 + x

arctgx

=

1

b→+∞ 1

b→+∞

1

= lim (arctgb − arctg1) = lim arctgb − π

=

π

− π =

π . Цей невласний інтег-

b→+∞

b→+∞

4

2

4

4

рал є збіжним.

Зробимо

ще

схематичний

рисунок.

Геометрично

цей

інтеграл означає, що площа

безмежної

заштрихованої

фігури дорівнює

π

умовних

одиниць.

4

∞ dx

Приклад 2.

.

∫

1

x

	∞ dx			b dx
Розв’язування. За означенням	∫		= lim	∫		=	lim		x
		x			x
	1		b→+∞ 1				b→+∞

= lim (lnb − ln1) = ∞ . Отже, цей невласний інтеграл розбіжний.

b→+∞

b

=

1

∞

Приклад 3.

∫ xe−4x2 dx.

0

∞

b

Розв’язування. За означенням ∫ xe−4x2 dx =

lim

∫ xe−4x2

=

0

b→+∞

0

1

b

−4x

2

2

1

−4x

2

b

1

−4b

2

1

∫ e

d(−4x

e

e

= lim

−

) =

lim

−

=

lim −

+

=

8

8

8

b→+∞

0

b→+∞

0

b→+∞

8

=0+

1

=

1

.

8

8

Приклад 4. Встановити,

за яких умов невласний інтеграл

∞ dx

,

∫

де р − задане, буде збіжним, а за яких − розбіжним.

1 x p

x− p+1

∞ dx

b dx

b

Розв’язування. За означенням ∫

p

= lim

∫

p = lim

=

− p+1

1 x

b→+∞ 1 x

b→+∞ − p +1

1

= lim

b

−

1

.

1)

Якщо р>1, то

lim b− p+1 =

0, тому

∞

dx

=

1

,

∫

1− p

− p +1

p − 1

b→+∞

∞ dx

b→+∞

1 x p

Якщо р≤ 1, то при b→+ ∞

тобто невласний інтеграл ∫

− збіжний. 2)

x p

1

функція b− p+1 є нескінченно великою величиною,

тому вказана

границя

дорівнює нескінченності, а невласний інтеграл є розбіжним.

Отже,

невласний

інтеграл

∞ dx

при

р>1

збіжний,

а

при р≤ 1

∫

x p

1

розбіжний. Це важливий невласний інтеграл.

Зауваження 1. Аналогічно визначається невласний інтеграл з

безмежною нижньою межею інтегрування, а саме: за означенням

b

b

∫ f (x)dx =

lim

∫ f (x)dx.

(2.17)

−∞

a→−∞ a

Зауваження 2. Можна ввести невласний інтеграл для функції

f (x) ,

визначеної і неперервної на всій числовій прямій, а саме: за означенням

∞

c

∞

∫ f (x)dx =

∫ f (x)dx +

∫ f (x)dx ,

(2.18)

−∞

−∞

c

де с − довільно вибране число, часто беруть с = 0.

Якщо один із цих двох невласних інтегралів правої частини рівності

∞

розбіжний, то вважається, що невласний інтеграл ∫ f (x)dx розбіжний.

−∞

∞

Невласний інтеграл ∫ f (x)dx називається збіжним, якщо обидва невласні

−∞

інтеграли правої частини є збіжні.

2.8.2 Ознаки збіжності невласних інтегралів

Для розв′язування багатьох задач достатньо лише оцінити збіжність

невласного інтеграла, тобто достатньо встановити збіжність або розбіжність невласного інтеграла, не обчисляючи сам невласний інтеграл.Встановимо достатні ознаки збіжності невласних інтегралів.

Справедливі такі теореми.

Теорема 1. Якщо функція f (x) ≥ 0 при всіх x [a, + ∞ ) і при b → ∞

b
виконується нерівність ∫ f (x)dx ≤ М,	де М − деяке додатне число, то
a	∞
невласний інтеграл існує; і обернено,	якщо невласний інтеграл ∫ f (x)dx
	a

від невід′ємної функції f (x) є збіжним, то існує додатне число М таке, що

	b
виконується нерівність	∫ f (x)dx ≤ М за умови, що b → +∞ .
	a
Теорема 2. Якщо для двох невід′ємних функцій f (x)			і g(x) при всіх
x [а,+ ∞ ) виконується нерівність		f (x) ≤ g(x) , то із збіжності невласного
∞		∞
інтеграла ∫ g(x)dx	випливає	збіжність ∫ f (x)dx ;	із розбіжності
a		a	∞
∞
невласного інтеграла ∫	f (x)dx випливає розбіжність інтеграла ∫ g(x)dx .
a			a

Доведення. Доведемо спочатку першу частину теореми.

∞

Нехай ∫ g(x)dx збіжний, тоді за теоремою 1 знайдеться додатне число

a
b		що b
М таке, що ∫ g(x)dx ≤	М за умови,		→ +∞ .	Оскільки при всіх
a		f (x) ≤	g(x) ,
x [а,+ ∞ ) виконується	нерівність			то за властивістю
	b		b
визначеного інтеграла випливає, що ∫ f (x)dx ≤			∫ g(x)dx . Тоді при b → +∞
	a		a

				b
матимемо,			що	∫ f (x)dx ≤		М, а	тоді	за другою	частиною	теореми 1
			+∞	a
				f (x)dx є збіжним.
випливає, що ∫
			a
	Друга частина теореми доводиться методом від супротивного.
Зауваження. На практиці зручною є така форма цієї теореми:
	Якщо		функції		f (x)	і g(x)	невід’ємні на [a,+∞) і існує				границя
lim	f (x)	= k ≠ 0 , то			обидва невласні			інтеграли	+∫∞f (x)dx	і	∞∫ g(x)dx
x→∞ g(x)									a		a

одночасно збіжні або розбіжні.

lim

x→+∞

=p

∞

dx

Приклад 1. Дослідити на збіжність невласний інтеграл ∫

.

1

3 x 2 + 1

Розв’язування. Розглянемо функцію g(x)=

1

, оскільки

lim

f (x)

=

3

x

2

x→+∞ g(x)

1

3 x2

+1 = lim

3

x

2

∞

dx — розбіжний

=1≠ 0, і невласний інтеграл ∫

3

1

x→+∞3

x

2

+1

1

x

2

3 x2

∞

2

dx

<

1 , то і даний невласний інтеграл ∫

розбіжний.

3

3

2

1

x

+ 1

∞

Приклад 2. Оцінити збіжність невласного інтеграла ∫ e−x2 dx .

1

∞

Оскільки e−x2 < e−x для

Розв’язування.

всіх x [1,+∞) і ∫ e−x dx

1

∞

b

− e−x

b

lim (− e−b + e−1 )=

1

збіжний, бо ∫ e−x dx = lim

∫ e−x dx =

lim

=

,

e

1

b→+∞

1

b→+∞

1

b→+∞

∞

то ∫ e−x2 dx теж збіжний.

1

+∫∞

Теорема 3. Якщо

збігається

невласний інтеграл

f (x)

dx ,

то

a

збігається інтеграл +∫∞f (x)dx .

a

Це є ознака абсолютної збіжності невласного інтеграла.

2.8.3 Невласні інтеграли необмежених функцій

Нехай функція f (x) на деякому скінченому проміжку в одній його

точці має безмежний розрив. Можливі такі випадки: функція має безмежний розрив на правому кінці, на лівому кінці, всередині проміжку.

1. Припустимо, що функція f (x) задана на проміжку [a,b] і точка

x = b є її точкою розриву другого роду, тобто lim f (x) = ∞ . Відпустимо

x→b

від точки x = b всередину проміжку на деяку величину ε > 0 . Оскільки на відрізку [a,b − ε ] функція f (x) неперервна, то існує визначений інтеграл

b−∫εf (x)dx . Якщо ε → 0, то відрізок [a,b − ε ] розтягується у відрізок [a,b],

a	b−∫εf (x)dx
при цьому інтеграл		буде функцією своєї верхньої межі I (ε ).
	a
Може статися, що за умови ε → 0, ця функція має скінчену границю.
Означення. Якщо існує		скінченна границя інтеграла	b−∫εf (x)dx за
			a

умови, що ε → 0, то цю границю називають невласним інтегралом функції

f (x) на проміжку

[a,b).

Позначають його символом

b∫ f (x)dx ,

в цьому

випадку невласний інтеграл називається збіжним.

a

Отже,

b∫ f (x)dx = lim b−∫εf (x)dx .

(2.19)

a

ε →0 a

Якщо ж lim I (ε ) не існує, то невласний інтеграл b∫ f (x)dx називається

ε →0

a

розбіжним.

Приклад

1.

Обчислити або

встановити

розбіжність невласного

1

dx

інтеграла ∫

.

1 − x 2

0

1

Розв’язування. Це є невласний інтеграл, бо функція f (x) =

в

1 − x 2

1

точці x =1 має безмежний розрив, оскільки

lim

= ∞. За означенням

1 − x2

1

1−ε

x→1

dx

dx

= lim arcsin x 10−ε

= lim (arcsin(1 − ε ) − arcsin 0)=

∫

= lim

∫

0

1 − x 2

ε →0

0

1 − x 2

ε →0

ε →0

= arcsin1 − 0 = π − 0 = π			. Отже, цей інтеграл збіжний.
	2	2	f (x) визначена і неперервна на проміжку (a,b] і в
2. Нехай функція
точці	x = a має	безмежний розрив, тобто lim f (x) = ∞ .			Відступивши
			x→a
вправо на деяку величину ε > 0 , розглянемо відрізок [a + ε ,b], на якому
функція неперервна, тому існуватиме визначений інтеграл				b∫ f (x)dx , який
при зміні ε стає функцією нижньої межі.				a+ε
					b∫ f (x)dx за
Означення.		Якщо при ε → 0 існує скінчена границя
					a+ε
умови,	що lim f (x) = ∞ , то її називають невласним інтегралом функції

x→a

f (x) на відрізку [a,b] і позначають символом b∫ f (x)dx .

	Отже,			b∫ f (x)dx =
				a
	Приклад			2. Обчислити або
	3	dx
	інтеграла ∫			.
		x − 1
	1

	a
lim	b∫ f (x)dx .	(2.20)
ε →0 a+ε
встановити розбіжність		невласного

Розв’язування. Оскільки функція

f (x) =

1

має безмежний розрив

x − 1

1

в точці x = 1, бо lim

= ∞ , то це є невласний інтеграл. За означенням

x

− 1

2 dx

2

x → 1

dx

2

(ln1 − ln ε ) = +∞

∫

= lim

∫

= lim ln

x −1

= lim

. Отже,

x −

1

ε →0

x −1

1+ε

ε →0

1

1+ε

ε →0

цей невласний інтеграл розбіжний.

3.Якщо функція має безмежний розрив в деякій внутрішній точці x = c проміжку [a,b], то за означенням

b∫ f (x )dx

a

де a < c < b і lim f (x)= ∞ .

x→c

= c∫	f (x )dx + b∫ f (x )dx ,	(2.21)
a	c

Якщо хоч би один із невласних інтегралів правої частини цієї рівності розбіжний, то невласний інтеграл лівої частини вважається

розбіжним.

Приклад		3. Обчислити або встановити розбіжність невласного
3	dx
інтеграла ∫		.
1 x ln x

2

Розв’язування. Підінтегральна функція має безмежний розрив в точці

3			dx	1			dx	3	dx
x = 1, тому ∫				= ∫				+ ∫		. Розглянемо перший із цих невласних
	1 x ln x				1 x ln x			1 x ln x
	2				2

1

dx

1−ε

dx

1−ε

d (ln x )

1−ε

інтегралів ∫

∫

∫

= lim

= lim

=

lim

ln

ln x

1

x ln x

x ln x

ln x

1

ε → 0

1

ε → 0

1

ε → 0

2

2

2

2

=

ln (1

− ε )

1

= lim

ln

− ln

ln

= −∞ . Отже, даний інтеграл розбіжний.

2

ε → 0

b

dx

Зауваження. Неважко переконати, що ∫

збіжний при p < 1 і

− x)p

розбіжний при p ≥ 1.

a (b

Нехай функція

f (x) має безмежний розрив в точці b , тобто

lim

f (x)= ∞.

Тоді справедлива така теорема

x→b−0

Теорема.

Якщо lim

f (x)

dx = K

≠ 0 ,

то при p < 1

невласний

1

x→b−0

(b − x)p

інтеграл b∫ f (x)dx збіжний, а при p ≥ 1

b∫ f (x)dx розбіжний.

a

a

Цю теорему використовують як ознаку при оцінці збіжності

невласних інтегралів від необмежених функцій.

1

dx

Приклад 4. Дослідити на збіжність невласний інтеграл ∫

.

1

0 3 1 − x 4

x = 1,

Розв’язування. Функція

f (x)= 3 1 − x4

має безмежний розрив в точці

тому

це невласний

інтеграл від

необмеженої

функції. При

	дослідженні на збіжність застосуємо приведену ознаку, взявши для
	порівняння функцію g(x) =	1	. Знайдемо границю відношення	f (x)
		1 − x		g(x)