
shpory_po_matem1
.docx![]()
21.Метод
трапеций. Приложение определённого
интеграла.Пусть
задана функция f(x)-непрепывная
на отрезке [a,b]
необходимо вычислить
 Разлбъём
отрезок [a,b]
на n-
равных частичных отрезков точками
A=x0<x1<…<xn=b,∆Xk
=Xk
-Xk-1=(b-a)/n,
k=1;n
Проведя прямые x=
Xk
, k=[0;n]
всю криволинейную трапецию разобьём
на n-частичных
криволинейных трапеций соединим 2-е
соседние точки( x(k-1);
f(
x
k-1)),
(x(k);
f(
x
k))Хордой
и рассмотрим n
прямоугольных трапеций Исходя из геом.
Смысла опр. Интеграла
Разлбъём
отрезок [a,b]
на n-
равных частичных отрезков точками
A=x0<x1<…<xn=b,∆Xk
=Xk
-Xk-1=(b-a)/n,
k=1;n
Проведя прямые x=
Xk
, k=[0;n]
всю криволинейную трапецию разобьём
на n-частичных
криволинейных трапеций соединим 2-е
соседние точки( x(k-1);
f(
x
k-1)),
(x(k);
f(
x
k))Хордой
и рассмотрим n
прямоугольных трапеций Исходя из геом.
Смысла опр. Интеграла![]()
 Пусть
y=f(xk),
тогда y=f(xk)
Пусть
y=f(xk),
тогда y=f(xk)![]() Для
наглядности на рисунке рассмотрена
неотрицательная ф-ция, однако по формуле
что выше имеет место для любой
интегрируемой на отрезке [a,b]
функции
f(x)
эта формула наз формулой
трапеций она
тем точнее чем больше число n,
в частности если функция f(x)
имеет 2-ую непрерывную производную то
абсолютная погрешность не
превосходит
Для
наглядности на рисунке рассмотрена
неотрицательная ф-ция, однако по формуле
что выше имеет место для любой
интегрируемой на отрезке [a,b]
функции
f(x)
эта формула наз формулой
трапеций она
тем точнее чем больше число n,
в частности если функция f(x)
имеет 2-ую непрерывную производную то
абсолютная погрешность не
превосходит![]() Приложение
опр. ИнтегралаИз
геом смысла опр интеграла следует, что
интервал от a,b
Приложение
опр. ИнтегралаИз
геом смысла опр интеграла следует, что
интервал от a,b
 ,численно равен S
криволин. трапеции ограниченной графиком
y=f(x),
прямыми x=a,
x=b,
и осью абсцисс (в случае если ф-ция f(x)
неотрицательная)
,численно равен S
криволин. трапеции ограниченной графиком
y=f(x),
прямыми x=a,
x=b,
и осью абсцисс (в случае если ф-ция f(x)
неотрицательная)
22.
Несобственные интегралыОпределённый
интеграл называется несобственным,
если выполняется, по крайней мере, одно
из следующих условий:1.Предел a или b
(или оба предела) являются бесконечными;
2.Функция f(x) имеет одну или несколько
точек разрыва внутри отрезка [a,
b].Интеграл
![]() называется абсолютно сходящимся, если
называется абсолютно сходящимся, если![]() сходится. Если интеграл сходится
абсолютно, то он сходится.
Интеграл
сходится. Если интеграл сходится
абсолютно, то он сходится.
Интеграл
![]() называется условно сходящимся, если
называется условно сходящимся, если
![]() сходится, а
сходится, а![]() расходится. Признак
Дирихле. Интеграл
расходится. Признак
Дирихле. Интеграл
![]() сходится, если: 1).функция
f(x) непрерывна и имеет ограниченную
первообразную на (a, b]; 2).функция g(x)
непрерывно дифференцируема и монотонна
на (a, b], причём.
сходится, если: 1).функция
f(x) непрерывна и имеет ограниченную
первообразную на (a, b]; 2).функция g(x)
непрерывно дифференцируема и монотонна
на (a, b], причём.
![]() Признак
Абеля. Интеграл сходится, если:
1).функция
f(x) непрерывна на (a, b] и интеграл сходится;
2).функция g(x) ограничена, непрерывно
дифференцируема и монотонна на (a, b], то
есть имеет конечный предел:.
Признак
Абеля. Интеграл сходится, если:
1).функция
f(x) непрерывна на (a, b] и интеграл сходится;
2).функция g(x) ограничена, непрерывно
дифференцируема и монотонна на (a, b], то
есть имеет конечный предел:.
№23.Понятие
числового ряда.Необход.условие
сходимости.
Пусть {аn}-числовая
послед-ть, где аn R,
n
R,
n N.
Выражение вида а1+а2+а3+…+аn+…=
N.
Выражение вида а1+а2+а3+…+аn+…= n
(1) наз.числовым рядом.Числа а1,а2,…аn
наз.членами
ряда,а аn-n-м
или общим членом ряда (1). Сумма первых
n-членов
ряда (1) наз. n-ой
частичной суммой данного ряда и обознач.
Sn:
Sn=
а1+а2+а3+…+аn=
n
(1) наз.числовым рядом.Числа а1,а2,…аn
наз.членами
ряда,а аn-n-м
или общим членом ряда (1). Сумма первых
n-членов
ряда (1) наз. n-ой
частичной суммой данного ряда и обознач.
Sn:
Sn=
а1+а2+а3+…+аn= к.
Имеем S1=a1,
S2=a1+a2,
S3=a1
+a2+a3,
Sn=
а1+а2+а3+…+аn.
Рассм.послед-ть частичных сумм ряда
(1) S1
,S2
...,Sn.
Если послед-ть частичных сумм { Sn
} имеет конечный предел S,то
числовой ряд (1) наз.сходящимся,а число
S
наз. Суммой ряда (1): S=
к.
Имеем S1=a1,
S2=a1+a2,
S3=a1
+a2+a3,
Sn=
а1+а2+а3+…+аn.
Рассм.послед-ть частичных сумм ряда
(1) S1
,S2
...,Sn.
Если послед-ть частичных сумм { Sn
} имеет конечный предел S,то
числовой ряд (1) наз.сходящимся,а число
S
наз. Суммой ряда (1): S= n
или
n
или
 n.
Если же предел послед-ти { Sn
} не существует или бесконечен,то ряд
(1) наз.расходящимся.
n.
Если же предел послед-ти { Sn
} не существует или бесконечен,то ряд
(1) наз.расходящимся.
24.Критерии
сходимости числового ряда.Основные
методы исчисления знакоположительного
ряда. Теорема
4:
для того что бы ряд сходился,необходимо
и достаточно что бы последовательность
его частичных сумм была ограниченной.
Теорема
5:
для сходимости ряда необходимо и
достаточно, что бы для любого
ε>0существовалл N(ε)
такой что при всяком натуральном р и
всех n>
N(ε)
имело место неравенство
│Sn+p-Sn│=│ │<εСходимость
или расходимость знакоположительного
ряда часто можно установить путём
сравнения его с другими рядами, о которых
известно сходятся они или нет. Теорема
6:пусть
даны два ряда с неотриц. членами
│<εСходимость
или расходимость знакоположительного
ряда часто можно установить путём
сравнения его с другими рядами, о которых
известно сходятся они или нет. Теорема
6:пусть
даны два ряда с неотриц. членами (обозначимА)и
(обозначимА)и
 ( обозначим В) и пусть an≤bn
тогда
из сходимости ряда В следует сходимость
ряда А, а из расходимости ряда А
расходимость ряда В. Теорема
7:
пусть даны два знакоположительных ряда
А и В если сущ. Конечный отличный от
нуля предел
( обозначим В) и пусть an≤bn
тогда
из сходимости ряда В следует сходимость
ряда А, а из расходимости ряда А
расходимость ряда В. Теорема
7:
пусть даны два знакоположительных ряда
А и В если сущ. Конечный отличный от
нуля предел
 =A
(0<А<∞), то ряды А и В одновременно
сходятся или расходятся. Теорема
8: пусть
дан ряд
=A
(0<А<∞), то ряды А и В одновременно
сходятся или расходятся. Теорема
8: пусть
дан ряд с положительными членами и сущ предел
с положительными членами и сущ предел =q
тогда при q<1
ряд сходится а при q>1
расходится. Теорема
9:если
для ряда
=q
тогда при q<1
ряд сходится а при q>1
расходится. Теорема
9:если
для ряда
 с
неотриц членами сущ предел
с
неотриц членами сущ предел
 =q
то при q<1
ряд сходится ,а при q>1
расходится. Теорема
10:
если члены знакоположительного ряда
=q
то при q<1
ряд сходится ,а при q>1
расходится. Теорема
10:
если члены знакоположительного ряда
 монотонно
убывают и сущ положительная невозрастающая
функция f(x)
такая что f(n)=an
при n≥1.
То ряд и несобственный интеграл
монотонно
убывают и сущ положительная невозрастающая
функция f(x)
такая что f(n)=an
при n≥1.
То ряд и несобственный интеграл сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
25.Знакочередющиеся
ряды.Абсолютная и условная сходимость.Ряд
называется знакочередующимся, если
его члены попеременно принимают значения
противоположных знаков, т. е.:![]() Теорема Лейбница о сходимости
знакочередующихся рядов.Признак
Лейбница — признак сходимости
знакочередующегося ряда, установлен
Готфридом Лейбницем. Формулировка
теоремы:
Пусть
для знакочередующегося ряда
Теорема Лейбница о сходимости
знакочередующихся рядов.Признак
Лейбница — признак сходимости
знакочередующегося ряда, установлен
Готфридом Лейбницем. Формулировка
теоремы:
Пусть
для знакочередующегося ряда![]() выполняются
следующие условия:
выполняются
следующие условия:![]()
![]() тогда ряд сходится. Если, выполнены
все условия, и ряд из модулей сходится,
то исходный ряд сходится абсолютно.
Если выполнены все условия, но ряд из
модулей расходится, то исходный ряд
сходится условно. Строгая положительность
а-n
существенна. Ряды, удовлетворяющие
признаку Лейбница, называются рядами
Лейбница. Следует отметить, что этот
признак является достаточным, но не
необходимым
тогда ряд сходится. Если, выполнены
все условия, и ряд из модулей сходится,
то исходный ряд сходится абсолютно.
Если выполнены все условия, но ряд из
модулей расходится, то исходный ряд
сходится условно. Строгая положительность
а-n
существенна. Ряды, удовлетворяющие
признаку Лейбница, называются рядами
Лейбница. Следует отметить, что этот
признак является достаточным, но не
необходимым
26.Знакопеременные
ряды. Сходимость.Числовой
ряд
 п,содер
бесконеч множество положит и бесконеч
множество отриц членов наз знакопеременным.
Теорема 1Пусть дан знакопеременный ряд
∑ап(1).Если
сходится ряд ∑│ап│(2)
составленный из модулей членов данного
ряда (1)сходится и знакопеременный
ряд(1).Ряд (1)наз абсолютно сходящимся,если
ряд (2)сходится.Если же ряд(1)сходится,а
ряд(2)расходится,то ряд(1)наз условно
сходящимся.Св-ва обсолютно сходящихся
рядов:1).Если ряд(1)абсолютно сходится
и имеет сумму S,то ряд,полученный из
него перестановкой членов также сходится
и имеет ту же сумму S,что и исходный
ряд(1).2)Абсолютно сходящиесь ряды
п,содер
бесконеч множество положит и бесконеч
множество отриц членов наз знакопеременным.
Теорема 1Пусть дан знакопеременный ряд
∑ап(1).Если
сходится ряд ∑│ап│(2)
составленный из модулей членов данного
ряда (1)сходится и знакопеременный
ряд(1).Ряд (1)наз абсолютно сходящимся,если
ряд (2)сходится.Если же ряд(1)сходится,а
ряд(2)расходится,то ряд(1)наз условно
сходящимся.Св-ва обсолютно сходящихся
рядов:1).Если ряд(1)абсолютно сходится
и имеет сумму S,то ряд,полученный из
него перестановкой членов также сходится
и имеет ту же сумму S,что и исходный
ряд(1).2)Абсолютно сходящиесь ряды
 п
и
п
и
 п
с суммами S1 и S2 можно почленно
складывать(вычислять).В итоге получится
абсолютно сход ряд,сумма которого равна
S1+S2
(S1-S2).Произведение
2 рядов
п
с суммами S1 и S2 можно почленно
складывать(вычислять).В итоге получится
абсолютно сход ряд,сумма которого равна
S1+S2
(S1-S2).Произведение
2 рядов
 п
и
п
и
 п
наз ряд вида(а1б1)+(а1б2+а2б1)+(а1б3+а2б2+а3б1)+…+(
а1бп+а2бп-1+…+апб1)+…Произведение 2
абсолютно сходящихся рядов с суммами
S1 и S2 есть бесконечно сход ряд,сумма
которого= S1*S2.Теорема
Римоно:Если ряд(1)сходится неабсолютна
,то какое бы ни взять число S,можно
так переставить члены в этом ряду,чтобы
преобразованный ряд имел своей суммой
именно S.
п
наз ряд вида(а1б1)+(а1б2+а2б1)+(а1б3+а2б2+а3б1)+…+(
а1бп+а2бп-1+…+апб1)+…Произведение 2
абсолютно сходящихся рядов с суммами
S1 и S2 есть бесконечно сход ряд,сумма
которого= S1*S2.Теорема
Римоно:Если ряд(1)сходится неабсолютна
,то какое бы ни взять число S,можно
так переставить члены в этом ряду,чтобы
преобразованный ряд имел своей суммой
именно S.
27.
Степенные ряды. Сходимость степенного
ряда. Опр.
Функциональный
ряд вида
 ,(1), где
,(1), где
 ,
,
 ,
наз-ся степенным рядом. Числа
,
наз-ся степенным рядом. Числа
 ,
,
 ,
…,
,
…,
 ,
… наз-ся коэффициентами степенного
ряда (1). Если
,
… наз-ся коэффициентами степенного
ряда (1). Если
 ,
то ряд (1) имеет вид
,
то ряд (1) имеет вид
 ,
(2). Будем рассматривать только такие
степенные ряды, т.к. полагая в (1)
,
(2). Будем рассматривать только такие
степенные ряды, т.к. полагая в (1)
 ,
получаем ряд вида (2).Степенной ряд (2)
всегда сходится в точке х=0. Если х≠0,
то ряд (2) может сх-ся или расх-ся.Т1
(Абеля). Если степенной ряд (2) сх-ся в т.
х0≠0,
то во всех точках х, |х|<|х0|,
он схся абсолютно. Если в т. х1≠0
степ. ряд (2) расх-ся, то он расходится
во всех точках х, |х|>|х1|.
Теор. Абеля дает ясное
представление об области сходимости
степенного ряда. Для наглядности
воспользуемся следующим приемом:
окрасим мысленно в зеленый цвет каждую
точку сходимости ряда (2), а в красный
цвет – каждую точку расходимости ряда
(2). Очевидно, что т. х=0 будет всегда
окрашена в зеленый цвет. Если степенной
ряд сходится всюду на R,
то вся числовая ось будет зеленой. Если
степ. ряд везде расходится, то вся
числовая ось, кроме т. х=0, будет красной.
Если какая-нибудь точка х0≠0
будет окрашена в зеленый, то зелеными
будут все точки лежащие между х0
и
х=0,
а также между -х0
и
х=0.
Если какая либо точка х1>0
будет красной, то будут красными все
точки лежащие правее х1.
Если х1<0
будет красной, то будут красными все
точки лежащие левее х1.
Т.к. каждая точка числовой оси будет
либо зел. либо красн., то идя от т. х=0
вправо по числовой оси сначала будем
встречать только зел. точки, а затем –
только красные, причем граничная или
разделяющая эти разноцветные участки
точка R
может быть как красн., так и зел. цвета
(в зависимости от того сходится ряд на
границе или расх.) То же самое можно
сказать, если идти налево от точки х=0
в частности в т. х=-R
ряд может сходиться или расх-ся.
,
получаем ряд вида (2).Степенной ряд (2)
всегда сходится в точке х=0. Если х≠0,
то ряд (2) может сх-ся или расх-ся.Т1
(Абеля). Если степенной ряд (2) сх-ся в т.
х0≠0,
то во всех точках х, |х|<|х0|,
он схся абсолютно. Если в т. х1≠0
степ. ряд (2) расх-ся, то он расходится
во всех точках х, |х|>|х1|.
Теор. Абеля дает ясное
представление об области сходимости
степенного ряда. Для наглядности
воспользуемся следующим приемом:
окрасим мысленно в зеленый цвет каждую
точку сходимости ряда (2), а в красный
цвет – каждую точку расходимости ряда
(2). Очевидно, что т. х=0 будет всегда
окрашена в зеленый цвет. Если степенной
ряд сходится всюду на R,
то вся числовая ось будет зеленой. Если
степ. ряд везде расходится, то вся
числовая ось, кроме т. х=0, будет красной.
Если какая-нибудь точка х0≠0
будет окрашена в зеленый, то зелеными
будут все точки лежащие между х0
и
х=0,
а также между -х0
и
х=0.
Если какая либо точка х1>0
будет красной, то будут красными все
точки лежащие правее х1.
Если х1<0
будет красной, то будут красными все
точки лежащие левее х1.
Т.к. каждая точка числовой оси будет
либо зел. либо красн., то идя от т. х=0
вправо по числовой оси сначала будем
встречать только зел. точки, а затем –
только красные, причем граничная или
разделяющая эти разноцветные участки
точка R
может быть как красн., так и зел. цвета
(в зависимости от того сходится ряд на
границе или расх.) То же самое можно
сказать, если идти налево от точки х=0
в частности в т. х=-R
ряд может сходиться или расх-ся.
![]()
Опр.
Число
R
наз-ся радиусом сходимости ряда (2),
интервалом (-R,R)
– интервалом сходимости. Если ряд (2)
сх-ся только в т. х=0, то R=0;
если ряд сх-ся для всех х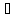 R,
то R=+∞.
Подчеркнем, что в кажд. т. х
R,
то R=+∞.
Подчеркнем, что в кажд. т. х (-R,R)
ряд (2) будет сх-ся абсолютно, в точках
х=±R
может сх-ся или расх-ся.
Т2
Если
сущ-ет предел
(-R,R)
ряд (2) будет сх-ся абсолютно, в точках
х=±R
может сх-ся или расх-ся.
Т2
Если
сущ-ет предел
 ,
то радиус сходимости R
ряда (2) равен
,
то радиус сходимости R
ряда (2) равен
 , т.е.
, т.е.
 .
Т3
Если
сущ-ет
.
Т3
Если
сущ-ет
 ,
то
,
то
 .
Сформулируем основные свойства степенных
рядов (2) с интервалом сходимости (-R;R):
1. Степенной ряд (2) сх-ся
равномерно на любом отрезке, содержащемся
в (-R;R).
2. Сумма S(x)
степенного ряда (2) явл-ся непрерывной
ф-цией в интервале сходимости (-R;R).
3. Ст. ряды
.
Сформулируем основные свойства степенных
рядов (2) с интервалом сходимости (-R;R):
1. Степенной ряд (2) сх-ся
равномерно на любом отрезке, содержащемся
в (-R;R).
2. Сумма S(x)
степенного ряда (2) явл-ся непрерывной
ф-цией в интервале сходимости (-R;R).
3. Ст. ряды
 и
и
 , имеющие радиусы сход-сти соотв-но R1
и R2,
можно почленно складывать, вычитать и
умножать, причем радиус сходится
полученных т.о. рядов равен меньшему
из чисел R1
и R2.
4.
Ст. ряд (2) внутри интервала сх-сти (-R;R)
можно почленно дифференцировать.
5. Ст. ряд (2) можно почленно
интегрировать на каждом отрезке,
расположенном внутри интервала сх-сти
(-R;R).Отметим,
что св-ва 1-5 справедливы и для ст. рядов
вида (1).
, имеющие радиусы сход-сти соотв-но R1
и R2,
можно почленно складывать, вычитать и
умножать, причем радиус сходится
полученных т.о. рядов равен меньшему
из чисел R1
и R2.
4.
Ст. ряд (2) внутри интервала сх-сти (-R;R)
можно почленно дифференцировать.
5. Ст. ряд (2) можно почленно
интегрировать на каждом отрезке,
расположенном внутри интервала сх-сти
(-R;R).Отметим,
что св-ва 1-5 справедливы и для ст. рядов
вида (1).
28.
Разложение функций в степенные ряды.
Ряд Тейлора. Для
любой функции f(х),
определённой в окрестности точки а и
имеющей в ней производные до (n+1)-ого
порядка включительно, справедлива
формула Тейлора: (1),
где Rn(x)
– остаточный член формулы Тейлора.
(1),
где Rn(x)
– остаточный член формулы Тейлора.
 ,
,
 ,
,
 .
Соотношение (1) запишем в виде
.
Соотношение (1) запишем в виде
 (2),
где Pn(x)
– многочлен Тейлора:
(2),
где Pn(x)
– многочлен Тейлора:
 (3).
Если функция
f(x)
бесконечно дифференцируема в окрестности
точки а и остаточный член Rn(x)
стремится к нулю при n→∞,
то из формулы Тейлора получим разложение
функции f(x)
по степеням (х-а), называемое рядом
Тейлора:
(3).
Если функция
f(x)
бесконечно дифференцируема в окрестности
точки а и остаточный член Rn(x)
стремится к нулю при n→∞,
то из формулы Тейлора получим разложение
функции f(x)
по степеням (х-а), называемое рядом
Тейлора:
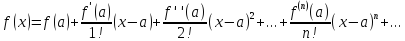 (4).
Ряд Тейлора (4) можно составить для любой
бесконечно дифференцируемой функции
в окрестности точки а. такой ряд может
оказаться расходящимся или сходящимся,
но не к функции f(x).теорема1
Ряд Тейлора (4) функции f(x) сходится к
f(x) в точке х из некоторой окрестности
точки а тогда и только тогда, когда в
этой точке х остаточный член формулы
Тейлора (1) сходится к 0 при х→∞. отметим,
что проверка условия теоремы 1 во многих
случаях вызывает трудности, поэтому
на практике часто используют достаточное
условие разложимости функции в ряд
Тейлора, которое выражается следующей
теоремой. Теорема2.
Если функция
f(x) имеет производные любого порядка
на интервале (а-δ;а+δ) и все её производные
ограничены одной и той же константой
М на (а-δ;а+δ), то ряд Тейлора (4) сходится
к функции f(x)
на (а-δ;а+δ).
(4).
Ряд Тейлора (4) можно составить для любой
бесконечно дифференцируемой функции
в окрестности точки а. такой ряд может
оказаться расходящимся или сходящимся,
но не к функции f(x).теорема1
Ряд Тейлора (4) функции f(x) сходится к
f(x) в точке х из некоторой окрестности
точки а тогда и только тогда, когда в
этой точке х остаточный член формулы
Тейлора (1) сходится к 0 при х→∞. отметим,
что проверка условия теоремы 1 во многих
случаях вызывает трудности, поэтому
на практике часто используют достаточное
условие разложимости функции в ряд
Тейлора, которое выражается следующей
теоремой. Теорема2.
Если функция
f(x) имеет производные любого порядка
на интервале (а-δ;а+δ) и все её производные
ограничены одной и той же константой
М на (а-δ;а+δ), то ряд Тейлора (4) сходится
к функции f(x)
на (а-δ;а+δ).
30.Понятие диф ур-нияю Решение диф ур-ний с разделяющимися переменными.Пусть x − независимая переменная, y= y(x) − искомая неизвестная функция. Дифференциальным уравнением называют уравнение, содержащие производную или производные неизвестной функции. Уравнения вида y' = f( x, y )называют дифференциальными уравнениями 1-го порядка, разрешенными относительно производной.Уравнения вида f(x,y,y’)=0 называют дифференциальными уравнениями 1-го порядка. Дифференциальные уравнения вида y ‘=g( y )*f (x) называют уравнениями с разделяющимися переменными. Решение уравнений с разделяющимися переменными осуществляется по следующей схеме: dy/dx=f (x)* g (y) ⇒dy/ g (y) =f(x)dx⇒ ∫dy /g(y)= ∫ f(x) dx .
34.Диф ур-ния высших порядков.Метод Эйлера.
Диф.урав
n-ого порядка
наз.урав.вида f(х, y, y…’, )=0.Решением
такого урав.служит всякая,
)=0.Решением
такого урав.служит всякая,
n
раз непрерывно диф.ф-ция y= (х),опред.на
некатором интервале(а,b) и обращ.данное
урав.втождество.Урав.Ф(х,y,С1,С2…С
(х),опред.на
некатором интервале(а,b) и обращ.данное
урав.втождество.Урав.Ф(х,y,С1,С2…С )=0
определяющ. Общее решение как неявную
ф-цию,наз.общим интегралом диф.урав.Линейным
однород.урав.n-ого порядка с постоян.коэфиц.
наз. урав
)=0
определяющ. Общее решение как неявную
ф-цию,наз.общим интегралом диф.урав.Линейным
однород.урав.n-ого порядка с постоян.коэфиц.
наз. урав +а1
+а1 +а2
+а2 +…+
+…+ y’+
y’+ y=0
y=0
y=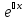 ,
, +а1
+а1 +…+
+…+ ԓ+
ԓ+ =0
это урав.наз. характеристическим .
Решен.однородного диф.урав.
=0
это урав.наз. характеристическим .
Решен.однородного диф.урав.
свелось к решен.алгебраич. урав.,этот м-д наз.м-дом Эйера.
31.Понятие диф ур-ния. Решение однородных диф ур-ний.При реш. различных задач матем., физ,. химии и др наук часто исп-ся ур-ния,связывающие независимую переменную,искомую ф-цию и не производные. Такие ур-ния наз-с дифференциальными. Если искомая ф-ла зависит от 1 переменной,то дифф.ур. наз.обыкновенным. если искомая ф-ция зависит от неск.переменных,то диф.ур. наз.ур-нием в частных производных. Наивысший порядок производной,входящий в диф.ур.,наз. порядком этого ур-ния.Диф.ур. P(x,y)dx+Q(x,y)dy=0 наз.однородным,если ф. P(x,y)и Q(x,y) (1)-однородные ф-ции одной степени. Разделив ур.(1) относит. произодн. dy\dx, запишем dy\dx=f(x,y) (2),где f(x,y)-однородная ф-ция нулевой степени. Покажем,что с пом.замены y=ux,где u=u(x),однор. ур-ние сводится к ур-нию с разделяющимися переменными. Пусть t=1\х. подст. t в 1,получ. (1\tm)P(1;y\x)dx+ (1\tm)Q(1;y\x)dx=0. Учит.,что dy\dx=u+x(dy\dx), имеем P(1;u)+Q(1,u)+xQ(1,u)(du\dx)=0. Получ. (Q(1,u)du)\(P(1,u)+uQ(1,u)=-dx\x –ур-ние с раздел.переменными. При делении перем. могли быть утеряны решения вида u=a, где а-корень ур-ния P(1;u)+uQ(1,u)=0.
33.
Уравнение Бернулли. Дифференциальные
уравнения в полных дифференциалах.Решением
линейное неоднородного уравнение
y`+p(х)у=q(x)
(7)
Решение будем искать в виде:
у=C(x) (8) Где C(x)-
неизвестная функция подставляя (8) и
(7), имеем: С
(8) Где C(x)-
неизвестная функция подставляя (8) и
(7), имеем: С (х)
(х) +С(х)
+С(х) +С(х)р(х)
+С(х)р(х) =
q(x)
С(х)
=
q(x)
С(х) =0
Значит, С
=0
Значит, С (х)
(х) =
q(x)
=
q(x) =
= C(x)=
C(x)= dx+C
Подставляя найденное С(х) в (8), получим
формулу Бернулли y=C
dx+C
Подставляя найденное С(х) в (8), получим
формулу Бернулли y=C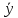 +
+ dx
Описанный метод решения уравнения
(7) наз. методом вариации произвольной
постоянной или методом методом Лагранжа.
Др. методом решения линейного уравнения
явл метод Бернулли , кот. заключается
в след.:Решение уравнения(7) ищем в виде
y=uv,
где u(x)
и v(x)-
непрерывно дифференцинцируемые на I
функции, причём u(x)
dx
Описанный метод решения уравнения
(7) наз. методом вариации произвольной
постоянной или методом методом Лагранжа.
Др. методом решения линейного уравнения
явл метод Бернулли , кот. заключается
в след.:Решение уравнения(7) ищем в виде
y=uv,
где u(x)
и v(x)-
непрерывно дифференцинцируемые на I
функции, причём u(x) 0,
v(x)
0,
v(x) 0.
После подстановки y
в (7) и учитывая, что
0.
После подстановки y
в (7) и учитывая, что
 =
u
=
u +v
+v Получим
u
Получим
u +v
+v +p(x)uv=q(x)(9)Потребуем,
чтобы v(
+p(x)uv=q(x)(9)Потребуем,
чтобы v( +p(x)u)=0
, будем иметь
+p(x)u)=0
, будем иметь +p(x)u=0
(10)Или
+p(x)u=0
(10)Или
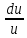 =
p(x)dx.
Подставляя частное решение этого
уравнения u=
=
p(x)dx.
Подставляя частное решение этого
уравнения u= в (9), с учётом (10) получим dv=
в (9), с учётом (10) получим dv=
 q(x)dx,
а v=
q(x)dx,
а v= +C.
Окончательно, y=
+C.
Окончательно, y=
 Уравнением
Бернулли наз. нелинейное диф. Уравнение
первого порядка вида: y`+p(x)y=q(x)
Уравнением
Бернулли наз. нелинейное диф. Уравнение
первого порядка вида: y`+p(x)y=q(x) (11)
Где α(α
(11)
Где α(α α
α 1)
– произвольное вещественное число
подстановка u=
1)
– произвольное вещественное число
подстановка u= приводит уравнение (11) к линейному
неоднородному уравнению. Уравнение(11)
можно решать также подстановкой
y(x)=u(x)v(x).
Тогда, записав уравнение(11) в виде
u`v+(v`+p(x)v)u=q(x)
приводит уравнение (11) к линейному
неоднородному уравнению. Уравнение(11)
можно решать также подстановкой
y(x)=u(x)v(x).
Тогда, записав уравнение(11) в виде
u`v+(v`+p(x)v)u=q(x) ,
решим два уравнения с разделяющимися
переменными: v`+p(x)v=0(берём
только 1 решение v
,
решим два уравнения с разделяющимися
переменными: v`+p(x)v=0(берём
только 1 решение v 0)
и u`=q(x)
0)
и u`=q(x) (берём
его общее решение) Подставляя найденные
u
и v
в соотношение y(x)=u(x)v(x),
получим общее решение уравнения
Бернулли. Уравнение
вида:P(x,y)dx+Q(x,y)dy=0(12)наз
уравнением в полных дивверенциалах,
если его левая часть явл полным
дифференциалом некоторой функции u
,т.е. P(x,y)dx+Q(x,y)dy=du(x,y)(13)
(берём
его общее решение) Подставляя найденные
u
и v
в соотношение y(x)=u(x)v(x),
получим общее решение уравнения
Бернулли. Уравнение
вида:P(x,y)dx+Q(x,y)dy=0(12)наз
уравнением в полных дивверенциалах,
если его левая часть явл полным
дифференциалом некоторой функции u
,т.е. P(x,y)dx+Q(x,y)dy=du(x,y)(13)
7.точка а – точка разрыва f(x) если f(x) не является непрерывной в этой точке.если x=a – точка разрыва y=f(x) то в ней не выполняется по крайней мере одно из условий 1-ого определения непрерывности функции а именно:1. Функция определена в некоторой окрестности точки а, но не определена в самой точке а. 2. Функция определена в точке а и её окрестности но не существует limx→a f(x). 3. Функция определена в точке а и её окрестности и существует limx→a f(x) но он ≠f(a). Точка а – точка разрыва 1-ого рода функции y=f(x) если в этой точке существуют конечные односторонние пределы функции т.е. limx→a-0 f(x)=А1, limx→a+0 f(x)=А2 при этом:а) если А1=А2 то точка а – точка устранимого разрыва. б)если А1≠А2 то точка а – точка конечного разрыва значения (А1-А2)- скачок функции в точке разрыва x=a. Точка а – точка разрыва 2-ого рода y=f(x) если по крайней мере 1 из односторонних пределов не существует.
29.
Представление элементарных ф-ций рядом
Маклорена.
Ряд
Тейлора
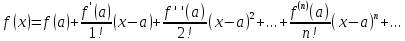 Если а=0, то он наз-ся рядом Маклорена.
При разложении ф. f(x)
в ряд Макл.
Если а=0, то он наз-ся рядом Маклорена.
При разложении ф. f(x)
в ряд Макл.
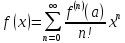 (1)
поступаем так: вычисляем значения ф.
f(x)
и ее производных f’(x),
f”(x),…,
f(n)(x),…
. В точке х=0: записываем ряд (1) и находим
его интервалом сходимости, определяем
интервалом (-R;R),
в кот. остаточный член
(1)
поступаем так: вычисляем значения ф.
f(x)
и ее производных f’(x),
f”(x),…,
f(n)(x),…
. В точке х=0: записываем ряд (1) и находим
его интервалом сходимости, определяем
интервалом (-R;R),
в кот. остаточный член
 при
при
 (если такой интервал сущ-ет, то на нем
справедливо разложение (1)). а) пусть
f(x)=ех,
f(n)(x)=
ех,
при х=0 f(n)(0)=1.
Ряд Маклорена будет иметь вид
(если такой интервал сущ-ет, то на нем
справедливо разложение (1)). а) пусть
f(x)=ех,
f(n)(x)=
ех,
при х=0 f(n)(0)=1.
Ряд Маклорена будет иметь вид
 .
б) пусть f(x)=sin
x,
f(n)(x)=sin(x
+
.
б) пусть f(x)=sin
x,
f(n)(x)=sin(x
+
 ),
, при х=0 f(0)=0,
f’(0)=1,
f”(0)=0,
f’’’(0)=-1,
f(4)(0)=0,
… Ряд Маклорена будет иметь вид
),
, при х=0 f(0)=0,
f’(0)=1,
f”(0)=0,
f’’’(0)=-1,
f(4)(0)=0,
… Ряд Маклорена будет иметь вид
 .
Тогда имеем
.
Тогда имеем
 .в) аналогично
.в) аналогично
 .г) разложим ф. f(x)=ln(1+x)
в ряд Макл.
.г) разложим ф. f(x)=ln(1+x)
в ряд Макл.
 ,
,
 .д)
.д)
 ,
,
 .
При х=1 имеем
.
При х=1 имеем
 ;при х=-1
;при х=-1
 .
Эти ряды сходятся условно.е) разложение
в ряд степенной ф. (1+х)α,(α≠0).
.
Эти ряды сходятся условно.е) разложение
в ряд степенной ф. (1+х)α,(α≠0).
 .
.
35. Метод Эйлера решения диф.ур.Пусть λ1, λ2, λ3,…, λn –корни ур-ния λn+a1 λn-1+…+an-1 λ+an=0 (3),причем среди них могут быть и кратные(повторяющиеся).Возм.след.случаи:1) λ1, λ2, λ3,…, λn-вещественные и различные.Тогда фундаментальная система реш. ур-ния y(n)+a1y(n-1)+a2y(n-2)+…+an-1y`+any=0 (1) имеет вид: еλ1х, еλ2х, …, еλnх (4),а общ.решением эт.ур-ния будет: Ў=С1еλ1х+С2 еλ2х+…+Сn еλnх. где С1,С2,…,Сn-произвольные постоянные. 2) Корни характеристического ур-ния вещественные, но среди них есть кратные.Пусть,например, λ1=λ2=…= λк, т.е. λ1 явл. к-кратным корнем ур-ния (3),а все ост. (n-k) корней различные.Фундаментальная сист. решений ур-ния (1)в эт.случ.: еλ1х, хеλ1х, …,хк-1 еλ1х, еλк+1х, еλnх, (5),а общ.реш. Ў=С1еλ1х+С2х еλ1х+…+ Скхк-1еλ1х + Ск+1 еλл+1х +Сn еλnх .3) Среди хар-ого ур. (3)есть комплексные. Пусть для определенности λ1=α+iβ, λ2=α-iβ, λ3=υ+iδ,λ4=υ-iδ,а ост.корни вещественные и различные.Поскольку коэффициенты ai, i=от 1до n, ур-ния (3)вещественные,то комплексные корни этого ур-ния попарно сопряженные.Согласно у=еλх (2) будем иметь: у1= еλ1х=е(α+iβ)х=eαx(cosβx+isinβx), у2=eαx(cosβx-isinβx), у3=eυx(cosδx+isinδx), у4=eυx(cosδx-isinδx), у5=eλ5x,…, уn=eλnx.Фунд.сист.реш.:еαхcosβx,еαхsinβx,еυхcosδx,еυхsinδx,eλ5x,…,eλnx, (6). Ў=С1еλхcosβ+С2 еλхsinβ+C3еυхcosδx+C4 еυхsinδx +C5 eλ5x +Cn еλnх .Общ.реш.4) Пусть λ1=α+iβ явл. к-кратнымкорнем ур.(3 ) (к<=n\2), λ2=α-iβ также будет к-кратн.корнем и пусть ост.корни веществ.и различны. фунд.сист.реш.ур.(1): еαхcosβx,еαхsinβx,хеλхcosβx,хеλхsinβx,…,хк-1еλхcosβx, хк-1еλхsinβx, еλ2к+1х,…,eλnx (7). Общ.реш.диф.ур.1 запишется: Ў=С1еαхcosβx+С2еαхsinβx+С3хеλхcosβx+С4хеλхsinβx,…,С2к-1хк-1еλхcosβx+C2k хк-1еλхsinβx+С2к+1еλ2k+1х+…+Cneλnx
13.
Основные
теоремы дифференциального исчисления.
Теорема Ферма. Пусть функция f
определена на интервале (а;b)
и в некоторой точке х0ϵ(а;b)
имеет локальный экстремум. Тогда если
в точке х0
существует производная то она равна
0, т.е. f'(x0)=0.
Теорема Ролля. Пусть функция f непрерывна
на отрезке [a;b]
, дифференцируема на интервале (а;b),
и на концах отрезка [a;b] принимает равные
значения, то есть f(a)=f(b).
Тогда существует точка cϵ
(а;b), в которой f'(c)=0.
Теорема Лагранжа. Если функция f
непрерывна на отрезке [a;b], дифференцируема
на интервале (а;b), то существует точка
cϵ(а;b),такая, что справедлива формула: .
Теорема Коши. Если функция f
и g
непрерывны на отрезке [a;b],
дифференцируема
на интервале (а;b), причём g'(x)≠0,
то существует точка cϵ(а;b),такая, что
справедливо равенств
.
Теорема Коши. Если функция f
и g
непрерывны на отрезке [a;b],
дифференцируема
на интервале (а;b), причём g'(x)≠0,
то существует точка cϵ(а;b),такая, что
справедливо равенств о:.
о:.
-
Пусть N – множество натур чисел. Если каждому натур числу n поставлено в соответствие некоторое число xn, то говорят, что определена числовая последовательность х1, х2,…, хn. Числа хn назыв элементарными или членами последовательности. Числовую последовательность будем записывать в виде {xn}. Последовательности {xn+yn}, {xn-yn}, {xnyn},
 назыв соответственно суммой, разностью,
произведением и частным двух
последовательностей {xn}
и {yn}.
Последовательность {xn}
назыв ограниченной, если существуем
М>0
такое, что для любого nϵN:
назыв соответственно суммой, разностью,
произведением и частным двух
последовательностей {xn}
и {yn}.
Последовательность {xn}
назыв ограниченной, если существуем
М>0
такое, что для любого nϵN:
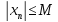 .
Последовательность {xn}
назыв неограниченной, если для любого
М>0
существует nϵN:
.
Последовательность {xn}
назыв неограниченной, если для любого
М>0
существует nϵN:
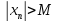 .
.
