otd

В случае пересечения областей диагнозов статистические распределения плотности вероятности диагностического параметра x для дефектных D2 и исправных D1 подшипников имеют вид, показанный на рис. 3.1.

f x / Di

D1

f x / D
1

D2

f x / D
2

х1

х0

х2

х

Рис. 3.1. Статистические распределения плотности вероятности диагностического параметра x для исправного D1 и дефектного D2 состояний объекта.

Так как области D1 и D2 пересекаются, то, в принципе, невозможно выбрать значение xо, при котором всегда соблюдалось бы правило (3.1) и не было ошибочных

решений. Поэтому практическая задача состоит в выборе оптимального xо по каким либо критериям. Рассмотрим сначала возможные ошибки при принятии решения.

Ложная тревога – случай, когда принимается решение о наличии дефекта, а в действительности объект находится в исправном состоянии.

Пропуск дефекта – случай принятия решения об исправном состоянии, в то время когда объект содержит дефект.

Обозначим Hij возможные решения по правилу (3.1) (первый индекс соответствует принятому решению, второй – действительному состоянию, 1 – соответствует исправному состоянию, 2 – дефекту), тогда:

Н11 - правильное решение об исправном состоянии; Н22 – правильное решение о дефектном состоянии; Н12 – пропуск дефекта; Н21 – ложная тревога.

Вероятность ложной тревоги Р(Н21), случай, когда при x xо объект является исправным, но по правилу (3.1) оценивается как дефектный, равна вероятности

произведения двух событий: диагноз D1 и значение x xо при исправном состоянии.

. Вероятность x xо при исправном состоянии (условная вероятность ложной тревоги) определяется площадью, ограниченной кривой плотности вероятности исправного состояния при x xо

P x x

/ D

f x / D .dx

o

,

(3.2)

1

1

x

o

тогда вероятность ложной тревоги будет равна произведению

вероятностей диагноза D1

и значения x xо

P H

P D .P x x

P

f x / D .dx ,

21

o

/ D

(3.3)

1

1

1

1

x

o

где Р1=P(D1) – априорная вероятность диагноза D1, принимается на базе

статистических данных.

Аналогично находится вероятность пропуска дефекта:

х

P H12 P D2 P x xo / D2 P2

о

f x / D2 .dx .

(3.4)

Для выбора оптимального xо необходимо дать оценку той и другой ошибке. После этого можно использовать различные методы выбора, то есть принятия решения на основе оценки возможного риска.

Для определения среднего риска принимаем цену ложной тревоги С21 и цену пропуска дефекта С12, тогда средний риск определится выражением

							0
				f x / D	dx C		x	f x / D	dx ,
R C	21	P				P				(3.5)
		1		1	12	2		2
			x
			0

С21 и С12 – условные значения, оценивающие последствия пропуска дефекта

и ложной тревоги, как правило, принимается С12 С21. В общем случае вводят цену правильных решений, умножая ее, соответственно, на вероятности соответствующих правильных решений, при этом цена правильного решения принимается отрицательной. Выражение (3.5) представляет собой среднее значение (математическое ожидание) риска при

заданном значении х0. Но для оптимизации решения необходимо задаться каким-то критерием, и в этом случае наиболее оправдан критерий

минимального риска.

Метод минимального риска: находят условие минимума среднего риска. Дифференцируя (3.5) по xо и приравнивая производную нулю получают условие экстремума

dR	C	P f x			/ D	C	P f x		/ D 0 ,	(3.6)
dx0		21	1	0	1	12	2	0	2

в практических задачах сложно дать численную оценку стоимости ошибок, но проще задаться их соотношением, тогда из формулы (3.6) имеем

f x		0	/ D
f x			1
	0		/ D
			2



	C		P
	12			2
	C	21		P
				1

.

(3.7)

Это условие может определять два значения xо – по минимуму и по максимуму. Для того, чтобы получить не только необходимое, но и достаточное условие

	минимума, вторая производная должна быть больше нуля ,	d 2 R		0
		dx	2 0

для одномодальных распределений можно ограничиться выбором х0 в пределах

x1 x0	x2	(3.8)

В соответствии с правилом (3.1) по методу наименьшего риска принимается следующее решение о состоянии объекта, имеющего данное значение параметра x

			x D , если	f x / D
				1					;	(3.9)
				f x / D
			1
				2
			x D , если	f x / D1		,				(3.10)
			2	f x / D2
	C12P2		представляет собой пороговое значение для
	C P
	21	1

отношения правдоподобия – отношение плотностей вероятностей распределения x при двух состояниях.

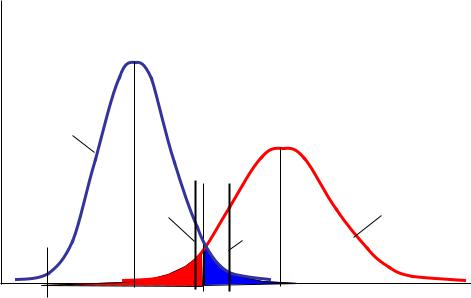
В нашем примере: Р2=0,002; Р1=0,998, примем отношение С12/С21 = 1000, получим = 2,004.

Соответственно при С12/С21 = 100 получим = 0,2004.

f x / Di

D1

f x / D	D2
1

=2

=0,2

f x / D
2

х1

х0

х2

х

Метод минимального риска является наиболее оптимальным и общим. Когда сложно, либо невозможно, дать оценку соотношения цены ложной тревоги и пропуска дефекта, либо нет априорных данных для определения вероятности того или иного состояния объекта, используют другие методы.

Метод минимального числа ошибочных решений позволяет принимать решение без оценки последствий ошибок.

	Вероятность ошибочного решения для решающего правила (3.1)
	Р P		f x / D		dx P		x0		f x / D				dx
	ош 1		1			2						2	,			(3.11)
		x0
	для значений (3.8) получим условие минимума ошибочных решений
	dР	P f x / D P f x										/ D		0
	ош														,	(3.12)
	dx		1		0	1			2	0			2
					x0
	0			f		/ D1				P2
	или
				f	x	/ D				P		,				(3.13)
	.				0	2				1

тогда принимаем следующие решения:
x D , если		f x	/ D				Р
		0	1				2	;
		f x
1			/ D				Р
		0	2				1
x D		f x / D				Р
	, если		1				2
		f x / D
2						Р
			2				1

(3.14)

(3.15)

Соотношения (3.13) – (3.15) являются частным случаем метода

минимального риска при условии, что	С12	С21

Метод минимакса применим для ситуации, когда отсутствуют предварительные статистические данные о вероятности диагнозов D1 и D2. При этом выбирают значение х0 таким образом, чтобы при наименее благоприятных значениях Р1 («наихудший случай») потери, связанные с ошибочными решениями, были бы минимальными.

Исходя из условия Р2 = (1 - Р1), будем считать, что величина риска является функцией х0 и Р1,

								0
					f x / D	dx C (1 P )		x	f x / D.	dx
R(х	, Р ) C	21	P
0	1		1		1	12	1		2
				x
				0

(3.16)

Минимизируем риск, приравнивая нулю частные производные

				R		0;			R			0 .
			x		0				Р
								1
В результате получаем								f (x0 / D1 )						C12 (1 P1 )	,
								f (x0 / D2 )						C21P1
										0
				f x / D dx C						x		f x / D dx
C	21
						1		12						2 .
		x
		0

(3.17)

(3.18)

(3.19)

Решая уравнения (3.18) и (3.19) определяем х0 соотношением функций распределения, которые определяют площади условных вероятностей ошибок на рис. 3.1.

			х0		х0
	F (x0 / D1 ) f (x / D1 )dx;				F (x0 / D2 ) f (x / D2 )dx ;	(3.20)
	1 F (x0 / D1 )		С12	, или С21	1 F (x0 / D1 ) С12 F (x0	/ D2 ) . (3.21)
	F (x0 / D2 )
			С21

Зависимость (3.21) выражает

равенство условных рисков ошибочных решений.