Оглавление

Введение…….………………………….….…..…….………….………...……….. 4

1. Основные понятия теории вероятностей ……..…..………..………...…….	5
2. Классическая и геометрическая вероятности ……..……..…………....……	6

3.Условная вероятность ……..……..……………………………………..…….. 8

4.Схема Бернулли ……..……..…………..……………………………..…….. 11

5.Случайная величина ……..……..…………..…………………………...……. 14

6.Дискретная случайная величина ……..……….…..………….……….…….... 14

7.Непрерывная случайная величина ……..……..…………..……….......…….. 18

8.Моменты случайных величин и другие числовые характеристики …....... 24

9.Функция от случайной величины ……..………….…………..………..…….. 27

10.Двумерная случайная величина ……..…………....…………..………...…… 29

11.Двумерная дискретная случайная величина ……..…………..………...….. 29

12.Двумерная непрерывная случайная величина ……..………...………...…… 30

13.Числовые характеристики двумерных случайных величин ...………..……. 31

Библиографический список..…………….…………………….…………….….. 36

Приложение 1.	Таблица значений функции φ (x) …………..…….…………	37
Приложение 2.	Таблица значений функции F(x) …………..…….…………	38

Типовой расчет….………..………………………………….…………..………. 39

3

ВВЕДЕНИЕ

Теория вероятностей есть, в сущности, не что иное, как здравый смысл, сведенный к исчислению: она заставляет оценить с точностью то, что справедливые умы чувствуют как бы инстинктом, часто не умея отдать себе в этом отчета.

Пьер-Симон Лаплас, французский математик, физик и астроном

(XVIII–XIX в.)

Теория вероятностей – это математическая наука, изучающая закономерности случайных явлений, которые рассматриваются в абстрактной форме и в виде упрощенной схемы – математической модели. Предметом теории вероятностей являются математические модели случайных явлений. Под случайным явлением понимают явление, предсказать исход которого невозможно. Цель теории вероятностей – прогноз и контроль случайных явлений, ограничение области действия случайности.

Первые работы, в которых зарождались основные понятия теории вероятностей, появились в XVII веке и описывали азартные игры (игральные кости) с целью дать рекомендации игрокам: «Книга об игре в кости» (Дж. Кардано), «О расчетах в азартной игре» (Х. Гюйгенс), «О выходе очков при игре в кости» (Г. Галилей) и др. Становление теории вероятностей как математической науки связано с именем Я. Бернулли, который впервые теоретически обосновал накопленные ранее факты в книге «Искусство предположений» в начале XVIII века.

Дальнейшими успехами теория вероятностей обязана А. Муавру, П. Лапласу, К. Гауссу, С. Пуассону и др. В конце XIX – начале XX века теория вероятностей становится самостоятельной строгой математической наукой в основном благодаря русским математикам П. Л. Чебышеву, А. А. Маркову, А.М. Ляпунову.

ВXX веке особенно стоит отметить вклад академика А. Н. Колмогорова, установившего аксиоматику теории вероятностей.

Сейчас методы теории вероятностей широко применяются в различных областях: в математической статистике, теории надежности, теории массового обслуживания, теории связи, теории автоматического управления и т. д. Теория вероятностей служит для построения математических моделей при планировании и организации производства, анализе технологических процессов и т. п.

Впособии представлены теоретические сведения по основным разделам теории вероятностей: случайные события, одномерные и двумерные случайные величины; типовой расчет, включающий в себя задания по этим разделам, необходимые для студентов технических вузов.

4

1. Основные понятия теории вероятностей

Рассмотрим некоторый опыт со случайными исходами. Событием называется факт, который в опыте может произойти или не произойти. События обычно обозначаются заглавными буквами латинского алфавита, например, A,

B , H1 .

Если событие обязательно появляется в результате данного опыта, то оно называется достоверным, и будем обозначать егоW (его также называют

множеством допустимых исходов).

Если событие заведомо не может произойти в результате опыта, то оно называется невозможным, и будем обозначать его какÆ (также называют

пустым множеством).

К событиям чаще всего применяются следующие алгебраические опера-

ции.
Произведением (пересечением) событий A и B (обозначается A × B или
A Ç B ) называется событие C , которое происходит тогда и только тогда, когда
одновременно происходят события A и B .
События A и B называются несовместными, если не могут появиться
одновременно в одном опыте, т. е. A × B=	Æ.	A + B или
Суммой (объединением) событий	A и B (обозначается
A È B ) называется событие C , которое	происходит тогда, когда	происходит

либо событие A, либо B , либо оба вместе.

Событие A называется противоположным (дополнением) к событию A,

если оно происходит тогда и только тогда, когда не происходит событие A. Событие A влечет событие B (обозначается A Ì B ), если при наступ-

лении события A обязательно наступает событие B .

Пример. Производится опыт – бросание игральной кости. Рассматриваются события A – {выпадет четное число очков} и B – {выпадет не более че-

тырех очков}. Найти исходы событий C = A × B , D = A + B , A .

Решение. Возможные исходы опыта – выпадение одного, двух, …, шести очков. Тогда событие A составляют следующие исходы: выпадет два, четыре или шесть очков, событию B удовлетворяют исходы: выпадет одно, два, три, четыре очка. Следовательно, событие C – {выпадет два или четыре очка}, D

– {выпадет любое число очков, кроме пяти}, A – {выпадет нечетное число очков}.

Для описания степени возможности появления событияA в опыте вводится числовая функция P( A) , называемая вероятностью, которая удовлетворяет трем аксиомам:

1)P( A) ³ 0 – аксиома неотрицательности;

2)P(W) =1 – аксиома нормированности;

3)P( A + B) P=( A) + P(B) , если A и B несовместные – аксиома сло-

жения.

5

Вероятность обладает следующими свойствами:

–вероятность невозможного события равна нулю: P(Æ) = 0 ;

–вероятность любого события лежит в пределах от 0 до 1: 0 £ P( A) £1;

–вероятность противоположного события находят по формуле

P( A) =1- P( A) ;

–«бόльшему» событию соответствует бόльшая вероятность, т. е. если A Ì B , значит, P( A) £ P(B) ;

–для любых событий A и B справедливо соотношение

P( A + B) =P( A) + P(B) - P (A × B) (теорема о сложении вероятностей).

2.Классическая и геометрическая вероятности

Вопыте с равновозможными случайными исходами вероятность события A вычисляется как отношение числа исходовM , благоприятствующих собы-

тию A, к общему числу N всех возможных исходов (классическое определение вероятности)

P( A) = M / N .

На практике справедливость формулы классической теоретической вероятности P( A) подтверждается вычислениемстатистической вероятности, которую можно найти по формуле

P* ( A) = lim M * / N * ,

N*®¥

где в N * повторяющихся одинаковых испытаниях событие A наступило M * раз. Заметим, что теоретическая и статистическая вероятности удовлетворяют всем аксиомам и свойствам вероятности.

Пример. Из колоды 36 карт вытаскивается одна карта. Найти вероятности следующих событий: A – {карта окажется пиковым тузом}, B – {карта окажется королем}, C – {карта окажется червовой масти}.

Решение. В данном опыте общее число исходов равно количеству карт в колоде – N = 36 . Для события A благоприятствующее число исходов M =1 (в колоде один пиковый туз), следовательно, P( A) =1/ 36 . Для события B благоприятствующее число исходов M = 4 (в колоде четыре короля), следовательно, P( A) = 4 / 36 =1/ 9 . Для события C благоприятствующее число исхо-

дов M = 9 (в колоде четыре масти по девять карт в каждой), следовательно,

P(C) = 9 / 36 =1/ 4 .

6

При подсчете числа исходов часто пользуются понятиями и формулами комбинаторики.

Перестановкой из n элементов называется любой упорядоченный набор этих элементов. Число перестановок обозначается Pn и вычисляется по форму-

ле Pn = n!.

Размещением из n элементов по m называется любой упорядоченный набор m элементов, выбранных из совокупности n элементов. Число размеще-

ний обозначается Am		Am =	n!
	и вычисляется по формуле			.
n		n	(n - m)!

Сочетанием из n элементов по m называется любой неупорядоченный набор m элементов, выбранных из совокупности n элементов. Число сочета-

ний обозначается Cnm и вычисляется по формуле Cnm =	n!
		.
	m!(n - m)!

Пример. В урне находятся 8 шаров, среди которых 5 черных и 3 белых. Наудачу вынимают 4 шара. Найти вероятности событий A – {все вынутые шары окажутся черными}, B – {среди вынутых шаров окажутся 2 черных и 2 белых шара}.

Решение. В данном опыте общее число исходов равно количеству -все возможных комбинаций четырех шаров, выбранных из восьми шаров, т. е. чис-

4	8!	8 × 7 ×6	×5
лу сочетаний из восьми по четыре – N = C8	=	=		70. Для
	4!(8 - 4)! 4 ×3× 2 ×1

события A благоприятствующее число исходов равно количеству всевозможных комбинаций четырех черных шаров, выбранных из пяти черных шаров,

4	5!		5
иначе числу сочетаний из пяти по четыре– M = C5=	= =			5 , и
			1
	4!(5 - 4)!

P( A) = 5 / 70 =1/14 . Для события B благоприятствующее число исходов равно количеству всевозможных комбинаций двух черных шаров, выбранных из общего числа пяти черных шаров, умноженному на количество всевозможных комбинаций двух белых шаров, выбранных из общего числа трех белых шаров. В результате благоприятствующее число исходов

2

2

5!

3!

5

× 4

3

M = C5

×C3

=

×

=

×

30 , и P(B) = 30 / 70

= 3/ 7 .

1

2!(5 - 2)! 2!(3 - 2)! 2 ×1

Если число равновозможных исходов несчетно и представляет собой некоторое непрерывное множество, то применяется принцип геометрической вероятности. В данном случае опыт заключается в бросании точки в пределах множества допустимых исходов – области W . Тогда вероятность наступления события A определяется как вероятность попадания точки в подобласть A, соответствующая множеству исходов события A, и находится по формуле

7

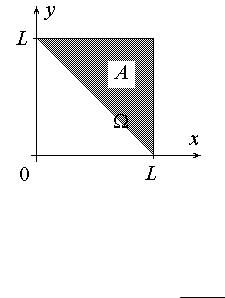
P( A) = μ(A) / μ(W) ,

где μ – длина, площадь, объем и т. д. в зависимости от размерности областей. Пример. Какова вероятность того, что сумма длин двух наудачу взятых

отрезков, длины каждого из которых равновероятно распределены на интервале (0, L) , будут больше L ?

Решение. Обозначим через x длину первого отрезка, через y – длину второ-

го. Длины выбираются наудачу из интервала (0, L) , следовательно, применяется гео-

метрическая вероятность. Множество W : {(x, y ) : 0 < x, y < L} – квадрат на ри-

сунке, множество A: {(x, y ) : x + y > L} – закрашенный треугольник.

Тогда вероятность события A – {сумма длин двух наудачу взятых отрезков, длины каждого из которых равновероятно распределены на интервале(0, L) ,

будут больше L } вычисляется по формуле P( A) =	μ(A)		S				1	L2		1
						2
	=				=				=		.
			S					2		2
	μ(W)						L

3. Условная вероятность

Для нахождения вероятности одновременного наступления событий A и B используется формула умножения вероятностей

P( A × B) P=( A) × P(B | =A) P(B) × P( A | B) ,

где P(B | A) – условная вероятность события B при условии, что событие A произошло (аналогично определяется P( A | B) ).

Пример. На связке пять ключей. К замку подходит только один из них. Ключи по очереди подбираются для открытия замка. Найти вероятность того, что ключ подойдет со второй попытки (событие A).

8

Решение.

Рассмотрим события A1 – {первый ключ не

подошел}, A2 –

{второй ключ

подошел}. Тогда P( A) = P(

P=(

A1 × A2 )

A1 ) × P( A2 | A1 ) , где

P(

P( A2 |

(один

A1 ) = 4 5 (четыре неподходящих ключа из пяти),

A1 ) =1 4

подходящий ключ из оставшихся четырех). Получаем P( A) =

4

×

1

=

1

.

5

4

5

Если наступление одного события не влияет на вероятность

появления

другого, то события называют независимыми. Необходимым и достаточным ус-

ловием	независимости событий A и B	является следующее	соотношение:
P( A × B)	P=( A) × P(B) .
Пример. Три стрелка независимо		друг от друга делают	по одномувы

стрелу, целясь в одну мишень. Вероятность попадания в мишень для первого стрелка равна 0,8 , для второго – 0,7 , для третьего – 0,6. Найти вероятности событий: A – {после стрельбы в мишени обнаружено две пробоины}, B – {после стрельбы в мишени обнаружено хотя бы одно попадание}.

Решение. Рассмотрим события A1 – {первый стрелок попал в мишень}, P( A1 ) = 0,8; A2 – {второй стрелок попал в мишень}, P( A2 ) = 0,7 ; A3 – {третий стрелок попал в мишень}, P( A3 ) = 0,6 . Также рассмотрим противополож-

ные события A1 – {первый стрелок не попал в мишень}, P( A1 ) =1 - 0,8 = 0, 2 ;

A2 – {второй стрелок не попал в мишень}, P( A2 ) =1- 0, 7 = 0,3; A3 – {третий стрелок не попал в мишень}, P( A3 ) =1 - 0, 6 = 0, 4 . Тогда событие A является суммой трех несовместных событий: {первый и второй попали, третий не по-

пал} – A1 × A2 × A3 , {первый и третий

попали, второй не попал} –

A1 × A2 × A3 ,

{второй

и третий

попали, первый не

попал} –

вероятность

A1 × A2 × A3 . Тогда

события

A:

P( A) = P(

A1 × A2 × A3 ) + P( A1 × A2 × A3 ) + P( A1 × A2 × A3 )=

= P( A1 ) × P( A2 ) × P( A3 ) + P( A1 ) × P( A2 ) × P( A3 ) + P( A1 ) × P( A2 ) × P( A3 ) = 0, 452.

События A1, A2 , A3 , A1 , A2 , A3 являются попарно независимыми, так как попа-

дание или промах одного из стрелков не влияет на меткость выстрела любого другого.

Для нахождения вероятности события B удобно рассмотреть противоположное событие B – {после стрельбы в мишени не обнаружено ни одного по-

падания}, т. е. {первый, второй и третий стрелки не попали} –

A1 × A2 × A3 . То-

гда P(

) = P(

Следовательно,

B

A1 × A2 × A3 ) P=( A1 ) × P( A2 ) × P( A3 ) = 0,024 .

P(B) =1 - P(

) =1 - 0,024 = 0,976 .

B

9

Пусть событие A может наступить только при появлении одного из событий H1 , H2 ,…, Hn , которые образуют полную группу – события H1 , H2 ,…,

n

Hn попарно несовместны друг с другом и åP(Hi ) =1. Тогда вероятность на-

i=1

ступления события A вычисляется по формуле полной вероятности

n

P( A) = åP(Hi ) × P( A | Hi ) ,

i=1

причем H1 , H2 ,…, Hn называют гипотезами.

Пример. При разрыве снаряда образуются крупные, средние и мелкие осколки в отношении 1: 3: 6 . При попадании в танк крупный осколок пробивает броню с вероятностью 0,9 ; средний – 0,3 ; мелкий – 0,1. Какова вероятность того, что попавший в броню осколок пробьет ее (событие A)?

Решение. Рассмотрим следующие гипотезы: H1 – {крупный осколок по-

пал в броню}, H2 – {средний осколок попал в броню}, H3 – {мелкий осколок попал в броню}. Вероятности гипотез рассчитываем, используя заданное соот-

ношение

образования

осколков1: 3: 6

:

P(H1 ) =

1

= 0,1,

1 + 3 + 6

3

6

P(H2 ) =

= 0,3,

P(H3 ) =

= 0,6 .

Заметим,

что

1+ 3 + 6

1 + 3 + 6

P(H1 ) + P(H2 ) + P(H=3 ) 0,1+ 0,3 + 0,6 =1. В задаче заданы условные веро-

ятности

пробивания

брони

каждым

:

осколкомP( A | H1 ) = 0,9 ,

P( A | H2 ) = 0,3, P( A | H3 ) = 0,1.

Тогда

P( A) = P(H1 ) × P( A | H1 ) +

+P(H2 ) × P( A | H2 ) + P(H3 ) × P( A=| H3 ) 0,1×0,9 + 0,3 ×0,3 + 0,6 ×0,1 = 0, 24

Если при тех же условиях событие A свершилось, то пересчет вероятностей гипотез производится по формуле Байеса

P(Hk | A) =	P(Hk ) × P( A | Hk )	, k =1, 2,..., n .
	n

åP(Hi ) × P( A | Hi )

i=1

Пример. Из 25 студентов группы 5 студентов знают все30 вопросов программы, 10 студентов выучили по 25 вопросов, 7 студентов – по 20 вопросов, трое – по 10 вопросов. Случайно выбранный студент ответил на задан-

10

ный вопрос (событие A свершилось). Какова вероятность того, что он из тех студентов, которые подготовили 10 вопросов?

			Решение. Рассмотрим следующие гипотезы: H1 – {вызван студент, кото-
рый выучил 30 вопросов},															P(H1 ) =														5								=				1		;		H2 – {вызван студент, который
																						25																5
выучил 25 вопросов}, P(H2 ) =																					10				=						2				;				H3						– {вызван студент, который вы-
																															5
																25
учил 20 вопросов}, P(H3 ) =																	7			;			H4									– {вызван студент, который выучил 10
													3			25
вопросов},							P(H4 ) =							. Заметим, что																									P(H1 ) + P(H2 ) + P(H3 ) + P(H4 ) =
										25
=	1	+		2	+	7			+	3= 1. Рассмотрим событие A – {вызванный студент ответит
5			5			25				25																																																		30
на заданный									вопрос}. Тогда							условные																	вероятности будут P( A | H ) =																													=1,
																																																						1					30
								25			5												20											2																	10					1
P( A | H2 ) =										=		, P( A | H3 ) =															=												, P( A | H4 ) =															=			. Найдем веро-
							30			6												30									3														30									3
ятность										события A																по																					формуле											полной				:	веро
			4															1										2								5						7					2		3			1			19
P( A) = åP(Hi ) × P(=A | Hi )																										× 1 +						×							+							×		+		×			=					. Вероятность
																5
					i=1																	5 6 25 3 25 3 25
того, что студент, ответивший на вопрос, оказался из тех, кто выучил всего де-
сять											вопросов,				находится																																	по											формуле
								P(H4 ) × P( A | H								4 )						3				×				1								1
P(H			4 | A) =																			25 3
										=					=									19																					.
																																						19
											P( A)
																						25
																4.							Схема Бернулли
			Пусть производится n независимых опытов, в каждом из которых собы-
тие A может появиться с одной и той же вероятностью p (вероятность «успе-
ха»). При этом q =1 - p называют вероятностью «неудачи», и такая последо-
вательность опытов называется схемой Бернулли. Тогда вероятность того, что в
n опытах событие A появится m раз, вычисляется по формуле Бернулли
																P (m) = C m pmqn-m .
																	n															n

11

Пример. Бланк программированного опроса состоит из четырех вопросов. На каждый вопрос даны три ответа, среди которых один правильный. Какова вероятность того, что методом угадывания студенту удастся выбрать, по крайней мере, три правильных ответа (событие A)?

Решение. В данной задаче число независимых испытаний – это число вопросов n = 4 . Вероятность «успеха» – это вероятность угадать правильный от-

вет в

каждом вопросе–

p =

1

,

следовательно,

вероятность «неудачи» –

1

2

3

q =1 -

=

. Рассмотрим события:

A – {студент угадал три правильных от-

3

3

1

вета},

A2 – {студент угадал четыре правильных ответа}. Для события A1 число

«успехов»

m = 3, для

события A2

число «успехов»

m = 4 .

Тогда

3

æ 1 ö3

æ 2 ö1

4

æ 1 ö4 æ 2 ö0

P( A) = P( A1 ) + P( A2 ) P4

(3) += P4 (4) C4

ç

÷=

ç

÷

+ C4

ç

÷ ç

÷

=

è

3 ø è

3 ø

è

3 ø è

3 ø

=

4!

2

+

=4!

1

4 × 2

+

1

=

1

. (По определению 0! =1).

3!(4 - 3)! 34

4!(4 - 4)! 34

81 81 9

При большом числе n опытов применяются приближенные формулы.

Теорема Пуассона. Пусть в схеме Бернулли n велико, а p близко к нулю,

тогда

λm

P (m) »

e-λ , где λ = np .

n

m!

Пример.

В пчелиной семье 4000 пчел. Вероятность заболевания в тече-

ние дня равна 0,001 для каждой пчелы. Найти вероятность того, что в течение дня заболеет более чем одна пчела (событие A).

Решение. Число независимых испытаний– это количество пчел n = 4000 . Вероятность «успеха» – это вероятность заболевания пчелы в течение дня p = 0,001, тогда λ = 4000 ×0, 001 = 4 . В данной задаче необходимо

рассмотреть обратное событие A – {в течение дня заболеет либо одна пчела,

либо ни

одна

пчела

не

заболеет}. Тогда

вычисляем

по формуле

Пуассона

P

(

= P

(0 )+ P

(1=)

40

e-4 +

41

e-4

= 0,09 . В

результате

получим

A

)

4000

4000

0!

1!

(

)

1 - 0,=09

0,91.

P (A) =1 - P= A

Локальная теорема Муавра-Лапласа. Пусть в схеме Бернулли n велико,

а p и q не близки к нулю, тогда

12

P

(m) »

1

φ (x ),

n

npq

x2

1

-

m

- np

где φ(x) =

e

2 , x =

. Значения функции φ(x) приведены в спе-

2π

npq

циальной таблице (см. Приложение 1). Заметим, что φ(-x) = φ(x) .

Интегральная теорема Муавра-Лапласа. Пусть в схеме Бернулли n ве-

лико, а p и q не близки к 0. Тогда вероятность того, что число успехов m бу-

дет заключено в пределах от m1 до m2 можно найти по приближенной формуле

P{m1 £ m £ m2 } » F(x2 )- F(x1 ),

где F(x) = 1

x

e

-

y2

dy – функция Лапласа, x = m1

- np ,

x = m2 - np .

2

1

2

2π ò0

npq

npq

Значения функции Лапласа приведены в специальной таблице (см. Приложение 2). Заметим, что F(-=x) -F( x) и при x > 4 имеем F(x) » 0,5 .

Пример. Монета подбрасывается 100 раз. Найти вероятность событий: A – {«орел» выпадет 50 раз}, B – {«орел» выпадет более 60 раз}.

		Решение. В данной задаче число независимых испытаний n =100 . Веро-
ятность				выпадения «орла»											в		каждом					броске p =										1		,				вероятность выпадения
																														2								1
							1												m - np											50 -100 ×
				q =													x =
«решки»										. Тогда																					=							2			0 .						По	таблице
							2
																				npq										100 ×			1		×		1
																														2								2	1 =
φ (0) = 0,3989 . Следовательно, P( A) = P																														(50)																	φ(0 )	0,08 . =
																						100																				1		1
																														100 ×													×
																																												2
								события B																															2
		Для																	имеем m1 = 60 и																							m2		=100 .				Тогда
	60 -100 ×							1								100 -100 ×									1
																									2
x	=						2					= 2 ,	x	2	=														= 10 . По таблице F(2) = 0, 4772
1					1		1														1		1
	100 ×					×										100 ×						×
							2
				2															2			2

иF(10) = 0,5 . Следовательно, P( B) = P(60 £ m £ 100) = F(10)- F(2) =

=0,5 - 0,4772 = 0,0228 .

13

5. Случайная величина

Случайной величиной называется числовая функция, которая каждому исходу опыта ставит в соответствие некоторое число. Случайные величины обозначаются как греческими буквами ξ , η , так и заглавными латинскими X , Y , при этом значения случайной величины будем обозначать строчными латинскими буквами x , y . Случайная величина X характеризуется функцией рас-

пределения F (x) , которая в каждой точке x определяется как вероятность со-

бытия { X < x} , т. е. F (x) = P{ X < x}. Функция распределения удовлетворя-

ет следующим свойствам:

–значения функции распределения лежат в пределах от 0 до 1: 0 £ F (x) £1;

–F (x) – неубывающая функция;

–поведение функции распределения на бесконечности:

F (-¥) lim F (=x) 0 , F (+¥)	lim F (=x) 1;
x®-¥	x®+¥

– вероятность попадания случайной величины X в интервал [x1 , x2 ) находит-

ся по формуле P{x1 £ X < x2 } F=(x2 ) - F (x1 ).

Будем рассматривать два типа случайных величин: дискретные и непрерывные случайные величины.

6. Дискретная случайная величина

Случайная величина называется дискретной, если ее значения представляют собой конечный (или счетный) набор чисел. Дискретная случайная величина X описывается законом распределения в виде следующей таблицы

X	x1	x2	…	xn
P	p1	p2	…	pn

В первой строке в возрастающем порядке расположены все возможные значения случайной величины, а во второй – вероятности того, что случайная вели-

чина примет то или иное значение:	pi = P{ X = xi } , i =1, 2,..., n . Заметим, что
n
å pi =1, и график функции	распределения имеет ступенчатый кусочно-
i=1

постоянный вид.

Случайная величина характеризуется неслучайными числовыми параметрами: математическим ожиданием и дисперсией. Математическое ожидание

14

дискретной случайной величины X характеризует среднее значение случайной величины и определяется по формуле

n

M (X )= åxi pi .

i=1

Математическое ожидание удовлетворяет следующим свойствам:

– если C = const , то M (C ) = C ;

– если a и b = const , то M (a × X + b) a ×=M (X ) + b ;

– для случайных величин X и Y справедливо соотношение

M (X + Y ) M=(X ) + M (Y ).

Дисперсия дискретной случайной величины X характеризует меру раз-

броса случайной величины относительно математического ожидания и определяется по формуле

n

D (X )= å(xi - M (X )2 pi .

i=1

Дисперсия удовлетворяет следующим свойствам:

– если C = const , то D (C ) = 0 ;

– если a и b = const , то D (a × X + b) = a2 × D (X ) ;

–D (X ) ³ 0 ;

–удобная формула вычисления дисперсии –

D (X ) = M (X 2 )- M 2 (X ).

Иногда для описания разброса случайной величины используетсясредне-

квадратическое отклонение, определяемое как

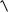
σX = D(X ) .

Пример. Студент выучил 12 из 20 вопросов к зачету. В билете – 3 вопроса. Составить закон распределения числа вопросов из билета, которые знает студент. Записать функцию распределения и построить ее график. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение.

Решение. Обозначим через X число вопросов в билете, которые знает студент. Тогда, случайная величина X принимает значения 0 , 1, 2, 3. Нахо-

15

8!

3

3! 8 - 3

)

!

8 ×7 ×6

дим

вероятности:

P (X = 0)

C8

=

(

=

=0,049 ,

=

C203

20!

20 ×19 ×18

3!(

20 - 3)!

12!

8!

1

2

1!(12 -1)=! 2!(8 - 2)!

12 ×8 × 7 ×3

P (X =1)

C12 ×C8=

=

=0, 295 ,

C203

20!

20 ×19 ×18

3!(20 - 3)!

12!

8!

C

2 ×

C

1

2! 12 - 2

!1! 8 -

1 !

12 ×11×8 ×3

P (X = 2)

(

)

(

)

12

8=

=

=

0,=463,

C203

20!

20 ×19 ×18

3!(20 - 3)!

12!

P (X = 3)

C123

=3!(12 - 3)!

=

12 ×11×10

=0,193 .

=

C203

20!

20 ×19 ×18

3!(20 - 3)!

Получаем закон распределения случайной величины X :

X

0

1

2

3

P

0,049

0, 295

0, 463

0,193

4

Проверим: å pi

= 0,049 + 0, 295 + 0, 463 + 0,193 =1.

i=1

Найдем числовые характеристики.

Математическое ожидание:

M ( X ) = 0 ×0,049 +1×0, 295 + 2 ×0, 463 + 3 ×0,193 =1,8 .

Дисперсия:

D (X ) = M ( X 2 ) - (M=( X ))2

02 ×0,049 +12 ×0, 295 + 22 ×0, 463 + 32 ×0,193 -

-1,82 = 0,644 .

Среднеквадратическое отклонение:

σ X = 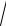0,644 = 0,802 .

Составим функцию распределения F (x):

при x £ 0 имеем F (x) = P{ X < 0} = 0 ;

при x £1 имеем F (x) = P{ X <1} =P{ X= 0=} 0,049 ;

16

при	x £ 2	имеем F (x) = P{ X < 2}= P{=X 0} + P{=X =1}
= 0,049 + 0, 295 = 0,344 ;
при x £ 3 имеем F (x) = P{ X < 3}			P={ X	0=} + P{ X =1} + P{ X = 2}
= 0,049 + 0, 295 + 0, 463 = 0,807 ;
при	x > 3 имеем F (x) = P{ X ³ 3}		0,049= + 0,295 + 0, 463 + 0,193 =1. В
результате функция распределения и ее график имеют вид
		ì0,		x £ 0;
		ï		0 < x £1;
		ï0, 049,
		F (x )= íï0,344,		1 < x £ 2;
		ï0,807,		2 < x £ 3;
		ï		x > 3.
		ï1,
		î

На практике часто встречаются следующие известные законы распределения дискретной случайной величины.

Биноминальное распределение имеет случайная величина X – число успехов в n испытаниях по схеме Бернулли, где вероятность находится по формуле Бернулли: P{ X = k} = Cnk pk qn-k , k = 0,1,..., n . Для биноминального за-

кона известны числовые характеристики M (X ) = n × p и D (X ) = n × p × q .

Распределение Пуассона имеет случайная величина Y – число успехов в схеме Бернулли при бесконечном числе испытанийn , где вероятность нахо-

	дится по формуле Пуассона P{Y = k} =	λk	e-λ , k = 0,1,... и λ > 0 – параметр
		k !

распределения Пуассона. Для закона Пуассона известны числовые характеристики M (Y ) = λ и D (Y ) = λ .

17

Геометрическое распределение имеет случайная величина Z – число испытаний в схеме Бернулли до наступления первого«успеха». Вероятности находятся по формуле: P{Z = k}= p × qk -1 , k =1, 2,..., а числовые характеристи-

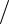ки вычисляются как M (Z ) =1 p и D (Z ) = q p2 .

7. Непрерывная случайная величина

Случайная величина называется непрерывной, если ее функция распределения непрерывна и кусочно-дифференцируема. Непрерывная случайная вели-

чина также характеризуется плотностью распределения вероятностей (плотностью распределения, плотностью вероятностей или просто плотностью)

f (x), связанной с	функцией распределения по	формулеf (x) = F ¢(x), или
x
F (x )= ò f ( y )dy .	Плотность распределения	удовлетворяет следующим
-¥
свойствам:

– неотрицательность: f (x) ³ 0;

– вероятность попадания случайной величины X в интервал [x1, x2 ] можно

x2

найти по формуле P{x1 £ X £ x2 } = ò f (x )dx ;

x1

+¥

– нормированность: ò f (x )dx =1;

-¥

– вероятность попадания в точку равна нулю: P{X = x0 } = 0 .

Математическое ожидание и дисперсия непрерывной случайной величи-

ны X имеют тот же смысл и те же свойства, что и дискретная случайная величина, а определяются формулами

¥

M (X )= ò xf (x )dx ,

-¥

¥	¥
D (X )= ò (x - M (X )2 f x=( dx)	ò x2 f (x )dx - M 2 (X ).
-¥	-¥

Среднеквадратическое отклонение непрерывной случайной величины X

определяется аналогично случаю дискретной случайной величины

σX = D(X ) .

18

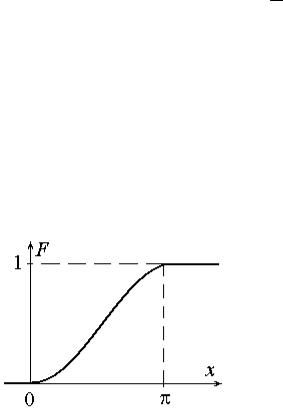
Пример.

Случайная

величинаX задана плотностью распределения

ì

0,

x £ 0,

ï

1

f (x) =

ï

sin x,

0 < x £ π,

Найти функцию распределения, вероятность по-

í

2

ï

0,

x > π.

ï

î

æ

π

;

π

ö

падания в интервал

ç -

÷

, математическое ожидание. Построить графики

3

2

è

ø

функции и плотности распределения.

x

Решение. Найдем функцию распределения как F (x )= ò

f ( y )dy :

-¥

x

при x £ 0 имеем F (x )= ò 0dy = 0 ;

-¥

0

x

1

1

1

при 0 < x £ π имеем F (x )= ò 0dy + ò

sin= ydy -

cos=y |0x

(1 - cos x);

2

2

2

-¥

0

x

0

π

1

-=1

при x > π имеем F (x )= ò 0dy + ò

sin ydy + ò0dy

cos y |0π =1.

2

-¥

0

π

2

ì0,

x £ 0;

ï

1

π

Функция распределения равна F (x )= íï

(1- cos x),

0 < x £

;

ï2

x > π.

2

ï1,

î

Графики функции распределения F (x) и плотности распределения f (x)

имеют вид

19

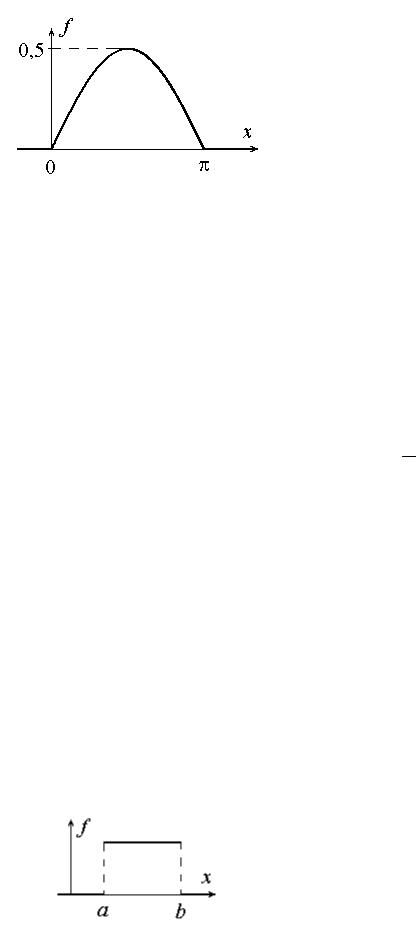
Находим математическое ожидание:

π

1

é

u = x

du = dx

ù

M (X

)= òx

sin xdx =

ê

1

1

ú

=

0

2

êdv = = sin xdx

v -

cos x

ú

2

π

ë

2

û

= -x

1

cos x

π

1

cos xdx =

æ

1

1

ö

1

π

|0

+

-ç

π

cos π

- 0 ×

cos 0

÷

+

sin x |0

=

2

ò0 2

2

2

2

è

ø

æ

p

ö æ 1

1

ö

π

æ 1

1

ö

π

-ç

-

- 0

÷ +

ç

sin π -

sin=

0 ÷

+ ç

×0 -

×0

÷

=

.

2

2

2

è

ø è 2

ø

2 è 2

ø

2

Находим	вероятность	попадания	в	æ	-
				ç
				è

π π ö

;интервал÷:

3 2 ø

ì

π

π

ü

æ π ö

æ

π

ö

1

æ

π ö

1

(1 - 0) =

1

P í-

< x <

ý=

F ç

÷

- F ç

-

÷=

ç1 - cos

÷

- 0

=

.

3

2

3

2

î

þ

è

2 ø

è

ø 2

è

2 ø

2

На практике часто встречаются следующие известные законы распреде-

ления непрерывной случайной величины.

Равномерное распределение определяется плотностью распределения

ì

1

, a £ x £ b;

f (x )= íï

b - a

ï

0, иначе

î

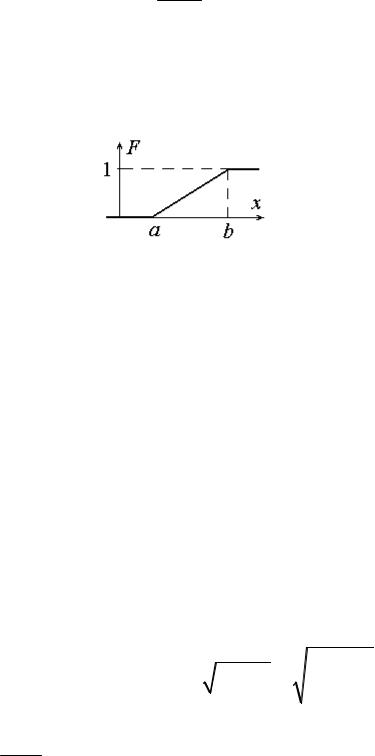
с параметрами a ¹ b и графиком функции плотности распределения

20

Функция распределения определяется соотношением

ì0, x < a;

ï x - a

F (x )= ïí , a £ x £ b;

ïb - a

ï 1, x > b

î

И график функции распределения имеет вид

	Числовые характеристики: M (X )=	a + b	и D (X	)=	(b - a)2		; вероят-
	2			12				x2 - x1
	ность попадания в интервал находится по формулеP{x £ X £ x					} =			,
	1			2				b - a

если a £ x1 £ x2 £ b .

Пример. Поезда метрополитена идут регулярно с интервалом5 минут. Пассажир спускается в метро и выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше минуты? Найти математическое ожидание и среднеквадратическое отклонение случайной величины X – времени ожидания поезда.

Решение. Случайная величина X равномерно распределена в интервале

[0;5],

следовательно,

плотность

распределения

запишется

в

виде

(

)

ì

1

,

0 £ x £

5;

(

)

0

+ 5

í

5

f

x

=

ï

Математическое ожидание M

X =

= 2,5;

ï

0,

x < 0, x > 5.

2

î

)

=

(5 - 0)2

среднеквадратическое

отклонение σ X =

D(X

=1, 47 ,

вероят-

12

ность

того,

что

ждать

пассажиру

придется

не

больше,

мин

P{0 £ X £1}

1 - 0

=

0,=2 .

5 - 0

21

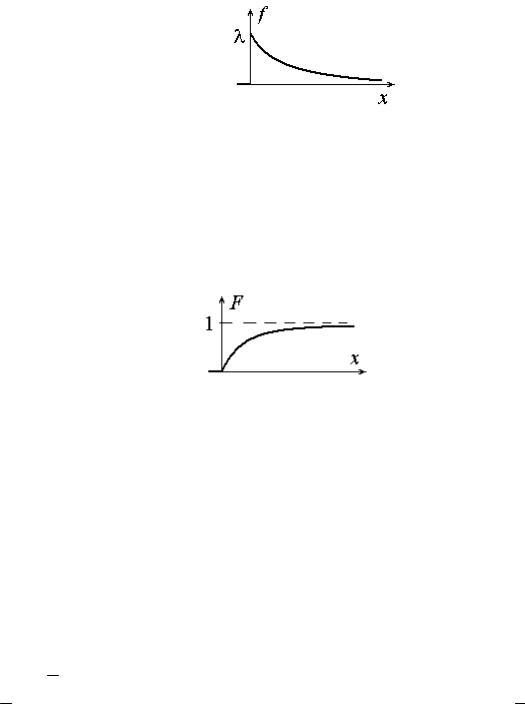
Показательное распределение определяется плотностью распределения

f(x )= ìíλe-λx , x ³ 0;

î0, x < 0

спараметром λ > 0 и графиком функции плотности распределения

Функция распределения определяется соотношением

ì 0, x < 0;

F (x )= íî1- e-λx , x ³ 0

И график функции распределения имеет вид

Числовые характеристики: M (X )=	1	и D (X	)=	1		; вероятность по-
	λ			λ2
падания в интервал находится по формуле P{x £ X £ x }					=e-λx1 - e-λx2 , если
x2 ³ x1 ³ 0.		1	2
Пример. Время безотказной работы		прибора	имеет показательное -рас

пределение с параметром λ =1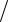80 (1/час). Найти вероятность того, что прибор не выйдет из строя в течение 100 часов (событие A).

Решение. Рассмотрим случайную величину T – время безотказной работы, распределенную по показательному закону с параметромλ =180 (1/час).

Чтобы прибор	не вышел из	строя в	течение100 часов, необходимо, чтобы
T >100 час. В	данной задаче	удобнее	найти вероятность противоположного

события A – {прибор выйдет из строя в течение100 часов}, т. е. T £100 час.

P (A) = P{0 £ T £100} = e0 - e-1,25 = 0,71. Тогда P (A) =1 - P (A) = 0, 29.

22

Нормальное распределение определяется плотностью распределения

f (x )=	1			e	-	(x-m)2
						2σ	2

σ 2π

спараметрами m и σ > 0 и графиком функции плотности распределения

Функция распределения определяется соотношением

		1			x	(y-m)2
F (x )=					ò e-		dy .
						2σ2
	σ		2π
				-¥

И график функции распределения имеет вид

Числовые характеристики: M (X ) = m и D (X ) = σ2 ; вероятность попа-

дания

в

[

1 2

]

находится

по

формул

интервалx ; x

P{x £ X £ =x }

Fæ x2 - m ö - Fæ x1

- m ö , где F(x) =

1

x

e

-

y2

dy ,

зна-

2

1

2

ç

÷

ç

÷

σ

σ

2π ò0

è

ø

è

ø

чения которой приведены в специальной таблице (см. Приложение 2). Заметим, что F(-=x) -F( x) и при x > 4 имеем F(x) » 0,5 . Вероятность отклонения от математического ожидания на величину не более d определяется по форму-

	{				}	ç	÷
ле P			X - m		< δ=	2Fæ	δ	ö . Вероятность отклонения от математического
						è σ ø

23

σ = 0,3.

ожидания на величину	не более3σ определяется поправилу трех сигм:
P{m - 3σ < X < m + 3σ}	= 0,997 .

Пример. Для исследования продуктивности определенной породы - до машней птицы измеряют диаметр яиц. Наибольший поперечный диаметр яиц представляет собой случайную величину, распределенную по нормальному закону со средним значением 5 см и среднеквадратическим отклонением 0,3 см. Найти вероятность того, что диаметр взятого наугад яйца будет заключен в границах от 4,7 см до 6, 2 см (событие A). Найти вероятность того, что отклонение диаметра взятого наугад яйца от среднего значения не превзойдет 0,15 см (событие B ). Найти интервал, в который диаметр яйца попадет с вероятностью 0,997 .

Решение. Рассмотрим случайную величину X – наибольший поперечный диаметр яиц, распределенную по нормальному закону с m = 5 и

Тогда P (A )= P{4,7 £ X £ 6, 2}

æ 6, 2 - 5 ö

æ 4,7 - 5 ö

Fç=

÷ - Fç

÷ =

0,3

0,3

è

ø

è

ø

= F(4)- F(-1) =F(4)+ F(1) =0,5 + 0,3413=

0,8413.

æ 0,15 ö

P (B )= P{

X - 5

< 0,15} =2Fç

÷= 2F(0,5

)

=2 ×0,1915 = 0,383 .

è

0,3 ø

интервал 5 - 3×0,3 < X < 5 + 3 ×0,3

Используя правило трех сигм, получаем

или X Î(4,1;5,9).

8. Моменты случайных величин и другие числовые характеристики

Начальным моментом порядка k

случайной величины X называется

математическое ожидание k -ой степени этой величины

αk

= M (X k ).

Для дискретной случайной величины начальный момент выражается суммой

n

αk = åxik pi ,

i=1

адля непрерывной случайной величины – интегралом

¥

αk = ò xk × f (x )dx .

-¥

24

В частности, математическое ожидание есть начальный момент первого порядка: α1 = M (X ).

Центральным моментом порядка k случайной величины X называется математическое ожидание величины (X - M (X )k

μk = M (X - M (X )k .

Для дискретной случайной величины центральный момент выражается суммой

n

μk = å(xi - M (X )k pi ,

i=1

адля непрерывной случайной величины – интегралом

¥

μk = ò (x - M (X )k × f (x )dx .

-¥

В частности, дисперсия есть центральный момент второго порядка:

μ2 = D (X ). Центральные моменты могут быть выражены через начальные моменты по формулам

μ= α			2	-α2	,
	2			1
μ= α	3	-3α		α +2α3		,
3			2	1	1

μ4 =α4 -4α3α1 +6α2α12 -3α14 .

Моменты более высокого порядка применяются редко. Моменты третьего и четвертого порядков применяются для нахождения таких числовых характеристик, как коэффициенты асимметрии и эксцесса.

Коэффициент асимметрии случайной величины X характеризует скошенность распределения и определяется по формуле

As = μ3 .

σ3X

Коэффициент эксцесса случайной величины X характеризует островершинность распределения и определяется по формуле

25

Ex = μ4 - 3.

σ4X

Для нормального закона распределения As = 0 и Ex = 0 ; остальные распределения непрерывной случайной величины сравниваются с нормальным. Если As > 0 , то правая часть кривой распределения более полога, As < 0 – сле-

ва более полога, As = 0 – распределение симметрично. Если Ex > 0 , то рас-

пределение более островершинное, чем нормальное, если Ex < 0 – распределе-

ние плосковершинное. Для дискретной случайной величины эти коэффициенты не используются.

Модой дискретной случайной величины X называется ее значение, принимаемое с наибольшей вероятностью по сравнению с двумя соседними значе-

ниями. Мода обозначается через M 0 (X ); для непрерывной случайной величи-

ны мода – это точка локального максимума плотности f (x).

Медианой непрерывной

случайной величины X называется значение

M e (X ), получаемое из соотношения

P

{

X < M

(X )

= P

{

X > M

(X

)

=

1

.

e

}

e

}

2

Иначе, медиану удобнее найти из уравнения

F (M e (X ) = 12 .

В частности, для равномерного закона M e (X )= a +2 b , для показательного – M e (X )= ln(2)λ , для нормального – M e (X ) = m . Для дискретных слу-

чайных величин медиана обычно не определяется.

Квантилью xp уровня p ( 0 < p <1) случайной величины X называется решение уравнения

F (xp ) = p .

26

9. Функция от случайной величины

Рассмотрим дискретную случайную величину X , заданную законом распределения

X	x1	x2	…	xn
P	p1	p2	…	pn

Функцией от дискретной случайной величиныX является новая дис-

кретная случайная величина Y = φ(X ) с законом распределения

Y	φ(x1 )	φ(x2 )	…	φ(xn )
P	p1	p2	…	pn

если все φ(xi ) (i =1,..., n) различны. Если какие-то два (или больше) значения

φ(xi )

и φ(x j ) (i ¹ j) оказались равны,

то эти столбцы объединяются,

и соот-

ветствующая вероятность будет pi

+ p j .

Пример. Дискретная случайная величина задана законом распределения

X

-

π

-

π

0

π

π

4

3

3

4

p

0,3

0,2

0,1

0,1

0,3

Найти закон распределения случайной величины Y = cos X .

Решение.

Найдем

значения

случайной

величиныY

для

всех

значений

æ

π ö

1

æ

π

ö

2

, cos(0) =1,

случайной величины X . Имеем: cos ç-

÷ =

, cos ç

-

÷

=

2

4

2

è

3 ø

è

ø

æ π ö

æ π ö

1

2

cosç

÷ =

,

cosç

÷ =

. В

результате

получаем

закон

распределения

2

2

è

4 ø

è 3

ø

дискретной случайной величины Y в следующем виде:

Y

1

2

1

2

2

p

0,6

0,3

0,1

Рассмотрим непрерывную

случайную

величинуX ,

заданную

плотно-

стью распределения f (x). Непрерывная случайная величина Y = φ(X ) (или

27

y = φ (x)) называется функцией от непрерывной случайной величины X , если

φ(x) – строго монотонная дифференцируемая функция. Плотность распреде-

ления g ( y ) непрерывной случайной величины Y определяется по формуле

g ( y) = f éψ( y )ù ×			ψ¢( y )	,
	ë	û
где ψ – функция обратная к φ .
Если функция y = φ (x) в	интервале всех возможных значений непре-
рывной случайной величины X	не	монотонна, то следует разбить интервал

всевозможных значений на промежутки монотонности, для каждого из них

найти плотности распределения g (y ), а			искомую	плотность распределения
представить в виде совокупности плотностей g (y ) на всех промежутках.
Числовые характеристики новой случайной величиныY = φ(X )							можно
вычислять и без нахождения плотности распределения g (y )
		+¥
M (Y )= M (φ( X )) = ò φ(x )f x(					dx)	,
		-¥
D (Y )= D (φ( X )=)	+¥	éφ(x )- M (Y		)ù2	f (x )dx .
	ò
		ë		û
	-¥
Пример. Случайная величина X равномерно распределена на интервале
(0, π) . Найти плотность распределения			вероятностей			случайной	величины

Y = ctg (X ), вычислить ее математическое ожидание.

Решение.

Плотность распределения случайной величины X

имеет вид:

f (x )=

1

,0 < x < π . Функция φ (x) = ctg (x) на интервале (0; π)

монотонно

π

убывает

и

имеет

производную. Найдем

обратную

функцию:

ψ ( y) = φ-1 = arcctg (y ) и ψ¢( y )= -

1

. Следовательно,

плотность

рас-

1 + y2

пределения

случайной

величиныY

будет

иметь

следующий:

вид

g ( y )=

1

×

1

, - ¥ < y < +¥ .

π

1 + y2

28

Вычислим	математическое							ожидание	случайной	величиныY :
+¥	+¥		1			1
M (Y )= ò y × g ( y )dy =ò		y ×		×				dy = 0 в	силу нечетности	подынте-
			π		1+ y		2
-¥	-¥

гральной функции (или симметричности распределения относительно нуля).

10. Двумерная случайная величина

Совокупность двух случайных величин (X ,Y ) рассматриваемых совме-

стно, называется двумерной случайной величиной (или системой двух случайных величин). Она описывается двумерной функцией распределения F (x, y ), кото-

рая	определяется	как	вероятность совместного	появления	двух событий
{X < x} и {Y < y}:		F (x, y ) = P{X < x,Y < y}. Двумерная функция распре-
деления удовлетворяет следующим свойствам:				в пределах0	доот 1:
–	значения функции		распределения лежат

0£ F (x, y) £1;

–F (x, y ) – неубывающая функция по обоим аргументам;

–поведение функции на отрицательной бесконечности:

F (x, -¥) lim F (x,=y) 0 , F (-¥, y )	lim F (=x, y) 0;
y®-¥	x®-¥

– связь с одномерной функцией распределения:

F (x, +¥) lim F (x,=y) F (x) , F (=+¥, y )	lim F (=x, y) F ( y) ; =
y®+¥	x®+¥

– поведение функции на положительной бесконечности:

F (+¥, +¥==) lim F (x, y) 1.

x, y®+¥

11. Двумерная дискретная случайная величина

Двумерная дискретная случайная величина описываетсязаконом распределения в виде матрицы

	Y	y1	…	yn
	X
	x1	p11	…	p1n
	…	…	…	…
	xm	pm1	…	pmn

29

Здесь x1 ,..., xm – всевозможные значения дискретной случайной величи-

ны X , y1 ,..., yn – всевозможные значения дискретной случайной величины Y ,

m n

pij = P{X= xi ,Y= y j }, i =1,..., m , j =1,..., n , причем åå pij =1.

i=1 j=1

Законы распределения составляющих X и Y запишутся в виде таблиц

n

где pix = å pij j=1

m

где p yj = å pij i=1

X	x1	x2	…	xm
P	p1x	p2x	…	pmx

(сумма вероятностей по i -ой строке), и

Y	y1	y2	…	yn
P	p1y	p2y	…	pny

(сумма вероятностей по j -ому столбцу).

Условным распределением вероятностей дискретной случайной величины

X при известном Y = y j			называется совокупность			условных				вероятностей
P{X = xi | Y = y j }, i =1,..., m , вычисляемых по формуле
P	{	X = x | Y y		j }	P{X = xi ,Y = y j }		pij
					=			.	=	=
							p jy
		i			P{Y = y j }
Аналогично определяется условное					распределение вероятностей					дискретной

случайной величины Y при известном X = xi .
Дискретные случайные величины X и Y являются независимыми,						если
их	условные	распределения	совпадают	с	,безусловнымит. .
P{X = xi | Y = y j } =P{Y = y j | X= xi } = P{X= xi ,Y= y j }.
	12. Двумерная непрерывная случайная величина
Двумерная непрерывная случайная величина(X ,Y )				описывается дву-
мерной	плотностью	распределения вероятностей f (x, y ),		связанной с		дву-

30

мерной				функцией		распределениявероятностей		по	формуле
f (x, y	)=	¶	2	F (x, y )		x	y
					, или F (x, y	)= ò du ò f (u,v dv) . Двумерная плотность
				¶x¶y		-¥	-¥

распределения удовлетворяет следующим свойствам:

–неотрицательность: f (x, y ) ³ 0 ;

–вероятность попадания двумерной случайной величины (X ,Y ) в область D

можно найти по формуле P{(x, y )Î D} = òò f (x, y )dxdy ;

D

+¥ +¥

– нормированность: ò dx ò f (x, y dy) =1;

-¥ -¥

– вероятности попадания в точку или прямую равны нулю:

P{X = x } = P{Y= y		}= P{=X x=,Y =y } 0;
0	0	0	0
– плотности распределения составляющих находятся по формулам
+¥		+¥
fX (x )= ò f (x, y dy)	и fY ( y )= ò f (x, y dx) .
-¥		-¥
Условная плотность распределения X при заданном Y определяется по
формуле
		f (x | y) =	f (x, y )	.
			fY ( y )

Аналогично определяется условная плотность распределения Y при заданном X .

Непрерывные случайные величины X и Y являются независимыми, если

их условные плотности	распределения совпадают с безусловными, т. .
f (x | y ) = fX (x) и f ( y |	x) = fY ( y ). Критерием независимости служит ра-

венство f (x, y) = fX (x)× fY (y ).

13. Числовые характеристики двумерных случайных величин

Математическое ожидание и дисперсия двумерной случайной величины

(X ,Y ) определяются парами чисел (M (X ), M (Y )) и (D (X ), D (Y )), кото-

рые имеют те же определения, характеристики и свойства, что и в одномерном случае. Для двумерной случайной величины (X ,Y ) важными характеристика-

31

ми являются корреляционный момент (ковариация) K (X ,Y ) и коэффициент корреляции rXY , которые определяются по формулам

K (X ,Y ) = M éë(X - M (X ))×(Y - M (Y ))ùû ,

rXY = K ( X ,Y ) ,

σ X σY

и описывают степень зависимости случайных величинX и Y . Корреляционный момент и коэффициент корреляции удовлетворяют следующим свойствам:

– удобная формула вычисления корреляционного момента –

K (X ,Y ) = M (X ×Y ) - M (X )× M (Y ),

где для двумерной дискретной случайной величины (X ,Y ):

M ( X ×Y ) = åxi × y j × pij ,

		i, j
а для двумерной непрерывной случайной величины (X ,Y ):
	+¥	+¥
M ( X ×Y )	ò	ò
		dx = xy × f (x, y dy) ;
	-¥	-¥

– если X = Y , то K (X , X ) = D (X ) и rXX =1;

– если X и Y – независимые случайные величины, то K (X ,Y ) = rXY = 0;

– коэффициент корреляции по модулю не превышает единицы: -1 £ rXY £1.

Если rXY = ±1, то случайные величины X и Y имеют линейную функциональную связь.

Случайные величины X и Y являются коррелированными, если rXY ¹ 0 ,

и некоррелированными, если rXY = 0. Отсюда следует, что если X и Y – корре-

лированные, значит, и зависимые. А если X и Y – независимые, то и некоррелированные.

Пример. Закон распределения дискретной двумерной случайной величины (X ,Y ) задан в таблице

32

Y	0	1	2
X
1	0,2	0,3	0,1
2	0,1	0,0	0,3

Найти законы распределения составляющих, условный закон распределения случайной величины X при Y = 2. Найти математическое ожидание, дис-

персию и коэффициент корреляции двумерной случайной величины (X ,Y ).

Решение. Составим законы распределения составляющих. Имеем

X

1

2

P

0,6

0,4

Y

0

1

2

P

0,3

0,3

0,4

Находим

условный

закон

распределения случайной величиныX при

Y = 2. Имеем

P

X =1,Y = 2

0,1

P{X =1| Y =

2}

= {

=

=

}

0, 25;

0, 4

P{Y

= 2}

P

X = 2,Y = 2

0,3

P{X = 2 | Y =

2}

=

{

=

=

}

0,75.

0, 4

P{Y = 2}

Получаем

X | Y = 2

1

2

P

0,25

0,75

Находим числовые характеристики.

Математические ожидания: M ( X ) =1×0, 6 + 2 ×0, 4 =1, 4 ;

M (Y ) = 0 ×0,3 +1×0,3 + 2 ×0, 4 = 1,1.

Дисперсии: D (X ) =12 ×0, 6 + 22 ×0, 4 -1, 42 = 0, 24 ; D (Y ) = 02 ×0,3 +12 ×0,3 + 22 ×0, 4 -1,12 = 0,69 .

Среднеквадратические отклонения: σ X = 0, 24 = 0, 49 ;

σY = 0,69 = 0,83.

Корреляционный момент:

K (X ,Y ) = 1×0 ×0, 2 +1×1×0,3 +1× 2 ×0,1 + 2 ×0 ×0,1 + 2 ×1×0,0 + 2 ×2 ×0,3 -

-1, 4 ×1,1= -0,16.

33

Коэффициент корреляции: r =	= -0,16	-0,39 .
XY	0, 49 ×0,83
Пример. Плотность распределения непрерывной двумерной случайной
величины имеет вид: f (x, y) = c (x + y),0 £ x £1;0 £ y £1.			Определить кон-
станту c и вычислить P{Y + X <1}. Установить,		зависимы	X и Y или нет.

Найти математическое ожидание, дисперсию и коэффициент корреляции двумерной случайной величины (X ,Y ).

Решение. Изобразим область определения двумерной случайной величины D : 0 £ x £1,0 £ y £1 и область G : x + y <1 в области определения.

+¥

+¥

f (x, y

dy) =1.

Находим

константу c

из

условияò dx ò

Имеем

-¥

-¥

1

1

1 æ

y2 ö

1

1

æ

1 ö

òdxòc (x + y )dy =1

Þ còç xy +

÷

dx =1

Þ cò

ç x +

÷dx =1

2

2

0

0

0 è

ø

0

0

è

ø

1

æ x2

1

ö

æ

1

1

ö

Þ c =1. Значит, плотность

Þ cç

+

x ÷

=1 Þ c ç

+

÷

=1

распреде-

2

2

2

2

è

ø

0

è

ø

видf (x, y) = (x + y ), 0 £ x £1;0 £ y £1.

ления

имеет

Тогда

1

1-x

1

æ

y

2 ö

1-x

P{Y + X <1} = òò f (x, y )dxdy = òdx ò (x + y)dy = òç xy +

÷

dx =

2

G

0

0

0

è

ø

0

1-x

1 æ

(1 - x)

2

ö

æ

x

2

x

3

(1 - x)

3

ö

1

1

1

1

1

òç x (1

- x) +

÷

dx = ç

-

-

÷

=

-

+

=

.

2

6

ç

÷

ç

2 3

÷

2 3 6 3

0 è

ø

0

è

ø

0

34

Исследуем X и Y на зависимость. Для этого найдем безусловные и условные плотности распределения.

+¥

1

1

fX (x )= ò f (x, y dy) = ò(x + y)=dy x +

, 0 £ x £1;

2

-¥

1

0

fY ( y )= y +

, 0 £ y £1.

2

f (x | y) =

f (x, y=)

x + y

¹ f X (x ); f ( y | x) =

f (x, y=)

x + y

¹ fY ( y ).

fY (y )

y +

1

f X (x )

x +

1

2

2

Так как условные плотности не совпадают с безусловными, следователь-

но,

X и Y – зависимые.

Найдем числовые характеристики. Заметим, что математические ожида-

ния, дисперсии и среднеквадратические отклонения X и Y совпадают. Нахо-

ожидание: M (X )=

1

æ

1 ö

7

дим

математическое

x ç x +

÷=dx

=

M (Y ). Дис-

ò0 è

2 ø

12

персия: D (X						)=			1				2 æ							1 ö							æ		7			ö		2	11			D (Y ). Среднеквадратичное
									ò		x					x +							dx -
													ç								÷						ç					=				=
																				2									12			÷			144
									0				è								ø						è					ø
отклонение							σ X				=						11		= σY .											Находим								корреляционный	момент
				1		1							12													7					7					-1
K (X ,Y ) = òdxòxy (x + y )dy -																												×					=					и коэффициент	корреляции
				0		0																			12				12						144
	-1			æ											ö						1
rXY =			:				11		×	=			11							-				.
				ç												÷
	144					12
				è							12				ø						11

35