алгебра / дополнительная лит-ра / А.П. Мул методичка

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра «Прикладная математика»

ОСНОВНЫЕ ЗАДАЧИ ПО МАТЕМАТИКЕ ЗА 1 СЕМЕСТР

Часть 1: Линейная алгебра. Векторная алгебра

Методические указания

Ростов-на-Дону 2011

1

Составители: Ф.Л. Абуев, А.П. Мул, Г.Ю. Рябых, Н.В. Фролова

Основные задачи по математике за 1 семестр. Часть 1: Линейная алгебра. Векторная алгебра: методич. указания. – Ростов н/Д: Издательский центр ДГТУ, 2011. – 10 с.

Методические указания содержат рекомендации по проведению практических занятий и задания для самостоятельной работы по общему курсу математики за первый семестр.

Предназначены для студентов очной и заочной форм обучения всех факультетов.

Печатается по решению методической комиссии факультета «Информатика и вычислительная техника»

© Издательский центр ДГТУ, 2011

2

a a ... a

11 12 1n

A

am1 am2 ... amn

Линейная алгебра

Матрицы и действия над ними

Определение: Матрицей называется прямоугольная таблица чисел. Числа aij называются

элементами матрицы, индекс i указывает номер строки, индекс j – номер столбца, на пересечении которых находится элемент.

Если матрица имеет вид строкm и столбцовn, то m n – называется размером матрицы. Если m n, матрица называется квадратной. Две матрицы одного размера называются равными, если равны их соответственные элементы. Если все элементы матрицы равны нулю, то она называется нулевой, если элементы, расположенные на главной диагонали, равны единице, а

остальные нулю – единичной.
Над матрицами проводят следующие операции:
1) Сложение.	Пусть	A (aij ),		B (bij )–		матрицы одного раз-
мера, тогда C A B (aij				bij ) cij .
1 2		1 5				0	3
Пример: A		B			C A B
3 4		2	1			1	5

2)Умножение матриц на число. Пусть A (aij ), R ,

тогда A ( aij )

1		2		;	2 ;	2		4
Пример: A	3	4				2A	6	8	.

3) Умножение матриц. Операция определяется для матриц вида A (aij )m p , B (Bij )p n , т.е. число столбцов первой матрицы должно быть равно числу строк второй матрицы. Произведением матриц A и B называется матрица C (cij )m n , элементы которой

Cij ai1 b1j ai2 b2 aip bpj

1		2	4		,	3		1
Пример: A	5	10	2			C	4	2	,
				2 3			7
								11 3 2

3

1 3 2 4 4 ( 7)	1 1 2 2 4 11	,	33		41
C A B			C A B	41	47
5 3 10 4 2 ( 7) 5 1 10 2 2 11
						2 2

Обратная матрица Определение: Определителем квадратной матрицы называется число, определяемое по правилу

1) Пусть A							a11					a12		, тогда её определитель
							a					a
								21				22
	A				a11	a12				a11 a22 a12 a21
					a a
					21		22
2) Пусть A – квадратная матрица n-го порядка. Тогда
				a		a		a						a	a			a a				a	a
| A|				11		12		13				a					a				a
					a a			a						22	23			21	23			21	22
				21		22		23				11		a	a		12	a a			13	a	a
				a a				a						32	33			31	33			31	32
				31		32		33

Аналогично можно найти определители квадратных матриц любого порядка.

Определение: Квадратная матрица A называется вырожденной, если ее определитель равен нулю. Если определитель матрицы отличен от нуля, матрица A называется невырожденной. Любая невырожденная матрица имеет обратную.

Определение: Обратной матрицей к A называют матрицу A 1 того же размера, удовлетворяющую условию A A 1 A 1 A E , где

E – единичная матрица. Матрица A 1

находится по формуле

A

11

A

21

... A

n1

1

1

A

A

... A

,

A

12

22

n2

A

A1n

A2n

... Ann

где Aij – алгебраические дополнения соответственных элементов

матрицы A.

Пример: Найти обратную матрицу

3		2	1
		1	2		,
A 1
	2	2	5

4

					3									2			1
	A								1				1				2						3 ( 9) 2 1 1 4 33;
									2					2			5
A11					1									2			9;
									2					5
	A21										2				1							12;
													2		5
A31							2							1						3;
															2
							1
	A12												1				2					1;
														2			5
	A32								3					1						7;
														2
									1

A22						3					1					17;
						2					5
A13					1					1					4;
							2
											2
A								3			2					2;
23									2
											2
A33					3					2					5,
					1					1
					1					9						12	3
A	1										1					17 7
				33														.
											4					2	5
																	Векторная алгебра

Координаты вектора – проекции этого вектора на оси координат. Пусть A(x1,y1,z1) и B(x2 , y2 ,z2 ) – точки. Тогда вектор

AB (x2 x1, y2 y1,z2 z1).

Пример: A(1,2, 1); B(2,5,1); AB (2 1,5 2,1 1) (1,3,2)

5

Сумма векторов

Если a (ax,ay,az ), b (bx,by,bz ),

то a b (ax bx,ay by,az bz )

Пример: a (2,3,5), b (4,1,6), a b (2 4,3 1,5 6) (6,4,11)

Умножение на число

a ( ax, ay, az ) ( ax, ay, az )

Пример: 5a (10,15,25),

2a 3b 2(2,3,5) 3(4,1,6), 2a 3b (16,9,28)

Длина вектора

a (ax )2 (ay )2 (az )2

Пример: a (3,4,5), a 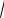32 42 52 50 52.

Скалярное произведение

	Обозначение: ab
						b		cos
	Определение: ab		a
	Формула вычисления:
	a (ax,ay,az ), b (bx,by,bz );
	a b (ax bx ay by az bz ).
Пример: a (4,5,2),	b (3,6, 1),	a b (40).

Геометрическое приложение

cos ab a b

Пример:a (2, 1,2),b (4,5,3),

a b 2 4 1 5 2 3 9, a 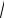22 12 22 9 3,

						9			3
b		42 52 32	5	2 , cos( )				cos( )
						3 5 2		5 2

Пример: a (4,8,1),

b ( 2,2,1),a b 4 ( 2) 8 2 1 9, b 4 4 1 3.

6

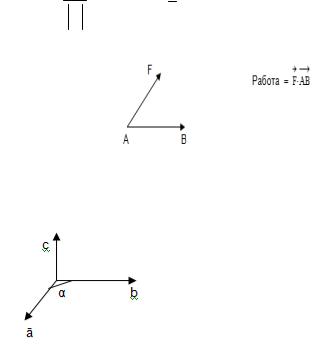
np a ab , np a 9 3 b b b 3

Механическое приложение

Пример: F (4,5,1),

AB (7,8, 3).

Работа 4 7 5 8 3 65(ед.работы)

Векторное произведение

Обозначение: a b c

Определение:

1.c a

и c b ; 2.

c

a

b

sin ;

3. a,b,c правая тройка.

k

i

j

ay

Формула вычисления: a b

ax

az

by

bx

bz

Пример:

a (2,4,1),

b (3, 1,5),

k

i

j

4

1

a b

2

i(20 1) j(10 3) k( 2 12) 21i 7j 14k

3

1 5

Приложение векторного произведения

1

S

a b

2

Пример: A(1,1,2),

B(1,2, 1),

C(2,1,3)

7

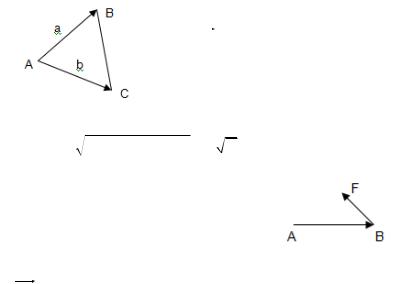
a AB (0,1, 3)
b AC (1,0,1)
				k
		i	j
a			1
	b 0			3 i 3j k (1, 3, 1)
			0	1
		1

S ABC 21 12 ( 3)2 ( 1)2 12 11

Момент силы					M AB F
Пример:			A (1,2,3),			B (1, 1,5),		F 2i 5j k
AB (0, 3,2),						F (2,5, 1),
				k
	i		j
		3
M	0			2	i(3 10) j( 4) 6k 7i 4j 6k ( 7,4,6)
	2		5	1

МоментM ( 7,4,6).

Смешанное произведение Определение: (a b)c

Обозначение:(a b)c abc

												ax	ay	az
													by
Формула вычисления:										abc		bx		bz
													cy
												cx		cz
Пример:
a (2,0,1), b (1, 1,0),													c (1,1,4),
				2		0	1
					1	1	0		2( 4) 1(1 1) 6
	abc
					1	1	4

8

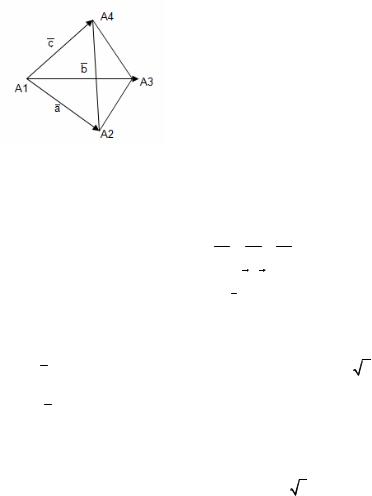
Приложение смешанного произведения

			Vnup	1	Vnap
Vnap	abc
				6

Пример: A1 (1,1,2), A2 (1,2, 1), A3 (3,1,4), A4 (5,4,8)

1.a A1A2			(0,1, 3)
b A1A3 (2,0,2)
c A1A4		(4,3,6)
	0	1	3
		0	2
abc 2				(12 8) 3 2 3 22
		3	6
	4

2. Vnup	1					1	22	11
	6		abc			6		3

11

Vnup 3 (куб. ед.)

Условие коллинеарности векторов: x1 y1 z1 . x2 y2 z2

Условие перпендикулярности векторов: a b 0.

Условие компланарности векторов: abc 0 .

1. Найти длину вектора:			Задания:
	a	(2;1; 2). Ответ: 3;			(5i;3j; 4k). Ответ: 5		.
а)			б)			2
				b

2.Найти скалярное произведение векторов:

1)a (1;3;5), b ( 2;1;4). Ответ: 21;

2)	a	(3i j 4k),			(2i 4j 3k). Ответ: -10.
				b
3.		Найти угол между векторами:					3
1)	a (2; 1;2),b (3;5;4). Ответ: cos								;
			5				2

2)a (7;5;1),b (3; 4; 1). Ответ: 90o.

9

4.Найти векторное произведение векторов:

1)a (3;4;5), b ( 2;1;3). Ответ: (7, -19, 11);

2)a (3i 4j 5k),		(2i 2 j k).
	b

Ответ: (6,-7,-2).

5. Найти площадь параллелограмма, построенного на векторах

a(1;1;1)и b (0;2;5). Ответ: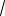38.

6.Найти площадь треугольника ABC, где A (1;1;2);

	B (1;2; 1);	C (2;3;4). Ответ:	74	.
			2

7. Найти смешанное произведение векторов:

a(1;1;3);b (1;2; 1); c (2;3;5). Ответ:3.

8.Найти объём пирамиды ABCD, где A (1;1;0);; B (1;2;3);

C (2;3;4);; D (4;6; 1). Ответ: 5/3.

Редактор А.А. Литвинова

________________________________________________________

В печать 28.11.2011.

Объем 0,62 усл.п.л. Офсет. Формат 60x84/16.

Бумага тип №3. Заказ № Тираж 50 экз. Цена свободная

________________________________________________________

Издательский центр ДГТУ Адрес университета и полиграфического предприятия:

344000, г. Ростов-на-Дону, пл. Гагарина, 1.

10