
лабораторка
.docФедеральное агентство по образованию
ГОУ ВПО «Омский государственный педагогический университет»
Лабораторная работа
Нахождение минимальных и максимальных путей на орграфах
Вариант 10
Выполнила:
студентка 31 группы
факультета информатики
Перменева М. С.
Проверила:
Титова Г.М.
Омск 2012
Задание 1. По заданной матрице весов Ω графа G найти величину минимального пути и сам путь от вершины s=x1 до вершины t=x7 по алгоритму Дейкстры, а затем величину максимального пути и сам путь между теми же вершинами.
Нахождение величины минимального пути
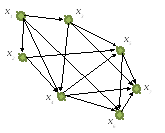
![]()

Этап 1. Нахождение длины кратчайшего пути.
Шаг
1.
Т.к. d(s)=0*,
то полагаем, d(x1)=0*,
X=x1,
d(x2)=d(x3)=d(x4)=d(x5)=d(x6)=
d(x7)=
![]()
Шаг 2. Множество вершин, непосредственно следующих за X= х1 с временными метками
S ={х2, х3, x4, х6}. Пересчитаем временные метки этих вершин:
d(x2)=min{![]() ,0*+7}=7
,0*+7}=7
d(x3)=
min{![]() ,0*+19}=19
,0*+19}=19
d(x4)=
min{![]() ,0*+20}=20
,0*+20}=20
d(x6)=
min{![]() ,0*+15}=15
,0*+15}=15
Шаг
3.
min{x2,x3,x4,x5,x6,x7}=min{7,19,20,![]() ,15,
,15,![]() }=7*=x2,
тогда
X=x2
}=7*=x2,
тогда
X=x2
Шаг 4. т.к. х2≠х7, то возвращаемся ко второму шагу.
2-я итерация
Шаг 2. S ={x4, х5}. Пересчитаем временные метки этих вершин:
d(x4)= min{20,7*+11}=18
d(x5)=
min{![]() ,7*+6}=13
,7*+6}=13
Шаг
3.
min{x3,x4,x5,x6,x7}=min{19,18,13,15,![]() }=13*=x5,
тогда
X=x5
}=13*=x5,
тогда
X=x5
Шаг 4. т.к. х5≠х7, то возвращаемся ко второму шагу.
3-я итерация
Шаг 2. S ={x6, х7}. Пересчитаем временные метки этих вершин:
d(x6)= min{15,13*+5}=15
d(x7)=
min{![]() ,13*+15}=28
,13*+15}=28
Шаг 3. min{x3,x4,x6,x7}=min{19,18,15,28}=15*=x6, тогда X=x6
Шаг 4. т.к. х6≠х7, то возвращаемся ко второму шагу.
4-я итерация
Шаг 2. S ={х7}
d(x7)= min{28,15*+14}=28
Шаг 3. min{x3,x4,x7}=min{19,18,28}=18*=x4, тогда X=x4
Шаг 4. т.к. х4≠х7, то возвращаемся ко второму шагу.
5-я итерация
Шаг 2. S ={x7}
d(x7)= min{28,18*+13}=28
Шаг 3. min{x3,x7}=min{19,28}=19*=x3, тогда X=x3
Шаг 4. т.к. х3≠х7, то возвращаемся ко второму шагу.
6-я итерация
Шаг 2. S ={x7}
d(x7)= min{28,19*+16}=28
Шаг 3. min{x7}=min{28}=28*=x7, тогда X=x7
Шаг 4. т.к. х7=t=х7, конец первого этапа.
Этап 1. Построение кратчайшего пути.
Шаг 5. S={x3,x4,x5,x6}
d(X)=28≠d(x3)+w(x3,x7)=19+16=35
d(X)=28≠d(x4)+w(x4,x7)=18+13=31
d(X)=28=d(x5)+w(x5,x7)=13+15=28
d(X)=28≠d(x6)+w(x6,x7)=15+14=19
Включаем дугу (х5,х7) в кратчайший путь Х=х5.
2-я итерация
Шаг 5. S={х2,x3,x4}
d(X)=13=d(x2)+w(x2,x5)=7+6=13
d(X)=13≠d(x3)+w(x3,x5)=19+9=28
d(X)=13≠d(x4)+w(x4,x5)=18+8=26
Включаем дугу (х2,х5) в кратчайший путь Х=х5.
3-я итерация
Шаг 5. S={х1}
d(X)=7=d(x1)+w(x1,x2)=0*+7=7
Включаем дугу (х1,х2) в кратчайший путь Х=х1.
Шаг 6. Х=s=х1, завершение второго этапа.
Итак, кратчайший путь от вершины х7 построен. Его длина (вес) равна 28, сам путь образует следующая последовательность дуг: µ=(х1,х2)-(х2,х5)-(х5,х7).
Нахождение величины максимального пути
![]()

Этап 1.
Задание 2. По заданной матрице весов Ω графа G найти минимальный путь по алгоритму Беллмана-Мура между начальной вершиной s=x1 и конечной вершиной t=x6.
![]()

Этап 1.
Шаг 1. X=x1, d(x1)=0, d(xj)=∞, j= , Q={ x1}
Шаг 2. X=x1, Q=Q\{x1}=Ø. Пусть S – множество вершин, непосредственно достижимых из вершины Х. S={x2,x3,x4}
d(x2}=min{∞,0+6}=6. 6<∞? Да. Q={x2}, x2 надо было поставить в конец очереди, но Q было пусто, поэтому конец очереди совпал с началом.
d(x3}=min{∞,0+11}=11. 11<∞? Да. Q={x2,x3}.
d(x4}=min{∞,0+5}=5. 5<∞? Да. Q={x2,x3, x4}.
Шаг 3. Q=Ø? Нет. Переход на начало второго шага.
2-я итерация
Шаг 2. X=x2, Q=Q\{x2}={x3,x4}. S={x4,x5,x6}
d(x4}=min{5,6+6}=5. 5<5? Нет.
d(x5}=min{∞,6+7}=13. 13<∞? Да. Q={x3,x4,x5}.
d(x6}=min{∞,6+6}=12. 12<∞? Да. Q={x3,x4,x5,x6}.
Шаг 3. Q=Ø? Нет. Переход на начало второго шага.
3-я итерация
Шаг 2. X=x3, Q=Q\{x3}={x4,x5,x6}. S={x2,x5}
d(x2}=min{6,11-5}=6. 6<6? Нет.
d(x5}=min{13,11+6}=13. 13<∞? Да. Q={x5,x4,x6}.
Шаг 3. Q=Ø? Нет. Переход на начало второго шага.
4-я итерация
Шаг 2. X=x5, Q=Q\{x5}={x4,x6}. S={x6}
d(x6}=min{12,13+7}=12. 12<12? Нет. Q={x4,x6}.
Шаг 3. Q=Ø? Нет. Переход на начало второго шага.
5-я итерация
Шаг 2. X=x4, Q=Q\{x4}={x6}. S={x6}
d(x6}=min{12,13+0}=12. 12<12? Нет. Q={x6}.
Шаг 3. Q=Ø? Нет. Переход на начало второго шага.
6-я итерация
Шаг 2. X=x6, Q=Q\{x6}=Ø. S=Ø
Шаг 3. Q=Ø? Да. Конец первого этапа. Найдены минимальные расстояния до всех вершин от первой. Эти расстояния таковы: d(x2)=6, d(x3)=11, d(x4)=5, d(x5)=13, d(x6)=12.
Этап 2.
Шаг 4. Полагаем X=x6. Пусть S – множество вершин, непосредственно предшествующих Х. S={x2,x4,x5}.
d(X)=d(x6)=12=6+6=d(x2)+w(x2,x6),
d(X)=d(x6)=12≠5+5=d(x4)+w(x4,x6),
d(X)=d(x6)=12≠13+7=d(x5)+w(x5,x6).
Включаем дугу (x2,x6) в кратчайший путь Х=х2. Возвращаемся на четвертый шаг.
2-я итерация
X=s? Нет.
S={x1,x3}.
d(X)=d(x2)=6=0+6=d(x1)+w(x1,x2),
d(X)=d(x2)=6=11-5=d(x3)+w(x3,x2).
Включаем дугу (x3,x2) в кратчайший путь Х=х3.
3-я итерация
X=s? Нет.
S={x1}.
d(X)=d(x3)=11=0+11=d(x1)+w(x1,x3),
Включаем дугу (x1,x3) в кратчайший путь Х=х1.
4-я итерация
X=s? Да. Задача закончена. Искомый кратчайший путь от вершины x1 до вершины x6 имеет вес равный 12 и состоит из следующих дуг: (x1,x3)-(x3,x2)-(x2,x6).
