Для студентов / Лекции / (2)ВЕД / (9)Електромагнітні потенціали

9. Електромагнітні потенціали

Обговорюючи властивості рівнянь Максвела, ми відмічали, що вона представляють собою систему 8-ми взаємно-залежних рівнянь для 6-ти змінних – компонентів напруженості електричного і магнітного полів. Для побудови їх рішень, таким чином, є бажаним перейти до інших змінних, які б задовольняли більш простим за структурою рівнянням. В цьому розділі ми покажемо, що такими змінними є електромагнітні потенціали. Останні узагальнюють поняття скалярного потенціалу в електростатиці і векторного потенціалу в магнітостатиці. Детально розглянемо властивості електромагнітних потенціалів і побудуємо для них рівняння.

а) Означення електромагнітних потенціалів

Третє рівняння Максвела (див. (6.19)) для напруженості магнітного поля є справедливим для всіх , тому допустимо представити у вигляді:

, (9.1)

де , як і раніше, будемо називати векторним потенціалом. Оскільки, рівняння виконується тотожньо, то тим самим задовольняється і третє з рівнянь Максвелла. Згідно означення (9.1), є полярним вектором.

Підставимо тепер вираз (9.1) для в друге з рівнянь Максвела: . Після тривіальних перетворень ми приходимо до рівняння

, (9.2)

яке також виконується для всіх . Звідси випливає, що векторне поле , яке стоїть під знаком , в області є потенціальним: . Звідси випливає, що

, (9.3)

де - скалярний потенціал електричного поля. Формули (9.1) і (9.3) визначають перехід від напруженостей електричного і магнітного полів до нових змінних – електромагнітних потенціалів і . Завдяки такому переходу двоє рівнянь Максвела, друге і третє, задовольняються тотожньо.

б) Рівняння для електромагнітних потенціалів

Підставимо тепер вирази (9.1) і (9.3) для напруженостей електромагнітного поля в перше і четверте рівняння Максвела. Таким шляхом ми приходимо до наступної системи взаємозв’язаних рівнянь для і :

:

.

Враховуючи стандартну тотожність , а також означення оператора Лапласа , отримані рівняння можна переписати у вигляді:

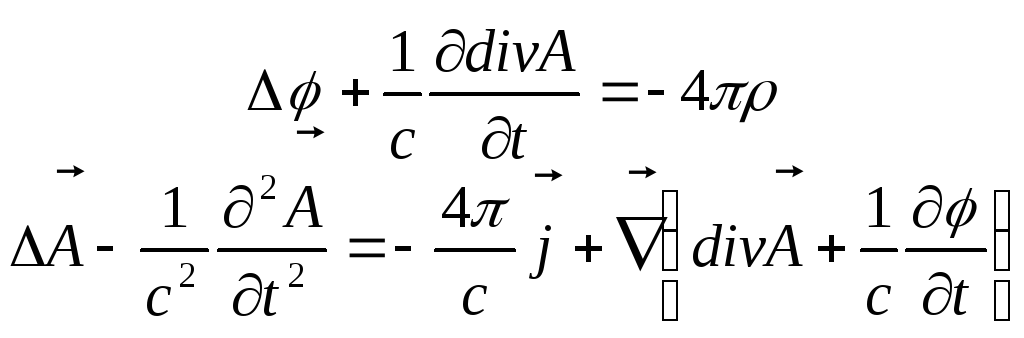. (9.4)

Бачимо, що перехід до електромагнітних потенціалів дозволяє нам зразу ж отримати чотири рівняння для чотирьох змінних: (). Проте, несиметричність цих рівнянь відносно скалярного потенціалу і компонентів векторного потенціалу є їх слабкістю. Нижче буде показано, що електромагнітні потенціали можна підкорити так званій калібрувальній умові Лоренца:

. (9.5)

При виконанні цієї умови рівняння (9.4) переходять в неоднорідні хвильові рівняння для і :

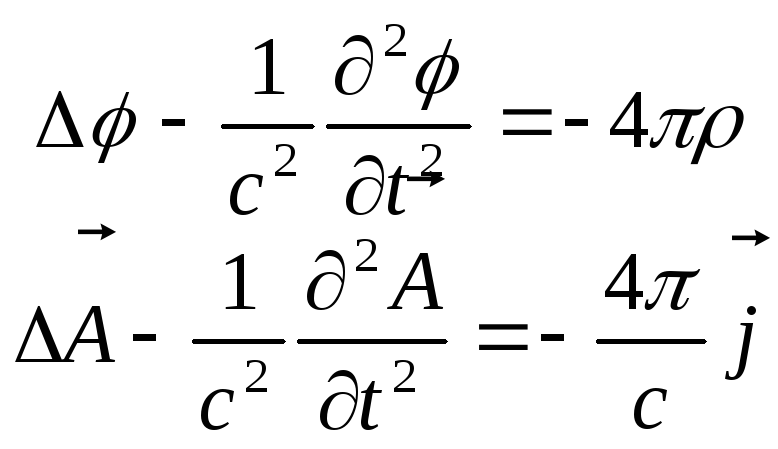. (9.6)

Через рівняння зв’язку (9.5) вони не є незалежними, але умова (9.5) не є обтяжливою і розв’язки рівнянь (9.6) можна будувати незалежним чином.

Дійсно, нехай . Функція задовольняє однорідному хвильовому рівнянню

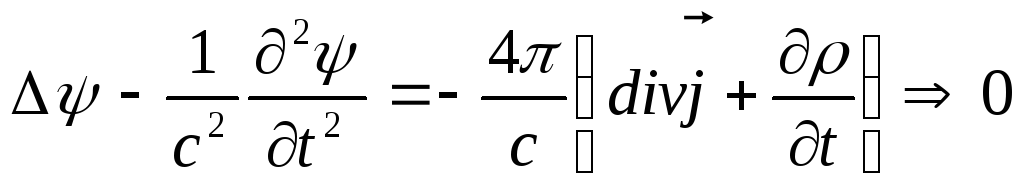, (9.7)

яке можна отримати, застосувавши оператори і до першого і другого рівнянь відповідно і утворивши їх суму. На останньому кроці ми використали закон збереження заряду (7.13). Це означає, що не залежить від конкретного розподілу зарядів і токів. Нижче буде показано, що тривіальним перенормуванням електромагнітних потенціалів функцію , взагалі, можна покласти рівною нулю.

Зазначимо, що з (9.5) і (9.6) випливає, що тільки три змінні з чотирьох () є незалежними. Цей висновок повністю узгоджується з тим, що був зроблений в розділі 7(г).

. в) Неоднозначність електромагнітних потенціалів і

Векторний потенціал, який визначає напруженість магнітного поля згідно (9.1), стоїть під знаком . Оскільки , це означає, що модифікований векторний потенціал

(9.8)

буде приводити до того ж самого значення . У зв’язку з цим ми говоримо, що електромагнітні потенціали і є еквівалентними (), якщо .

Визначимо тепер ступінь неоднозначності скалярного потенціалу . Підставимо в вираз значення модифікованого потенціалу . Як результат, отримуємо: . Для того, щоб і співпадали (), необхідно скалярний потенціал модифікувати наступним чином:

. (9.9)

Неоднозначність у визначенні електромагнітних потенціалів не вносить в електродинаміку ніяких непорозумінь. Справа в тому, що і не є експериментально вимірюваними величинами. Такими є тільки напруженості і електричного і магнітного полів. Саме вони пов’язані з силами, які діють на заряди токи і допускають пряме експериментальне визначення.

Таким чином, в теорії електромагнітного поля можна користуватись довільними потенціалами і , якщо вони належать до класу еквівалент-

ності з потенціалами і :

(9.10)

де - довільна скалярна функція. Таке свавілля в означенні електромагнітних потенціалів широко використовується в їх різноманітних застосуваннях.

Відзначимо один принциповий момент: закон збереження заряду є прямим наслідком неоднозначності електромагнітних потенціалів.

г) Калібрувальна умова Лоренца

Покажемо, що підходящою модифікацією електромагнітних потенціалів ми завжди можемо задовольнити калібровочній умові Лоренца. Нехай потенціали і задовольняють співвідношенню:

.

В той же час, перехід до еквівалентних потенціалів може привести до втрати цієї властивості:

.

Підставляючи сюди замість і їх вирази, які даються формулами (9.8) і (9.9), для функції ми отримуємо рівняння:

, (9.11)

яке за своєю структурою співпадає з рівняннями (9.6) для електромагнітних потенціалів. Це означає, що підбір підходящої функції не є принципово новою задачею. Інакше кажучи, ми можемо без зайвих утруднень будувати розв’язки рівнянь (9.6), розглядаючи їх як незалежні. В разі потреби до потенціалів і , отриманих таким шляхом, завжди можна додати внески від функції , які задовольняють рівнянню (9.11). У такий спосіб ми отримуємо потенціали, які узгоджуються з рівняннями (9.6) і калібрувальною умовою (9.5). Оскільки модифікація електромагнітних потенціалів за допомогою функції не позначається на значеннях напруженостей електричного і магнітного полів, ми можемо в подальшому користуватись і не модифікованими потенціалами.

Зазначимо, що за своїм смислом калібрування електромагнітних потенціалів є подібним до калібрування термометра: треба вибрати одиницю вимірювання температури і положення нуля на шкалі. Зрозуміло, що це можна зробити безліччю способів.

д) Кулонівське калібрування

Прикладом другого типу калібрування електромагнітних потенціалів є кулонівське калібрування:

. (9.12)

В цьому випадку система рівнянь (9.4) для потенціалів переходить у

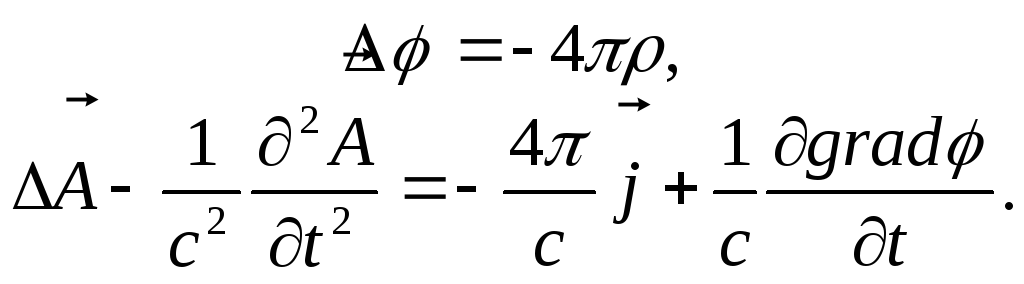(9.13)

Назва цього типу калібрування походить від того, що скалярний потенціал

в (9.13) задовольняє рівнянню Пуассона, яке має місце для статичного кулонівського поля зарядів. До речі, рівняння для потенціалів () відповідають їх кулонівському калібруванню. Для забезпечення калібрувальної умови (9.12) функція потрібна також задовольняти рівнянню Пуассона:

.

В магнітостатиці, як ми бачили в розділі 5 (див. (5.17)), векторний потенціал магнітного поля задовольняє саме умові кулонівського калібрування.