Rogers Computational Chemistry Using the PC

224	COMPUTATIONAL CHEMISTRY USING THE PC

the manuals available with any commercial compiler. SHMO was compiled with IBM FORTRAN Compiler 2.0 and also with Microsoft FORTRAN Professional Development System 5.1 (1991).

HMO is a more elaborate Huckel MO program than either MOBAS or SHMO. It calculates charge densities, free valency indices, and bond orders. It is written in FORTRAN and is a modification of a program by Greenwood (Greenwood, 1972). HMO must also be recompiled for different machines. The same two compilers work for HMO as for SHMO. The output of HMO is more compact than that of SHMO. For molecules of eight carbon atoms or fewer, the eigenvalues and eigenvectors fit onto the first screen. After responding to a PAUSE prompt, the total p electron energy, charge densities, free valency indices at each carbon atom, and bond orders are seen on the second screen. As presently formatted, HMO is limited to molecules of six carbon atoms or fewer to make the output compact, but this restriction can be released by changing the FORMAT statements and recompiling. A partial output for buta-1,3-diene is given in Fig. 7-6.

TOTAL PI-ELECTRON ENERGY= -4.4721 Charge densities

.0000 .0000 .0000 .0000 Free valency indices

.8376 .3904 .3904 .8376 Bond order matrix

1.0000 .8944 1.0000 .0000 .4472 1.0000 -.4472 .0000

.8944 1.0000

Stop - Program terminated.

Figure 7-6 HMO output for Buta-1,3-diene (second screen, condensed).

The total p electron energy is the sum of occupied orbital energies multiplied by two if, as is usually the case, the orbital is doubly occupied. The charge densities and free valency indices were treated in separate sections above. The bond order output should be read as a lower triangular semimatrix. The bond order semimatrix for the butadiene output is shown in Fig. 7-7.

		1.0000
		.8944	1.0000
	Figure 7-7 The Bond Order Semimatrix for	.0000	.4472	1.0000
		-.4472	.0000	.8944 1.0000
	Buta-1,3-diene.

The principal diagonal of the HMO output matrix is the p electron probability

density at atom j,	Na2	, where the summation is over all occupied orbitals. This
	ij		Na		a		. The electronic
as the bond order of atom j with itself
can be thought of P				ij		ij

P

charge times the electron probability density is the charge density at atom j, relative to a charge of 1.000 contributed by the 2p electron of the carbon atom, .0000 in the HMO output for buta-1,3-diene. The free valency index follows from Eq. (7-35).

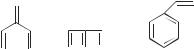
HUCKEL MOLECULAR ORBITAL THEORY II: EIGENVECTORS

225

The full bond order matrix is a symmetric tridiagonal matrix (Chapter 2). It is symmetric because the bond order Pjk ¼ P Naijaik is the same as the bond order Pkj ¼ P Naikaij. Elements off the tridiagonal (–.4472 in the butadiene example) are artifacts of the minimization and should be disregarded. The full bond order matrix for butadiene is

0	0:8944	1:0000	0:4472	0	1
B	1:0000	0:8944	0	0
	0	0:4472	1:0000	0:8944 C
B					C
@					A

00 0:8944 1:0000

There is slight disagreement (about 0.001b) between the bond orders in this output and those from Mathcad (see section on bond orders above) because of rounding error, different algorithms being used to determine the eigenvectors, and so on. In an approximate method such as this one, errors of this magnitude are negligible, although we shall soon be carrying out calculations where accuracy to the fifth digit beyond the decimal point is critical.

COMPUTER PROJECT 7-1 j Larger Molecules: Calculations using SHMO

SHMO, being in compiled FORTRAN, is much faster than MOBAS, which is written in standard interpreted BASIC. Solve the Huckel matrix for the hexatriene model using MOBAS and again using SHMO. Record the run time for this problem with each program. If you have a fairly new machine, this part of the project may not work. Both calculations may be so fast that you will not see the difference. From among the numerous problems presented up to this point, find one that is sufficiently demanding of computer iterations that you can tell the difference between the run times for interpreted BASIC and compiled FORTRAN. You will probably have to write your own programs in both BASIC and FORTRAN. Keep them as simple as possible. Coding and compiling FORTRAN programs is one of those things that isn’t much fun but should be done at least once or twice for the experience.

Use SHMO to obtain the energy spectrum for the models methylenepentadiene, bicyclohexatriene, and styrene. Draw all three energy level diagrams. Are there degeneracies for these molecules?

Polarographic oxidation entails removing one or more electrons from a molecule M undergoing oxidation at a mercury or similar electrode

M ! Mþ þ e ðoxidation of MÞ

226	COMPUTATIONAL CHEMISTRY USING THE PC

The more tightly held an electron is, the more difficult it is to remove, hence the higher the electrode potential necessary to remove it. Make the reasonable hypothesis that the electron removed in a one-electron oxidation comes from the highest occupied orbital, HOMO. Using SHMO, determine the HOMO for benzene, biphenyl, and naphthalene.

Note that all of the occupied orbitals in these molecules have negative energies, that is, they are below a by an energy measured in units of b. Electrons with the most negative b are most strongly bound and hardest to remove from the molecule. The molecule with the least negative HOMO has electrons that are highest in the energy spectra of these three relatively complicated molecules. These electrons are most easily withdrawn; hence, the molecule with the least negative b is most easily oxidized.

Arrange the three compounds in order of increasing oxidation potential. Plot the experimental value of oxidation potential, 1.3, 1.5, and 2.0 V for naphthalene, biphenyl, and benzene, respectively, vs. b for the HOMO of each compound.

COMPUTER PROJECT 7-2 j Dipole Moments

Using Program HMO, calculate the dipole moment of methylenecyclopropene by the HMO method. The program gives total charge densities at each carbon atom, making the calculation of dipole moments essentially a geometric problem. The single charge of the carbon atom must be subtracted from the total charge density to obtain the charge density used in the dipole moment calculation, that is, a computer output at carbon 1 of 1.5 leads to a p charge density at that atom of 0.5. Calculate the dipole moment of fulvene by the HMO method. Assume, for the calculation, that the endocyclic double bonds are parallel as in the diagram below and that the angle at carbon atom 2 is the same as in methylene-cyclopropene. These assumptions are not true, but we will be able to arrive at more accurate geometries and dipole moments by semiempirical and ab initio calculations. In which direction is the dipole moment of methylenecyclopropene? In which direction is the dipole moment of fulvene?

methylenecyclopropene fulvene

Program HMO gives you the option of modifying one or more of the elements input to the semimatrix. Calculate the charge densities of cyclopropeneone by entering the semimatrix

0	1	0	1
B	2		C

BC

@	0	1	0	0 A
	0	1	1

HUCKEL MOLECULAR ORBITAL THEORY II: EIGENVECTORS

227

and selecting the modification option by typing 01 at the prompt: Enter number of elements to be modified I2 format. Respond to the prompt: Enter row (I2), column (I2), and new element (F6.3) by typing

02011.414

This leads to the semimatrix

0	1
2	C
B 1:414 0

BC

@ 0 1 0 A

01 1 0

for cyclopropenone. Program HMO automatically loads the full matrix from the semimatrix because Huckel molecular orbital matrices are always symmetrical; hence, the program ‘‘knows’’ what the elements are above the principal diagonal. Calculate the dipole moment of cyclopropenone.

Use the same method to calculate the dipole moment of cyclopentadienone. Assume, for the calculation, that the endocyclic double bonds are parallel and the angle at carbon 2 is the same as in cyclopropenone.

O O cyclopropenone cyclopentadienone

There is a substantial difference in dipole moments between methylenecyclopropene and cyclopropenone, but the difference between fulvene and cyclopentadienone is much smaller. Explain.

COMPUTER PROJECT 7-3 j Conservation of Orbital Symmetry

Conservation of orbital symmetry is a general principle that requires orbitals of the same phase (sign) to match up in a chemical reaction. For example, if terminal orbitals are to combine with one another in a cyclization reaction as in pattern A, they must rotate in the same direction (conrotatory overlap), but if they combine according to pattern B, they must rotate in opposite directions (disrotatory). In each case, rotation takes place so that overlap is between lobes of the p orbitals that are of the same sign.

+−

−	+ − −	+
	+

Pattern A

++

− −	+ − −	+

Pattern B

228	COMPUTATIONAL CHEMISTRY USING THE PC

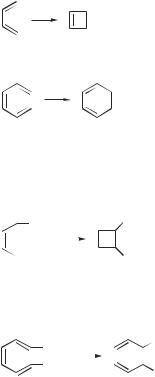
For this computer project, obtain the orbitals of butadiene and predict whether the cyclization of butadiene to cyclobutene is conrotatory or disrotatory.

Perform the same calculation for 1,3,5-hexatriene.

Conrotatory and disrotatory concerted reactions can often be distinguished by chemical means. For example, using the results of the previous calculation, predict whether the cyclizations of hexa-2,4-diene will lead to cis or trans dimethylcyclobutene

CH3			CH3
CH3			CH3

Perform the same calculation for cyclization of 2,4,6-octatriene. Which isomer of dimethylcyclohexadiene is formed?

CH3		CH3
CH3		CH3

COMPUTER PROJECT 7-4 j Pyridine

Heteroatoms have an electron density that is different from carbon. From an HMO point of view, the coefficient of the heteroatom in the secular matrix is larger or smaller according to whether the heteroatom is electronegative or electropositive relative to carbon. Empirical parameters may be used to augment or diminish the wave function through its coefficients, ai at the heteroatom j. The wave function (hence c2 and the electron probability density) can be augmented at the heteroatom only, as in the problem on pyrrole in Chapter 6, or for both the heteroatom and the carbon atoms immediately adjacent to it. In one approximation (Pilar, 1990), the input matrix for pyridine is

0	1:2	x	1	0	0	0	1
B	x þ 0:5 1:2		0	0	0	1:2	C
	0	0	1	x	1	0
B	0	1	x	1	0	0	C
B	0	0	0	1	x	1	C
B							C
B	1:2	0	0	0	1	x	C
B							C
@							A

HUCKEL MOLECULAR ORBITAL THEORY II: EIGENVECTORS

229

where the modifications a0r ¼ a þ hrb and b0rs ¼ krsb ¼ krs have been made to the secular matrix of benzene to account for the substitution of one nitrogen atom at the 1,1 position for one carbon atom. The parameters hr and krs for modifying a and b are based on electronegativity differences from carbon but are not particularly transferable to other problems. Transferability failure is one of the reasons that HMO methods have been largely abandoned in favor of methods described in Chapters 8 10. A thorough understanding of HMO methods is, however, a useful stepping stone to research-level ab initio and semiempirical molecular orbital calculations.

Procedure. Subtract xI from the input matrix above. Load the resulting upper semimatrix into MOBAS. The first element is 1,1,0.5,0. Recall that MOBAS requires entry of only the nonzero elements in the upper semimatrix. Obtain the eigenvalues and eigenvectors.

Repeat the procedure using HMO. HMO requires entry of the entire lower semimatrix, including the diagonal and all zero elements. Because the matrix element format is I1, only one symbol can be entered for each element. The numbers 0.5 and 1.2 cannot be entered in this format; instead enter 1, which will be modified later. The initial unmodified input for pyridine is the same as that for benzene, 010010001000010100010; hence, we can make a trial run on benzene to see if everything is working properly.

Run benzene using HMO. Write out the full bond order matrix, entering zero for any element off the tridiagonal. What is the bond order of benzene? Is there any Kekule-type alternation in this model?

To prepare the input matrix for pyridine, respond to the prompt asking how many elements should be modified with 03. Follow this with 01010.5 to change the 1,1 element to 0.5. Continue for the remaining two element changes. When the last element has been properly modified, the eigenvalues and eigenfunctions are calculated. Rerun to make sure you get the same answer.

Write out the tridiagonal matrix of charge densities (principal diagonal) and bond orders (upper and lower off-diagonals). What is the most active site in pyridine acting as a base? How might Cu2þ complex with pyridine? Is there a theory under which this might be regarded as an acid-base reaction? Is there much charge alternation in the pyridine ring? Is there much bond alternation in the pyridine ring?

PROBLEMS

1. Find the determinant of

cos y	sin y
sin y	cos y

2.Given the modified Huckel matrix and the orthogonal transform in Exercise 7-1, carry out the multiplication

AXA

and identify the product you get.

230	COMPUTATIONAL CHEMISTRY USING THE PC

3.Is the allyl coefficient matrix orthonormal?

4.Write out the coefficients of the butadienyl system, as they are produced by program MOBAS, in matrix form. Is the matrix symmetric? If not, can it be made symmetric by exchanging rows only?

5.Determine the eigenvectors and eigenvalues for methylenecyclobutene.

6.Determine the delocalization energy and dipole moment for methylenecyclobutene.

7.Draw charge density diagrams for the positive ion, free radical, and negative ion of the butadienyl system.

8.Draw bond order and free valency index diagrams for the butadienyl system.

9.Write a ‘‘counter’’ into program MOBAS to determine how many iterations are executed in solving for the allyl system. The number is not the same for all computers or operating systems. Change the convergence criterion (statement

300)to several different values and determine the number of iterations for

each.

10.Refer to Computer Project 7-2. Calculate b in units of electron volts using Wheland’s extension of Huckel molecular orbital theory.

11.Print Program MOBAS. Identify the statements in the program that generate the eigenvector matrix A by performing the same rotation operations on I that it performs on the input matrix to generate the eigenvalue matrix.

12.Determine the dipole moment of cyclobutenone.

13.Assuming a ð2sÞ2ð2pÞ2 electron distribution for the carbon atoms, calculate the energy of formation of ethylene from the gaseous atoms.

14.Spectroscopically determined values of b vary, but they are usually around2.4 eV. In the section on resonance stabilization, we saw that thermodynamic

measurements of the total resonance stabilization of butadiene yield 11 and 29 kJ mol 1 according to the reference standard chosen. Calculate the delocalization energy of buta-1,3-diene in units of b. Determine two values for the ‘‘size’’ of the energy unit b from the thermochemical estimates given. Do these agree well or poorly with the spectroscopic values?

15.The delocalization energy of benzene is 2b (verify this). From information in Exercise 7-6 calculate yet another value for the ‘‘size’’ of the unit b based on the thermodynamic values of the enthalpy of formation of benzene. Does this value agree with the thermodynamic values in Problem 14? Does it agree with the spectroscopic value?

C H A P T E R

8

Self-Consistent Fields

Because of its severe approximations, in using the Huckel method (1932) one ignores most of the real problems of molecular orbital theory. This is not because Huckel, a first-rate mathematician, did not see them clearly; they were simply beyond the power of primitive mechanical calculators of his day. Huckel theory provided the foundation and stimulus for a generation’s research, most notably in organic chemistry. Then, about 1960, digital computers became widely available to the scientific community.

Beyond Huckel Theory

To advance beyond Huckel’s method, we look again at the problem of calculating elements of the secular matrix. This is the problem Huckel simply swept away by setting the diagonal elements a equal to zero (as a reference point) and giving the basic energy unit the simplest possible definition: b ¼ 1 for adjacent carbon atoms and b ¼ 0 for nonadjacent carbons in alternant hydrocarbons. Huckel molecular orbital energies come out in units of b, but an indication of the inadequacy of the Huckel method is that evaluations of b for different molecular systems do not give the same results (Problems 15 and 16 in Chapter 7). The first systematic evaluation of all elements in the secular matrix for larger molecules by Hoffmann (1963) came

Computational Chemistry Using the PC, Third Edition, by Donald W. Rogers ISBN 0-471-42800-0 Copyright # 2003 John Wiley & Sons, Inc.

231

232	COMPUTATIONAL CHEMISTRY USING THE PC

about fully three decades after Huckel’s original work. About a decade earlier, Pople (1953) and others introduced the use of self-consistent fields into molecular orbital calculations. Both full-matrix and self-consistent field calculations rely heavily on computers.

Elements of the Secular Matrix

To begin a more general approach to molecular orbital theory, we shall describe a variational solution of the prototypical problem found in most elementary physical chemistry textbooks: the ground-state energy of a particle in a box (McQuarrie, 1983) The particle in a one-dimensional box has an exact solution

E ¼	n2h2	ð8-1Þ
	8ma2

and has an exact wave function

¼ A sinðkxÞ

ð8-2Þ

Let the dimension of the box be 1 in any units and consider only the ground state, for which n ¼ 1. Now

E ¼	h2		¼ 0:125	h2	ð8-3Þ
	8m			m

but, although we know the answer, we wish to test our approximation method by taking a linear combination of functions

c ¼ c1xð1 xÞ þ c2x2ð1 xÞ2

ð8-4Þ

which we shall write

c ¼ c1f1 c2f2

ð8-5Þ

There are two functions, so we shall obtain two eigenvalues. The ground-state energy will be the lower of the two. The full secular matrix is

H21	EjS21	H22	EjS22	ð j ¼ 1; 2Þ	ð8-6Þ
H11	EjS11	H12	EjS12

If we do not make any simplifying assumptions, we must calculate the matrix elements

H11 ¼ ð f1Hf1 dt	ð8-7aÞ
H12 ¼ ð f1Hf2 dt	ð8-7bÞ
H21 ¼ ð f2Hf1 dt	ð8-7cÞ

SELF-CONSISTENT FIELDS	233
and
H22 ¼ ð f2Hf2 dt	ð8-7dÞ

where the Hamiltonian operator for a particle in a box with the potential energy V ¼ 0 is

h2 d2

2m dx2

ð8-8Þ

In this problem, the integral over ‘‘all space’’ dt is in only one dimension, x. The limits of integration are the dimensions of the box, 0 and 1 in whatever unit was chosen.

Exercise 8-1

Calculate matrix element H11

Solution 8-1

d2

f1 ¼ xð1 xÞ

xð1 xÞ ¼ 2

2m

ð0 ð

dx2

ð0

ð

Þð

Þ

t

ð

Þ

Þ dx2

ð

Þ

t ¼ 2m

h2

1 x

1

x

d2

x 1

x d

h2

1 x

1

x

2

d

8-9

¼ m

2

3

0¼ m

6 ¼

6m

h2

x2

x3

1

h2

1

h2

Also, one needs to calculate the matrix elements

S11

¼ ð f1 f1 dt

ð8-10aÞ

S12

¼ ð f1 f2 dt

ð8-10bÞ

S21

¼ ð f2 f1 dt

ð8-10cÞ

S22

¼ ð f2 f2 dt

ð8-10dÞ

Again, the limits of integration are from zero to one.

Exercise 8-2

Calculate S11