Rogers Computational Chemistry Using the PC

134

COMPUTATIONAL CHEMISTRY USING THE PC

and

2k

k

o2A1 cos o t þ

A1 cos o t

A2 cos o t ¼ 0

m

m

ð5-9Þ

2

2k

k

o A2 cos o t þ

A2 cos o t

A1 cos o t ¼ 0

m

m

for the equations of motion, Eqs. (5-6) or (5-7). Dividing by cos o t, we get

2k

o2A1

k

¼ 0

A1

A2

m

m

ð5-10Þ

2k

2

k

A2

o

A2

A1

¼ 0

m

m

This is a pair of simultaneous equations in A1 and A2 called the secular equations

k

2k

o2

A1

¼ 0

m

m

A2

ð

5-11

Þ

m A1

þ m

o2 A2 ¼ 0

k

2k

which has, as its secular determinantal equation

m o2

m

0

5-12

2k

k

k

2k

2

¼

ð

Þ

o

m

m

a

b

¼ ad

bc.

We recall that expansion of a 2 2 determinant follows the rule

c

d

Expansion of the determinant in Eq. (5-12) leads to the quadratic

equation

2k

o2 2

k

2¼ 0

ð5-13Þ

mm

which has two solutions for the square of the frequency of oscillation

2k o2 ¼ k

mm

and

o2 ¼	2k		k	ð5-14Þ

mm

MOLECULAR MECHANICS II: APPLICATIONS

135

The two solutions for o2 are

o2 ¼

3k

;

k

ð5-15Þ

m

m

Two solutions for o2 lead to four solutions for o

¼ r

¼ r

¼ r

¼ r

ð

Þ

o1

3k

; o2

3k

;

o3

k

; o4

k

5-16

m

m

m

m

The general solutions for x1 and x2 are superpositions, that is, linear combinations of all of the solutions we have found

x1	¼ A1 cos o1 t þ A10	cos o2 t þ A100	cos o3 t þ A1000	cos o4 t	ð	5-17	Þ
x2	¼ A2 cos o1 t þ A20	cos o2 t þ A200	cos o3 t þ A2000	cos o4 t

but the amplitude constants in Eq. (5-17) are not all independent. We can get rid of some of them.

Going back to the secular Eqs. (5-10) or (5-11),

2k

o2A1

¼

k

A1

A2

m

m

ð5-18Þ

2k

2

k

A2 o

A2

¼

A1

m

m

substituting o2 ¼ k=m,

2k

k

¼

k

A1

A1

A2

m

m

m

ð5-19Þ

k

¼

k

A1

A2

m

m

which can be true only if A1 ¼ A2. Substituting o2 ¼ 3 k=m gives A001 same calculation for all eight amplitudes yields A1 ¼ A2; A01 ¼ A02; A001 A0001 ¼ A0002 . These simplifications lead to

x1 ¼ A1 cos o1 t þ A01 cos o2 t þ A001 cos o3 t þ A0001 cos o4 t x2 ¼ A1 cos o1 t þ A01 cos o2 t A001 cos o3 t A0001 cos o4 t

¼A002. The

¼A002, and

ð5-20Þ

There are now four constants rather than eight. We expect four constants from two second-order differential equations. Dropping the unnecessary subscript 1 and replacing the cumbersome ‘‘prime notation’’,

x1 ¼ A cos o1 t þ B cos o2 t þ C cos o3 t þ D cos o4 t

ð5-21Þ

x2 ¼ A cos o1 t þ B cos o2 t C cos o3 t D cos o4 t

136	COMPUTATIONAL CHEMISTRY USING THE PC

Normal Coordinates

The procedure we followed in the previous section was to take a pair of coupled equations, Eqs. (5-6) or (5-17) and express their solutions as a sum and difference, that is, as linear combinations. (Don’t forget that the sum or difference of solutions of a linear homogeneous differential equation with constant coefficients is also a solution of the equation.) This recasts the original equations in the form of uncoupled equations. To show this, take the sum and difference of Eqs. (5-21),

X1 ¼ x1 þ x2		ð	5-22	Þ
X2 ¼ x1 x2
we arrive at
X1 ¼ 2ðA cos o1 t þ B cos o2 tÞ		ð	5-23	Þ
X2 ¼ 2ðC cos o3 t þ D cos o4 tÞ
By the same double differentiation that gave us Eqs. (5-10),
€	2	ð5-24aÞ
X1	¼ o1X1
and
€	2	ð5-24bÞ
X2	¼ o3X2

which are just the equations we would get for uncoupled oscillators (Fig. 5-1a), except that the coordinates have undergone the linear transformations Eqs. (5-22). We should not be surprised that a transformation of the coordinate system leaves the solutions unchanged in Eqs. (5-22), leading to Eqs. (5-24). These new coordinates, X1 and X2, are called the normal coordinates.

Normal Modes of Motion

Let us take a 1.00-kg oscillator and couple it with an identical oscillator by means of a coupling spring of k ¼ 1:00 Nm 1. The force constants of the lateral springs are also 1:00 N m 1. Now the positive, real solutions for the frequencies are, from Eq. (5-15)

	¼ r			r		¼		p
o1; o3		k	;		3k		p
	m				m		1;		3

(Negative frequencies are physically meaningless.) Does this mean that one mass p

oscillates at 1:00 rad s 1 and the other at 3 ¼ 1:73 rad s 1? Not exactly. Behavior depends on the initial conditions. In the special case that both masses start from rest

MOLECULAR MECHANICS II: APPLICATIONS

137

a . . b . .

Figure 5-2 Synchronous and Antisynchronous Modes of Motion in a Bound, Two-Mass Harmonic Oscillator.

at the same displacement in the same direction, they will execute synchronous motion as in Fig. 5-2a, at 1:00 rad s 1. If the initial displacements are equal and

opposite (starting from rest also), they will execute antisynchronous motion at a p

frequency of 3 ¼ 1:73 rad s 1.

Two degrees of freedom lead to two modes of motion. These two modes of motion, synchronous and antisynchronous, are the normal modes of motion for this system. If only synchronous motion is excited, the antisynchronous mode will never contribute to the motion. The same is true for the pure antisynchronous mode (Fig. 5-2b); there will never be a synchronous contribution. Under these conditions, but only under these conditions, energy does not pass from one mass to the other.

In general, energy does pass from one normal mode to the other. If only one mass is displaced to amplitude A and released, it will excite motion in the second mass through the coupling spring until the second mass is oscillating with amplitude A. But, in the process, the first mass gradually loses all its energy until it stops. (Total energy is conserved.)

When the first mass has stopped, the situation is reversed. The second mass, oscillating at amplitude A, excites motion in the first mass, gradually losing its own energy, until it has excited the first mass back to amplitude A. This energy exchange, back and forth, goes on for ever (in the absence of friction). The envelope of amplitude of either mass in this exchange of energy is sinusoidal, with a frequency less than that of the individual masses. The frequency of transfer from one mode to the other is called the beat frequency.

If the masses are displaced in an arbitrary way or arbitrary initial velocities are given to them, the motion is asynchronous, a complex mixture of synchronous and antisynchronous motion. But the point here is that even this complex motion can be broken down into two normal modes. In this example, the synchronous mode of motion has a lower frequency than the antisynchronous mode. This is generally true; in systems with many modes of motion, the mode of motion with the highest symmetry has the lowest frequency.

138	COMPUTATIONAL CHEMISTRY USING THE PC

An Introduction to Matrix Formalism for Two Masses

The general case of two masses bound by two lateral springs k1 and k2, and coupled by a coupling spring, kc in Fig. 5-2b, has

m1€x1 ¼ Xi		fi ¼ k1x1 kcðx1 x2Þ ¼ ðk1 þ kcÞx1 þ kcx2						ð	5-25	Þ
m2€x2 ¼ Xj		fj ¼ k2x2 kcðx2 x1Þ ¼ kcx1 ðk2 þ kcÞx2
Eqs. (5-25) can be written in matrix form							x2
0 m2 €x2 ¼ ð			kþc		Þ	ðk2 þ kcÞ		ð5-26Þ
m1	0	€x1	k1	kc		kc	x1
or								ð5-27Þ
M €x2 ¼ K x2
€x1		x1

The rules of matrix-vector multiplication show that the matrix form is the same as the algebraic form, Eq. (5-25)

M€x ¼ Kx ¼ ðk1 þ kcÞ kc

kc ðk2 þ kcÞ

x2	¼	kcx1	ðk2 þ kcÞx2
x1		ðk1	þ kcÞx1 þ kcx2

ð5-28Þ

where M and K are matrices and lower-case bold €x and x designate vectors

€x ¼ €x1 €x2

and

x ¼	x2
	x1

Interest now centers on the matrix K. Equation (5-26) is general, but to introduce the method, let all springs have the same force constant. We have the matrix arising from the equations of motion,

	¼	k	2k	¼	1 2	ð		Þ
K		2k	k		k 2 1		5-29

which is the problem for symmetric and antisymmetric vibration that we have already solved.

MOLECULAR MECHANICS II: APPLICATIONS

139

If the coupling spring is missing [kc ¼ 0 in Eq. (5-28)], we get a unique diagonal

matrix	¼	0 k	¼	0 1	ð		Þ
K		k 0		k 1 0		5-30

leading to a pair of uncoupled equations,

m1€x1 ¼ kx1 m2€x2 ¼ kx2

Because the masses are the same, these equations describe independent oscillators with identical frequencies, as in Fig. 5-1a.

These matrices, for coupled and uncoupled oscillators,

	2	1		ð	5-31a	Þ
	1	2

and

1		0		;		ð	5-31b	Þ
0			1
have the roots
ð1; 3Þ;				coupled	and	ð1; 1Þ; uncoupled

Exercise 5-1

Find the roots of

2 1

12

Solution 5.4.1

Set

2 z 1

¼ 0

1 2 z

where z is the root. This leads to the quadratic equation

ð2 zÞ2 1 ¼ 0 ð2 zÞ ¼ 1

z ¼ 3; 1

Comparison with Eq. (5-15) enables us to identify the roots of the K matrix as z ¼ o2.

ð5-35Þ

140 COMPUTATIONAL CHEMISTRY USING THE PC

Taking the roots from Exercise 5-1, we can write them as the elements of a

diagonal matrix,		¼ m 0		X€2	¼ m X€2	¼ k 0	3 X2
0 m2	X€2		1
m1 0	€	1	0	€	€	1	0 X1
	X1			X1	X1

ð5-32Þ

where the simplifying assumption m1 ¼ m2 permits factoring m from the diagonal matrix M. The ordinary algebraic form of Eq. (5-32) is

€	¼ kX1
mX1					ð5-33Þ
€	¼ 3kX2
mX2
By comparison to Eqs. (5-23), it is evident that
o12 ¼		k			ð5-34aÞ
		m
and
o22 ¼		3k			ð5-34bÞ
		m

as found in Eq. (5-15). We have uncoupled the two original equations by diagonalizing the K matrix. Diagonalization reorients the coordinates to coincide with the vibrational modes, that is, it converts arbitrary coordinates to normal coordinates, Xi. We have determined the symmetric and antisymmetric frequencies by a matrix formalism that is readily generalizable to more complicated systems. Solving a determinantal equation and finding the roots of the corresponding matrix Eq. (5-32) amount to two ways of doing the same thing; we are solving simultaneous equations of the form Eqs. (5-11).

The Hessian Matrix

A single harmonic oscillator constrained to the x-axis has one force constant k that—stretching a point—we might think of k as a 1 1 force constant matrix. Two oscillators that interact with one another lead to a 2 2 force constant matrix

k11 k12 k21 k22

where the lateral spring 1 controlling mass 1 has a force constant k11, the other lateral spring has a force constant k22, and the connecting spring has a force constant k12 ¼ k21.

In a molecule, these latter two force constants are equal to one another because the coupling of atom 1 for atom 2 is the same as the coupling of atom 2 for atom 1.

MOLECULAR MECHANICS II: APPLICATIONS

141

The force constants k12 and k21 are the off-diagonal elements of the matrix. If they are zero, the oscillators are uncoupled, but even if they are not zero, the K matrix takes the simple form of a symmetrical matrix because k12 ¼ k21. The matrix is symmetrical even though k11 may not be equal to k22.

The force constants are second derivatives of the potential energy with respect to infinitesimal displacements of mass 1 and mass 2.

0

@

q2V		q2V
qx2		qx1qx2
1
q2V		q2V
qx2qx1		qx2
		2

1	ð5-36Þ
A

This kind of matrix is called a Hessian matrix. The derivatives give the curvature of Vðx1; x2Þ in a two-dimensional space because there are two masses, even though both masses are constrained to move on the x-axis. As we have already seen, these derivatives are part of the Taylor series expansion

f x

f a

Þ þ

f 0

a

Þð

x

a

Þ þ

f 00ðaÞ

ð

x

a

Þ

2

þ þ

f nðaÞ

ð

x

a

Þ

n

þ

ð Þ ¼

ð

ð

2

n!

in a one-dimensional x-space. If we drop all terms except the quadratic in the harmonic approximation and expand the function about the equilibrium atomic position a ¼ x0,

VðxÞ ¼ 1 d2V ðx x0Þ2

2 dx2 x0

as in Eq. (4-15) for one mass. For two masses in a one-dimensional space

dV ¼ 21	i;j	dqiqj 0qiqj
	2		d2V
	X

where qi and qj are mass-weighted generalized displacement coordinates

q		¼	pm1 x1; q2	pm1 y1; q3	pm1 z1; q4	pm2 x2; . . .
	1			¼	¼	¼

ð5-37Þ

ð5-38Þ

Mass weighting the generalized displacement coordinates qi and qj retains the form of Eq. (5-37) even when the actual masses are not unit masses.

If there were three masses moving on the x-axis and interacting with one another, the Hessian matrix would be 3 3

01

k11	k12	k13
k21	k22	k23	A	ð	5-39	Þ
@ k31	k32	k33

Two coupled masses oscillating in a plane have four degrees of freedom, x1, y1, x2, and y2 and so on (Fig. 5-3).

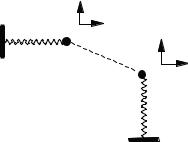
142	COMPUTATIONAL CHEMISTRY USING THE PC

1

y

x

2

Figure 5-3 Coupled Harmonic Oscillators in

the x-y Plane.

The Hessian matrix is

0 q2V

q2V

q2V

q2V

1

q2V

q2V

q2V

q2V

qx2

qy1qx1

qx2qx1

qy2qx1

B

1

C

q

2q

q2 1

q

2q 1

q

q

2q

5-40

B

q

q

q

C

ð Þ

B qx1qx2

qy1qx2

qx2

qy2qx2

C

B

x1

y1

y2

x2 y

y2

y1

C

B q2V

q2V

q2V

q2V

C

B

V

V

V

V

C

x

y

y

y

q

x

y

q

y2

B q

1q

2

q 1q

2

2q 2

2

C

@

A

A Hessian matrix for a molecule containing n atoms is more complicated. In the most general case, it is a very large 3n 3n matrix brought about because each atom moves in Cartesian 3-space. This large matrix can be constructed by starting out with elements for atom 1 in the first 3 rows (x, y, and z) and the first 3 columns of the matrix. This results in the 3 3 submatrix at the top left of the Hessian matrix, which gives the potential energy increase for atom 1 moving in its own 3-space, uncoupled to any other atom. The 3 3 submatrix immediately to the right, occupying rows 1 through 3 and columns 4 through 6, describes the energy of interaction (coupling) of atoms 1 and 2.

0

B B B B B B B B B B B B B B B B B

@

q2V

q2V

q2V

qq2V

qq2V

qq2V

1

q2V

q2V

q2V

2

2

2

qx2

qy1qx1

qz1qx1

q

V

q V

q

V

1

x2qx1

y2qx1

z2qx1

C

2V

q

2V

2V

q

2V

2V

q

2V

q

q

2

q

etc:

C

qx1qy1

qy2

qz1qy1

qx2qy1

qy2qy1

qz2qy1

C

qx1qz1

qy1qz1

qz1

qx2qz1

qy2qz1

qz2qz1

1

2

2

2

C

q

2V

q

2V

q

2V

q V

q V

q V

C

qx2

qy2qx2

qz2qx2

C

ð

5-41

qx1qx2

qy1qx2

qz1qx2

2

C

Þ

2

2

2

q

2V

2V

q

2V

C

q

V

q

V

q

V

q

2

C

qx1qy2

qy1qy2

qz1qy2 qx2qy2

qz2qy2

qy2

C

q

2V

q

2V

q

2V

2V

2V

2V

C

q

q

q

C

qx1qz2

qy1qz2

qz1qz2 qx2qz2

qy2qz2

2

qz2

. .

C

..

.

C

.

C

C

C

A

etc:	etc:

MOLECULAR MECHANICS II: APPLICATIONS

143

Diagonally below and to the right of the matrix containing only 1,1 subscripts is a 3 3 matrix containing only 2, 2 subscripts. It describes atom 2 independent of coupling. Continuing down the diagonal, one encounters a submatrix for atoms 3, 4, and so on. These are called block matrices. If all coupling submatrices are set equal to zero, only the block diagonal matrix remains.

etc.

Diagonalization of a block diagonal matrix is much easier and faster than diagonalization of the full matrix for structures significantly different from the equilibrium geometry because much of the work has already been done by setting the off-diagonal blocks to zero. This works because the bonding forces are much greater than the coupling forces. The coupling forces are not zero, however, and cannot be completely ignored in an accurate calculation. MM programs may be specifically written to begin by optimizing the block diagonal matrix and to switch over to a full matrix optimization when the geometry has been brought near the equilibrium geometry as determined by the size of the steps taken toward the equilibrium geometry.

Why So Much Fuss About Coupling?

The subject of force-coupled harmonic oscillation, leading inevitably to normal modes of motion and to the Hessian matrix, has been developed in far greater detail than other topics in molecular mechanics because the mathematical formalism is basic to almost everything we do in molecular computational chemistry, extending well beyond the classical mechanics of atomic vibrations. Virtually every mathematical technique described in this book uses some kind of minimization: minimization of the error in statistics, minimization of classical mechanical energy in molecular mechanics, or minimization of the electronic energy in molecular orbital calculations. Less frequently, in the study of reactive intermediates or excited species, a ‘‘saddle point’’ is sought. The term optimization can be used to include techniques that seek saddle points as well as minima. The term stationary point is used to denote the result of a generalized optimization procedure.