Rogers Computational Chemistry Using the PC

164	COMPUTATIONAL CHEMISTRY USING THE PC

change; hence, a small error in any of the computations going into rG is reflected in a large error in Keq. This inescapable exponential relationship must be borne in mind when evaluating calculated equilibrium constants and many other computed results in a practical or industrial context. However, lest we complain that nature has been unfair in placing such exacting demands on us for the accuracy of our calculations, let us be grateful that she permits us to do them at all.

Exercise 5-7: Calculation of Keq at 298 K

Because of the severe demands placed on us for accuracy if we are to calculate an equilibrium constant, let us choose a simple reaction, the isomerization of but-2-ene.

cis-but-2-ene ! trans-but-2-ene

Using MM3, calculate f H and S leading to rG and Keq. This reaction has been the subject of computational studies (Kar, Lenz, and Vaughan, 1994) and experimental studies by Akimoto et al. (Akimoto, Sprung, and Pitts, 1972) and by Kapeijn et al. (Kapeijn, van der Steen, and Mol, 1983). Quantum mechanical systems, including the quantum harmonic oscillator, will be treated in more detail in later chapters.

Solution 5-7

We found Keq ¼ 5:33 (mm3 cbu2.mm3, option 4, TEMP, VIB, VIB, Enter (default); read the output file using more TAPE4.MM3, hit spacebar to advance page by page to STATISTICAL THERMODYNAMICS). Kar, Lenz, and Vaughan calculated Keq ¼ 4:03. Kapeijn, van der Steen, and Mol found Keq ¼ 3:12, and an experimental study by Akimoto, Sprung, and Pitts produced Keq ¼ 2:98 at 298 K.

COMPUTER PROJECT 5-4 More Complicated Systems

Minimal input files for cyclopentene and cyclopentane can be constructed from a pentagon drawn on graph paper the way minimal ethylene was drawn (Fig. 4-4). For more complicated molecules, however, the draw function of PCMODEL or some similar file constructing program becomes less a convenience and more a necessity.

a)Cyclopentene. Calculate the enthalpy of hydrogenation of cyclopentene to cyclopentane and compare the result with hydH298 (ethylene) found in Computer Project 5-2. The result for hydrogenation of cyclopentene differs from that for ethene by an amount that is well outside the expected error for MM calculations. Suggest a reason for this.

b)Dimethylcyclopentene. The hydrogenation product of dimethylcyclopentene

CH3

CH3

+ H2		+

cis

trans

MOLECULAR MECHANICS II: APPLICATIONS

165

can exist in two forms, called cis or trans, according to whether the reaction product has both methyl groups on the same side of the plane of the cyclopentane ring or on opposite sides of the ring. (Most of the hydrogen atoms have been left out of the equation for simplicity.) The object of this part of the project is to compute thehydH298of the reactions leading to the cis and trans isomers and to compare them with the experimental value to see which of the isomers is actually formed.

Procedure. PCMODEL has a tool called Rings. Use this tool to establish a base molecule, either cyclopentene or cyclopentane. The Build tool converts a hydrogen atom into a methyl group, enabling you to build more complex molecules from simpler ones. Use Build to convert your base molecules to 1,2-dimethylcyclo- pentene, cis-dimethylcyclopentane, and trans-dimethylcyclopentane. Determinef H298 for all three molecules, and from these values determine which of the two reaction paths

CH3

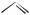
CH3

+ H2

cis

or

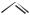
CH3

CH3

+ H2

trans

is followed. [In the actual experiment (Allinger et al., 1982), both are formed but one predominates.] The experimental value is hydH298 (1,2-dimethylcyclopen- tene) ¼ 22:5 0:2 kcal mol 1. This result is unusual, not only because it is a thermochemical analysis of parallel hydrogenation reactions, but because the enthalpy of hydrogenation is one of the smallest ever measured for a hydrocarbon. The reactant molecule is stabilized by methyl groups in the 1 and 2 positions, and the product, particularly the cis isomer, is destabilized by crowding. Both of these factors make hydrogenation less exothermic.

Among the unusual features of this reaction is that it is a surface-catalyzed reaction (Pd or Pt) but it gives a mixture of isomeric products. Suggest a mechanism by which this might occur.

c) Bicyclo[3.3.0]octane. If two cyclopentane molecules are fused at one bond

+ H2

166	COMPUTATIONAL CHEMISTRY USING THE PC

the product is bicyclo[3.3.0]octane. Bicyclo[3.3.0]octane can exist as cis and trans isomers according to whether the two hydrogen atoms at the ring fusion are on the same side of the molecular plane or on opposite sides of it. Moreover, in the cis isomer, the pentagons themselves are bent slightly out of the plane of the molecule such that, viewed edgewise, three conformers are possible

The object of this part of the project is to determine the energy (enthalpy) levels in each the three conformers and so to determine the composition of the equilibrium conformational mixture. That having been done for the cis isomer, the procedure is repeated for the trans isomer.

Procedure. Carry out a stochastic search on the cis isomer of bicyclo[3.3.0]octane to determine the relative energies of these three conformers. You need only the steric energies obtainable from STOCHASTIC.MEM for these relative energies because the summation of the bond energies is the same for all three conformers. Giving the lowest conformer an arbitrary zero energy, calculate the relative populations of the three states. You will need to match each energy with its structure.

Carry out the same stochastic search over the conformational space of the trans isomer. The result of this search may surprise you at first, but there is a simple explanation, which you should include in your report.

PROBLEMS

1.A 10.0-g mass connected by a spring to a stationary point executes exactly 4 complete cycles of harmonic oscillation in 1.00 s. What are the period of oscillation, the frequency, and the angular frequency? What is the force constant of the spring?

2.The electric field of electromagnetic radiation completes 4:00 1013 complete

cycles in 1.00 s. What are the period and frequency of the oscillation, and what is its wavelength? What is the frequency in units of cm 1?

3.The hydrogen atom attached to an alkane molecule vibrates along the bond axis at a frequency of about 3000 cm 1. What wavelength of electromagnetic

radiation is resonant with this vibration? What is the frequency in hertz? What is the force constant of the C H bond if the alkane is taken to be a stationary mass because of its size and the H atom is assumed to execute simple harmonic motion?

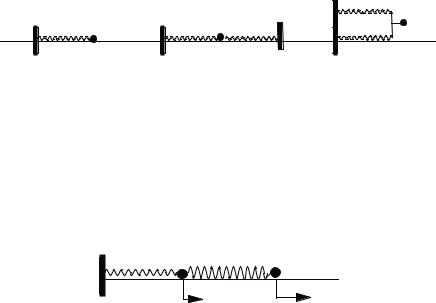
4.Three 10.0-g masses are connected by springs to fixed points as harmonic

oscillators shown in Fig. 5-12. The Hooke’s law force constants of the springs are 2k, k, and k as shown, where k ¼ 2:00 N m 1. What are the periods and

frequencies of oscillation in hertz and radians per second in each of the three cases a, b, and c?

MOLECULAR MECHANICS II: APPLICATIONS

167

			k
2 k	k	k	k
a		b	c
	Figure 5-12 Three Harmonic Oscillators.

5.Consider a harmonic oscillator connected to another harmonic oscillator (Fig. 5-13). Write the sum of forces on each mass, m1 and m2. This is a classic problem in mechanics, closely related to the double pendulum (one pendulum suspended from another pendulum).

6.Set up the classical equations of motion for the system in Fig. 5-13.

k1 m1	k2	m2
x1		x2

Figure 5-13 A Double Harmonic Oscillator. Displacements x1 and x2, shown positive, may also be negative or zero.

7.Write the equations of motion in matrix form. Take m1 and m2 to be unit masses (say 1.000 kg each).

8.For simplicity, take the specific case where k1 ¼ k2 ¼ k. Write the matrix of force constants analogous to matrix (5-29). Diagonalize this matrix. What are the roots? Discuss the motion of the double pendulum in contrast to two coupled, tethered masses (Fig. 5-1).

9.Write an expression for the kinetic energy T in a system of two masses connected by three springs including a central coupling spring. Write an expression for the potential energy V of this system. Write an expression for the total energy E. Note the similarity between this expression and the electronic Hamiltonian for helium, Eq. (8-17).

10.A spring stretches 0.200 m when it supports a mass of 0.250 kg.

(a) What is the force constant of the spring?

If the mass is pulled 0.0500 m below its equilibrium point and released:

(b)What is the frequency of harmonic oscillation of the mass? What is its period of oscillation?

(c)What is the potential energy of the mass at the extremes of its excursion?

(d)What is the maximum speed of the mass?

168	COMPUTATIONAL CHEMISTRY USING THE PC

11.Write and run an MM3 input file for methane ‘‘from scratch,’’ that is, open an empty file and put in all the necessary information to do the MM3 calculation on CH4. What is the enthalpy of formation of CH4? What are the C H bond lengths and angles?

12.Draw an enthalpy level diagram showing how Kistiakowsky was able to determine the value of isomH298 for the cis ! trans isomerization from enthalpies of hydrogenation.

13.What is the MM3 enthalpy of formation at 298.15 K of styrene? Use the option Mark all pi atoms to take into account the conjugated double bonds in styrene. Is the minimum-energy structure planar, or does the ethylene group move out of the plane of the benzene ring?

14.Find the MM3 enthalpy of formation of 1- and 2-methyladamantane. Use the Rings tool and the adamant option to obtain the base structure of adamantane itself. Use the Build tool to add the methyl group. 1-Adamantane is the more symmetrical structure of the two isomers.

15.What enthalpy difference would lead to a 25–75% mixture of syn and skew rotamers of 1-butene? Neglect any entropy change.

C H A P T E R

6

Huckel Molecular Orbital

Theory I: Eigenvalues

Most problems in chemistry [all, according to Dirac (1929)] could be solved if we had a general method of obtaining exact solutions of the Schroedinger equation

^ ¼

H E

^ ¼

The reason a single equation H E can describe all real or hypothetical

^

mechanical systems is that the Hamiltonian operator H takes a different form for each new system. There is a limitation that accompanies the generality of the Hamiltonian and the Schroedinger equation: We cannot find the exact location of any electron, even in simple systems like the hydrogen atom. We must be satisfied with a probability distribution for the electron’s whereabouts, governed by a function called the wave function.

We cannot solve the Schroedinger equation in closed form for most systems. We have exact solutions for the energy E and the wave function for only a few of the simplest systems. In the general case, we must accept approximate solutions. The picture is not bleak, however, because approximate solutions are getting systematically better under the impact of contemporary advances in computer hardware and software. We may anticipate an exciting future in this fast-paced field.

Computational Chemistry Using the PC, Third Edition, by Donald W. Rogers ISBN 0-471-42800-0 Copyright # 2003 John Wiley & Sons, Inc.

169

170 COMPUTATIONAL CHEMISTRY USING THE PC

Exact Solutions of the Schroedinger Equation

Among the few systems that can be solved exactly are the particle in a onedimensional ‘‘box,’’ the hydrogen atom, and the hydrogen molecule ion Hþ2 . Although of limited interest chemically, these systems are part of the foundation of the quantum mechanics we wish to apply to atomic and molecular theory. They also serve as benchmarks for the approximate methods we will use to treat larger

systems.
^	^

The Hamiltonian H in the equation H ¼ E is an operator, that is, it is an

instruction telling you what operation or operations to perform on some function, in this case, the wave function. The Hamiltonian takes a different form for different

	^
mechanical systems. One of the simplest forms of H is
^	h2 d2
H ¼	2m		dx2	þ V	ð6-1Þ

for a single particle of mass m constrained to move on the x-axis under a potential energy V. If V is zero for excursions of a particle between two limits in the x direction designated 0 and a but is infinite elsewhere, this form leads to the Schroedinger equation for what is called a particle in a one-dimensional box,

	h2 d2	ð6-2Þ
	2m dx2 ¼ E

The problem is treated in elementary physical chemistry books (e.g., Atkins, 1998) and leads to a set of eigenvalues (energies) and eigenfunctions (wave functions) as depicted in Fig. 6-1. It is solved by much the same methods as the harmonic oscillator in Chapter 4, and the solutions are sine, cosine, and exponential solutions just as those of the harmonic oscillator are. This gives the wave function in Fig. 6-1 its sinusoidal form.

Figure 6-1 Energy Levels E and Wave Functions for a Particle in a One-Dimensional Box.

	12
	10
	8
E	6
	4
	2
	0	a
	0
		x

HUCKEL MOLECULAR ORBITAL THEORY I: EIGENVALUES

171

The eigenvalues are discrete values of E, in this case 1, 4, 9, . . . units plotted as horizontal lines on the vertical axis in Fig. 6-1. The unit of energy in Fig. 6-1 is h2=8ma2, where h is Planck’s constant and a is the length of the permitted excursion of the particle along the x-axis. The eigenfunctions appear as sine waves having zero, one, or two internal nodes for the three eigenfunctions shown in Fig. 6-1. A node is a point where the function crosses the horizontal ( ¼ 0). All eigenfunctions for this system have two terminal nodes, one at either end. In general, the higher the energy eigenvalue of a system, the greater the number of nodes in the corresponding eigenfunction. There is an infinite number of possible energy values (solutions) for this system, but this is not the case for many other systems.

Another general observation that comes from consideration of simple systems like this one is that separation of discrete energy levels (quantization) appears when the motion of the particle is restricted in some way, in this case by placing barriers at x ¼ 0 and x ¼ a. A particle that is not constrained (free particle) is not quantized; its energy can take on any value. These general observations will be useful in understanding and interpreting more complicated systems.

All solutions of the Schroedinger equation lead to a set of integers called quantum numbers. In the case of the particle in a box, the quantum numbers are n ¼ 1; 2; 3; . . . . The allowed (quantized) energies are related to the quantum numbers by the equation

E ¼	n2h2	ð6-3Þ
	8ma2

The hydrogen atom is a three-dimensional problem in which the attractive force of the nucleus has spherical symmetry. Therefore, it is advantageous to set up and solve the problem in spherical polar coordinates r, y, and f. The resulting equation can be broken up into three parts, one a function of r only, one a function of y only, and one a function of f. These can be solved separately and exactly. Each equation leads to a quantum number

RðrÞ ) n
ðyÞ ) l	ð6-4Þ
ðfÞ ) m

These are three of the four quantum numbers familiar from general chemistry. The spin quantum number s arises when relativity is included in the problem, introducing a fourth dimension.

The hydrogen molecule ion is best set up in confocal elliptical coordinates with the two protons at the foci of the ellipse and one electron moving in their combined potential field. Solution follows in much the same way as it did for the hydrogen atom but with considerably more algebraic detail (Pauling and Wilson, 1935; Grivet, 2002). The solution is exact for this system (Hanna, 1981).

172	COMPUTATIONAL CHEMISTRY USING THE PC

In the few twoand three-dimensional cases that permit exact solution of the Schroedinger equation, the complete equation is separated into one equation in each dimension and the energy of the system is obtained by solving the separated equations and summing the eigenvalues. The wave function of the system is the product of the wave functions obtained for the separated equations.

Approximate Solutions

The logical order in which to present molecular orbital calculations is ab initio, with no approximations, through semiempirical calculations with a restricted number of approximations, to Huckel molecular orbital calculations in which the approximations are numerous and severe. Mathematically, however, the best order of presentation is just the reverse, with the progression from simple to difficult methods being from Huckel methods to ab initio calculations. We shall take this order in the following pages so that the mathematical steps can be presented in a graded way.

The simplest molecular orbital method to use, and the one involving the most drastic approximations and assumptions, is the Huckel method. One strength of the Huckel method is that it provides a semiquantitative theoretical treatment of ground-state energies, bond orders, electron densities, and free valences that appeals to the pictorial sense of molecular structure and reactive affinity that most chemists use in their everyday work. Although one rarely sees Huckel calculations in the research literature anymore, they introduce the reader to many of the concepts and much of the nomenclature used in more rigorous molecular orbital calculations.

We have said that the Schroedinger equation for molecules cannot be solved exactly. This is because the exact equation is usually not separable into uncoupled equations involving only one space variable. One strategy for circumventing the problem is to make assumptions that permit us to write approximate forms of the Schroedinger equation for molecules that are separable. There is then a choice as to how to solve the separated equations. The Huckel method is one possibility. The self-consistent field method (Chapter 8) is another.

Three major approximations are made to separate the Schroedinger equation into a set of smaller equations before carrying out Huckel calculations.

1. The Born--Oppenheimer Approximation

We assume that the nuclei are so slow moving relative to electrons that we may regard them as fixed masses. This amounts to separation of the Schroedinger equation into two parts, one for nuclei and one for electrons. We then drop the nuclear kinetic energy operator, but we retain the internuclear repulsion terms, which we know from the nuclear charges and the internuclear distances. We retain all terms that involve electrons, including the potential energy terms due to attractive forces between nuclei and electrons and those due to repulsive forces

HUCKEL MOLECULAR ORBITAL THEORY I: EIGENVALUES	173
among electrons. In chemical calculations, we usually	write the Schroedinger
^	¼ E , with the under-
equation in the same form as the original equation, H
standing that it now relates to electronic motion only.

The Born–Oppenheimer approximation is not peculiar to the Huckel molecular orbital method. It is used in virtually all molecular orbital calculations and most atomic energy calculations. It is an excellent approximation in the sense that the approximated energies are very close to the energies we get in test cases on simple systems where the approximation is not made.

Atomic Units

There is a very convenient way of writing the Hamiltonian operator for atomic and molecular systems. One simply writes a kinetic energy part 12 r2 for each electron and a Coulombic potential Z=r for each interparticle electrostatic interaction. In the Coulombic potential Z is the charge and r is the interparticle distance. The termZ=r is also an operator signifying ‘‘multiply by Z=r’’. The sign is þ for repulsion and for attraction.

The symbol r2 is an operator that takes the form

d2

dx2

in Cartesian 1-space,

r2 ¼ q2 þ q2 þ q2 qx2 qy2 qz2

in Cartesian 3-space, or a more complicated form in other coordinate systems that we might use, such as spherical polar or confocal ellipsoidal coordinates.

Writing 12 r2 for the kinetic energy of each electron amounts to taking our unit of mass as the mass of the electron instead of the kilogram (which is an arbitrary unit anyway) and defining h, the unit of angular momentum, as 1. The same thing can be done with the units of charge in an electrical potential, leaving V ¼ 1=r or V ¼ Z=r for multiply charged species. See Mc Quarrie (1983) for a table of atomic units and their SI equivalents. The atomic unit of energy in this system is the hartree, h ¼ 4:2359 10 18 joules, and the energy of the ground state of the hydrogen atom is exactly 12 h. Be careful not to confuse the unit h with Planck’s constant h.

The sum of two operators is an operator. Thus the Hamiltonian operator for the hydrogen atom has 12 r2 as the kinetic energy part owing to its single electron plus 1=r as the electrostatic potential energy part, because the charge on the nucleus is Z ¼ 1, the force is attractive, and there is one electron at a distance r from the nucleus

^	1	2	1		ð6-5Þ
H ¼ 2r			r