Преобразование хаара

Преобразование Хаара основывается на ортогональной матрице Хаара.

Ниже приведены примеры ортонормальных матриц Хаара четвертого и восьмого порядка:

Матрицы Хаара более высокого порядка строятся по тем же пра­вилам, что и матрицы H₄ и H₈. На рис. 6 приведены графики базисных функций преобразования Хаара при N = 16. Базисные изображения того же преобразования для матрицы отсчетов, содержащей 88 элементов, представлены на рис. 7.

Преобразование Хаара можно рассматривать как процесс дискретизации исходного сигнала, при котором с переходом к сле­дующей строке вдвое уменьшается щаг дискретизации.

Рис. 6. Базисные функции преобразования Хаара при N=16.

В задачах обработки изображений хааровский спектр описы­вает распределение энергии компонент соответствующих разно­стям яркостей соседних элементов, разностям средних значений яркостей соседних пар элементов и вообще разностям средних значений яркостей соседних групп из 2^m элементов.

На рис. приведен пример преобразования Хаара для конкретного изображения. На снимке с логарифмическим масшта­бом отчетливо заметна концентрация энергии, особенно в обла­стях с высокими секвентами. Отметим, что в спектре Хаара наб­людается концентрация энергии также в областях с низкими сек­вентами.

Преобразование карунена—лоэва

Метод преобразования непрерывных сигналов в набор некор­релированных коэффициентов разработан Каруненом и Лоэвом. Хотеллинг первым предложил метод преобразования дискретных сигналов в набор некоррелированных коэффициентов. Однако в большин­стве работ по цифровой обработке сигналов и дискретное, и непре­рывное преобразования называют преобразованием КаруненаЛоэва или разложением по собственным векторам.

В общем случае преобразование КаруненаЛоэва описы­вается соотношением

_{, (7)}

ядро А(j, k; и, v) которого удовлетворяет уравнению

, (8)

где K_F (j, k; j', k')  ковариационная функция дискретизованного изображения, а (и, v) при фиксированных и и v постоянна. Функции А(j, k; и, v) являются собственными функциями кова­риационной функции, а (и, v)  ее собственные значения. Как правило, выразить собственные функции в явной форме не удается.

Если ковариационную функцию можно разделить, т. е.

K_F (j, k; j', k') = K_C(j', j')K_R(k',k')

то ядро разложения КаруненаЛоэва также разделимо: А(j, k; и, v) = А_C(j, и) А_R(k,v)

Строки и столбцы матриц, описывающих эти ядра, удовлетворяют следующим уравнениям:

()

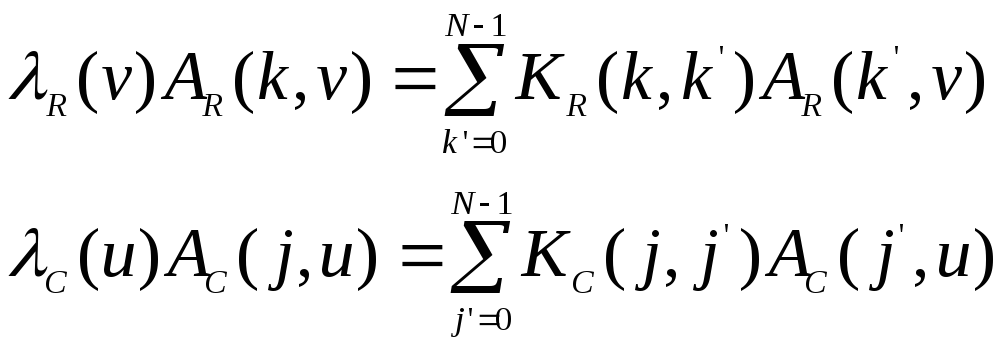В частном случае, когда ковариационная матрица описывает разделимый марковский процесс первого порядка, собственные функции удается записать в явной форме. Для одномерного мар­ковского процесса с коэффициентом корреляции  собственные функции и собственные значения имеют вид:

и _,

где 0j, иN-1, w(и)корни трансцендентного урав­нения