Жданов Явления переноса в газах и плазме 2008

1.10. Теплоемкость идеальных газов

Важной характеристикой газа является его теплоемкость. Теплоемкостью тела, как известно, называется величина, равная количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на один градус. При ее определении удобно исходить из записанного в дифференциальной форме первого закона термодинамики

′	(1.49)
d Q = dU + pdV ,

из которого следует, что подводимое к телу тепло Q расходуется

на изменение его внутренней энергии U и производство работы, связанной с изменением объема тела. Штрих при дифференциале d ′Q означает, что интеграл от этой величины нельзя представить в

виде разности конечного и начального значений, в отличие от dU , который является полным дифференциалом. Теплоемкость одного моля обозначается большой буквой C , при этом

	′
C =	d Q	.	(1.50)
	dT

Часто используются также значения удельных теплоемкостей, определяемых как отношение молярной теплоемкости к молекулярной массе газа ( c = C / M ).

Заметим, что под внутренней энергией тела U в термодинамике подразумевается энергия, приходящаяся как на поступательные, так и на внутренние степени свободы составляющих его молекул. Для идеального газа внутренняя энергия одного моля определяется тогда как

		3
	U = N A E	= RT		+ ε(T ) .	(1.51)
			2

Введем значения молярных теплоемкостей при постоянном объеме и постоянном давлении CV и C p . При этом на основании (1.49) и

уравнения состояния газа (1.6) имеем

C			∂U	,	C		= C + R .	(1.52)
		=
	V		∂T V			p	V

31

Для той части теплоемкости, которая определяется энергией, приходящейся на поступательные или транспортные ( tr ) степени свободы молекул, получаем

C tr	=	3	R ,	C tr =	5	R .	(1.53)
V	2			p	2

Именно такие значения имеют классические теплоемкости газа одноатомных молекул. Вклад в теплоемкость CV , связанный с внут-

ренними (int) степенями свободы молекул, определяется выражением [2]

	CVint = R	d	T ε(T )	= R[ε2	− ε 2 ] ,	(1.54)
		dT

где усреднение, как и в выражении (1.46) для ε , производится по

дискретному спектру значений внутренней энергии молекул. При учете вращательных и колебательных степеней свободы молекул имеем

где

CV = CVtr

+ CVrot

+ CVvib

,

(1.55)

rot

=

ε

rot

2

−

ε

rot

2

,

(1.56)

CV

R

)

(

rot

rot

Cvib = R

(εvib )2

−

εvib

2

.

(1.57)

V

vib

vib

При конкретных расчетах теплоемкости часто используются простые модели, описывающие внутреннее стояние молекулы. Так, вращательное движение двухатомной молекулы можно представить моделью жесткого ротатора, уровни энергии которого описываются выражением [3]

	EJ	=	=2	J (J +1) ,	(1.58)
			2I

где I – момент импульса молекулы. Вращательное квантовое число J принимает при этом значения J =0,1,2,…Расстояния между уровнями энергии не постоянны и возрастают в арифметической прогрессии.

32

Простейшей моделью, учитывающей колебательное движение атомов в двухатомной молекуле, является модель гармонического осциллятора, для которой [3]

			1
	Ev	= =ωvib v +		,	(1.59)
			2

где ωvib – собственная частота колебаний. Выражение (1.59) спра-

ведливо, когда в молекуле возбуждены не слишком высокие колебательные уровни, т.е. для сравнительно малых отклонений атомов от их положений равновесия. В этом случае расстояния между уровнями сохраняются постоянными. Применимость модели можно расширить, если учесть поправки на ангармонизм колебаний. В простейшем случае

Ev		1			1		2	(1.59')
	= =ωvib v +	2		− B=ωvib v +	2		,

где B – постоянная, зависящая от рода газа.

Рассмотрим сначала вклад в теплоемкость, связанный с вращательными степенями свободы двухатомной молекулы. Заметим,

что в соответствии с (1.58) в состоянии с		наименьшей энергией
J = 0 вращения	не возбуждены. В состоянии с J =1 имеем
E1 = =2 I . Если	kT << E1 , то это означает,	что средней тепловой

энергии молекулы недостаточно для возбуждения вращений, и вклад вращательных степеней свободы молекул в теплоемкость фактически отсутствует. В противоположном случае, когда kT >> E1 , возбуждается много вращательных уровней. Это означа-

ет, что при вычислении средних значений в выражении для CVrot

(1.56) основную роль в суммах играют члены с J >>1. Большим значениям J соответствует переход к квазиклассическому приближению, когда суммирование можно заменить интегрированием. Тогда, используя (1.43) и (1.58), находим

∞

Qrot ≈ ∫2J exp(− β0 J 2 )dJ = βo−1 , (1.60)

0

где β0 = =2 2IkT .

33

Вычисление (εrot )2

и

εrot

дает

rot

rot

(ε

rot

2

= (Q

)

−1

∞

2 2

2

2J β

J

exp

−β

J

dJ = 2

,

)

rot

∫

)

0

rot

( 0

(

)

0

εrot

rot =

(Qrot )−1

∞∫2J (β0 J 2 )exp(− β0 J 2 )dJ =1 .

(1.61)

0

Подставляя эти значения в формулу (1.56),

имеем: C rot

= R , что

V

соответствует классическому значению вращательной теплоемкости двухатомной молекулы. Напомним, что в классической теории теплоемкости используется теорема о равнораспределении энергии по степеням свободы, согласно которой на каждую степень свободы молекулы приходится энергия, равная (kT2). Поступательное

движение центра масс молекулы описывается тремя степенями свободы, поэтому соответствующая этому виду движения молярная

теплоемкость, как и в случае одноатомного газа, равна CVtr = (32)R .

Для двухатомной молекулы (модель гантели) должно учитываться вращение вокруг взаимно перпендикулярных осей, исключая вращение вокруг собственной оси, соединяющей две материальные

точки (атомы), поэтому CVrot = R и CV = CVtr + CVrot = (52)R .

В пределе низких температур (kT << =2 I ), сохраняя в суммах

лишь первые члены разложения при J = 0,1, получаем
CVrot = 3R(=2 I kT )2 exp(− =2 IkT ).	(1.62)

Если параметр I kT / =2 стремится к нулю, вклад вращательной составляющей в теплоемкость газа становится исчезающе малым.

В общем	случае	произвольных температур средние значения
(εrot )2	и εrot	можно рассчитать численно. Зависимость
rot		rot

CVrot / R от параметра β0−1 = (2IkT=2 )приведена на рис.1.5. [3].

34

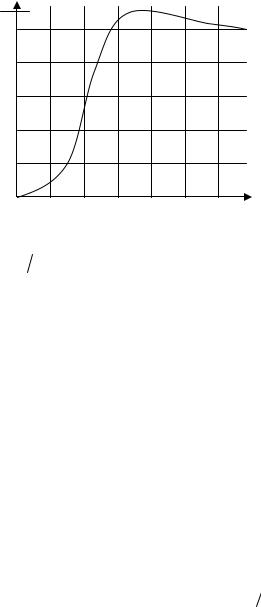
C rot

1.0R

0.8

0.6

0.4

0.2

0	0.4	0.8	1.2	2IkT
		Рис. 1.5	=2
Значения =2	2kI относительно велики лишь для легких газов
(85,4 К для H2	и 43,0 К для D2). Для N2		и O2 , например, они равны

соответственно 2,9 К и 2,1 К, поэтому при обычных (не очень низких) температурах значения вращательной теплоемкости для них имеют заведомо классические значения.

Рассмотрим теперь вклад колебаний молекул в теплоемкость двухатомного газа. Этот вклад становится заметным при температурах, более высоких, чем те, которые характерны для вращательной составляющей теплоемкости. Это связано со значительно большим значением кванта колебательной энергии (для комнатных

температур, как правило, =ωvib >> kT ). В том интервале температур, где можно пользоваться моделью гармонического осциллятора

(1.59), вычисление CVvib оказывается достаточно простым.

Благодаря быстрой сходимости рядов суммирование по v при определении средних значений можно формально распространить до v → ∞ . Если отсчитывать энергию от наиболее низкого (v = 0)

колебательного уровня, имеем [3]

	vib	∞			=ωvib			1
Q		= ∑exp		−		v	=				,
					kT			1 − exp(− =ωvib kT )
		v=0

35

2

=ω

vib

2

exp(=ω

vib

kT )+1

(εvib )

=

,

kT

(exp(=ωvib

kT )−1)2

vib

vib

=ωvib

kT

ε

=

.

(1.63)

vib

exp(=ωvib kT )−1

Выражение для колебательной составляющей теплоемкости принимает в этом случае вид

=ω

vib

2

exp(=ω

vib

kT )

C vib = R

.

V

kT

(exp(=ωvib

kT )−1)2

При низких температурах( kT << =ωvib )

C vib

=ω

vib

2

=ω

vib

= R

exp

−

.

V

kT

kT

(1.64)

(1.65)

Из формулы (1.65) следует, что при выполнении условия kT << =ωvib , величина CVvib становится очень малой. Фактически

это означает, что средняя тепловая энергия молекулы оказывается недостаточной, чтобы возбудить осциллятор, т.е. перевести его с нулевого (v = 0) на ближайший (v =1) энергетический уровень.

Возбуждение будет происходить только при столкновениях с молекулами, энергия которых значительно больше, чем средняя тепловая. Однако таких молекул относительно мало. В результате практически все осцилляторы останутся на низшем колебательном уровне. Таким образом, вкладом колебательной составляющей в полную теплоемкость газа при этих условиях можно практически пренебрегать.

При высоких температурах (kT >> =ωvib ) значение колебатель-

ной теплоемкости стремится к классическому пределу C vib	= R .
V

Это значение находится в соответствии с теоремой о равнораспределении энергии по степеням свободы, поскольку при гармонических колебаниях должна учитываться энергия, соответствующая как кинетической, так и потенциальной энергии колебаний атомов в молекуле. Средние значения этих энергий оказываются одинаковыми и равными (kT2). Учет двух колебательных степеней свобо-

ды и дает классическое значение молярной колебательной тепло-

36

емкости при постоянном объеме CVvib = N Ak = R для двухатомных

газов. Зависимость CVvib / R от параметра kT=ωvib приведена на рис. 1.6.

C vib

R

1.0

0.8

0.6

0.4

0.2

0	0.2 0.4 0.6 0.8 1.0 1.2 1.4	kT
		=ω

Рис. 1.6

Наконец, рассмотрим кратко вопрос о теплоемкости многоатомных газов. Молекула с тремя и более атомами обладает тремя вращательными степенями свободы и характеризуется в общем случае тремя главными моментами инерции I1 , I2 и I3 . Большое значе-

ние моментов инерции (и соответственно малое значение квантов вращательной энергии) позволяет при обычных температурах рассматривать вращение молекул как классическое. Применение теоремы о равнораспределении энергии по степеням свободы приво-

дит в этом случае к результату: CVrot = (3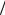2)R . Для линейных моле-

кул (независимо от числа атомов), обладающих, как и двухатомная молекула, лишь двумя вращательными степенями свободы и одним моментом инерции I , результат расчета будет таким же, как у двухатомного газа, т.е. классическое значение вращательной теп-

лоемкости CVrot = R .

При определении колебательной составляющей теплоемкости многоатомного газа, учитывается, что для колебаний, описываемых моделью гармонического осциллятора, колебательную энергию

37

молекулы можно представить в виде суммы энергий так называемых нормальных колебаний, каждое из которых характеризуется

собственной частотой

ω

k

. В результате значение C vib

получается

V

суммированием по всем колебательным модам.

C vib = R

∑k

=ω

k

2

exp(=ω

k

kT )

.

(1.66)

(exp(=ωk kT )−1)2

V

kT

В классическом пределе (kT >> =ωk )

каждое из нормальных ко-

лебаний дает

вклад в

теплоемкость,

равный

Ckvib = R ,

поэтому

CVvib = rR , где r – число колебательных степеней свободы. Для не-

линейной молекулы, состоящей из n атомов, r = 3n − 6 , для линейной n - атомной молекулы r = 3n − 5 .

1.11. Газовая смесь

Все обсуждавшиеся выше равновесные свойства простого (однокомпонентного) газа легко обобщаются на случай газовой смеси из N компонентов. При этом можно ввести функцию распределения молекул каждого из компонентов fα (v), нормированную на число-

вую плотность компонента α
∫ fα (v)dv = nα .	(1.67)

Числовая плотность смеси n определяется при этом простым суммированием

n = ∑nα .	(1.68)
α

В некоторых случая полезно использовать также определение массовой плотности компонента α

ρα = nαmα ,

(1.69)

где mα – масса молекулы сорта α . Массовая плотность смеси в целом определяется выражением

ρ = ∑ρα .	(1.70)
α

38

определяется выражением

pα , которое создает в газе каждый компонент смеси,

Для газовой смеси, находящейся в состоянии термодинамического равновесия, функция распределения fα по скоростям оказывается максвелловской функцией распределения вида

	m	α	3	2		m	α
fαM (cα )= nα					exp −			cα2		,	cα = vα −u . (1.71)
						2kT
	2πkT

Вид этой функции можно установить тем же способом, что и в случае простого газа, используя принцип детального равновесия, который записывается для переходов из одних скоростных интервалов в другие для парных столкновений как одинаковых, так и различающихся частиц.

Средняя кинетическая энергия компонента α , определяемая в системе отсчета, движущейся со скоростью u , записывается как

Eαtr =	∫(mαc2		2)fαM dc		=	3	kT .	(1.72)
	∫ f	M		dc		2
		α

Средние кинетические энергии хаотического движения частиц у всех компонентов смеси в равновесии оказываются одинаковыми, что является частным случаем классической теоремы статистической механики о равнораспределении энергии по степеням свободы частиц. Этим, в частности, объясняется тот факт, что в выражении для равновесной функции распределения (1.71) для любого компонента смеси фигурирует одна и та же температура T .

В состоянии равновесия одно и тоже значение для всех компонентов смеси имеет и макроскопическая скорость компонентов uα . Если определить последнюю с помощью выражения

nαuα = ∫v fαdv ,

(1.73)

то, подставляя в (1.73) функцию распределения (1.71), получаем uα =u , где u – макроскопическая скорость движения газовой смеси как целого.

Давление

pα = 2mα ∫(vx+ )2 fαM (v)dv .

(1.74)

39

Используя для fα (v) выражение (1.71) и производя вычисления, аналогичные выполненным в параграфе 1.7, получаем

	p α	=	2	n α E αtr	= n α kT .	(1.75)
			3
	Полное давление в газе определяется уравнением состояния

p = nkT = ∑nαkT ,	(1.76)
α
где использовано определение числовой плотности смеси (1.68).
В результате
p = ∑pα ,	(1.77)
α
что соответствует закону Дальтона (1.8).

Для газовой смеси, молекулы которой обладают внутренними степенями свободы, равновесная функция распределения компонента α по скоростям и внутренним энергиям молекул принимает

вид

m

α

3

2

1

m

α

E

αi

fα (c, Eαi )= nα

exp

−

c2 −

,

(1.78)

Qα

2kT

2πkT

kT

где

Qα = ∑exp(− Eα i kT ) .

i

Средняя энергия единицы объема смеси nE определяется сумми-

рованием соответствующих энергии поступательного и внутренне-
го движения молекул по всем компонентам смеси
n E = ∑nα (Eαtr		+	Eαint )=	3	nkT + kT		∑nα εα , (1.79)
α			2				α
где			∑εαi exp(− εαi )
	Eαint
εα =		=	i			.	(1.80)
	kT		∑exp(− εαi )

i

В силу аддитивности вкладов от каждого из компонентов в полную среднюю энергию смеси полная молярная теплоемкость смеси при постоянном объеме определяется выражением

40