Ктитров Расчет установившихся режимов и переходных процессов в нелинейных 2008

2

2

1

C mx

1

C mx

D

1

2

2

x

D

x

D

e

e

x

;

(3.42)

2 C

B

C m

x

C m

x

k

1

.

(3.43)

C

Dx

Dx

Для дисперсий запишем

( ) d ;

Dx

W1x (i )

2 Sn1

( )

W2x (i )

2 Sn2

(3.44)

2

2

Dy

(i )

(3.45)

W1y

Sn1 ( )

W2y (i )

Sn2

( ) d ,

где

T1(i )2 i Ti 1k

W

(i )

;

1x

T (i )2

(aTkk

1)i akk

1

1

1

W2x (i )

k(Ti 1)

;

T (i )2

(aTkk

1

1)i akk

1

1

W1y (i )

akk1(Ti 1)

;

T (i )2

(aTkk

1)i akk

1

1

1

W2y (i )

1

.

T (i )2

(aTkk

1)i akk

1

1

1

Вычисляя интегралы (3.45), (3.46), получим

D

x

(S1

S2 ) kk1

;

(3.46)

a(1 akk T)

1

Dy

S

2

(T T akk T2)

1

1

akk (T T 2T2akk )(1 akk T)

1

1

1

1

S1akk1(2T mkk1TT1)

.

(3.47)

(2T akk TT )1 akk (T T ) akk T2

1

1

1

1

1

Рассчитаем значения mx ,

Dx ,

Dy при следующих параметрах:

121

a 1; B C 0,1; T 0,8 c; T1 0,2 c; k =2; b 0,05; S1 4 10 3 ; S2 0,01.

Из (3.41), (3.47) получим

mxk0 (mx ,Dx ) =0,05;

D0,088k1(mx ,Dx ) .

x1 1,6k1(mx ,Dx )

Решая данную систему уравнений одним из численных методов (в данном случае – методом последовательных приближений), получим

mx 0,103, Dx 0,02, Dy 0,012.

Значение my вычисляется с помощью (3.41).

3.4. Расчет колебаний в нелинейных системах при случайных воздействиях

Важное значение имеет вопрос о влиянии случайных возмущений на параметры автоколебаний. На практике было замечено, что при определенной интенсивности случайного воздействия существовавшие в системе автоколебания прекращаются, это явление стали называть срывом автоколебаний.

Для определения параметров автоколебаний и условий их срыва при воздействии случайных возмущений применяется метод совместной статистической и гармонической линеаризации.

Будем считать, что на вход однозначной нелинейности поступает входной сигнал вида

x(t) mx A1 sin 1t+ x(t) ,	(3.48)

где x(t) – центрированный случайный процесс.

Сначала проведем статистическую линеаризацию нелинейности в соответствии с разд. 3.1, в результате получим

y(t)=F0 (mx+A1 sin 1t,Dx )+k1 (mx+A1 sin t,Dx ) x . (3.49)

Теперь перейдем к гармонической линеаризации слагаемых в (3.50). Разложим F0 и k1 в ряд Фурье, оставив члены ряда, обеспе-

чивающие линейность приближенного сигнала y(t) по A1 sin 1t и

122

x. Поскольку функция F0 обеспечивает передачу медленноменяющейся детерминированной составляющей входного сигнала, к которой относится и синусоида, то для нее следует учитывать члены ряда Фурье с нулевым и единичным индексами (2.8), (2.10), ко-

торые обозначим F0* и a1* соответственно.

В силу того, что k1 есть коэффициент передачи по быстроме-

няющейся случайной составляющей входного сигнала x, то для него следует учитывать только член ряда Фурье с нулевым индек-

сом, обозначаемый k1* . В результате получим приближенное выра-

жение для y(t):

y(t)=F0 (mx,Dx,A1)+q (mx,Dx,A1)А1 sin 1t+ k1 (mx,Dx,A1)x, (3.50)

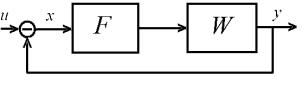
где q – коэффициент гармонической линеаризации (2.11). Рассмотрим систему, изображенную на рис. 3.4. Ее уравнение

имеет вид

Q(p)x R(p)F(x) Q(p)u ,

(3.51)

где u(t) mu u – случайное стационарное воздействие. Подставляя (3.48), (3.50) в (3.51) и приравнивая отдельно мате-

матические ожидания, колебательные составляющие и центрированные случайные составляющие, получим уравнения

Q(0)m	x	R(0)F* Q(0)m		u	;		(3.52)
		0
Q(p)A sin t R(p)q*A sin t 0						;	(3.53)
1		1	1		1
							(3.54)
Q(p)x R(p)k* x Q(p)u .
		1

Рис. 3.4. Структурная схема системы со случайным входом и автоколебаниями

123

Уравнение (3.53) будет иметь нетривиальное решение только в случае выполнения условий

		ReQ(i 1) R(i 1)q* 0 ;					(3.55)
Из (3.54) получим		ImQ(i 1) R(i 1)q* 0.					(3.56)
					2
		Q(i )
Dx					Su ( )d	,	(3.57)
		Q(i ) R(i )k
		1

где Su( ) – спектральная плотность случайного процесса u(t). Решая систему уравнений (3.52), (3.55)-(3.57) относительно не-

известных A1 , 1 , mx , Dx , получим параметры возможных авто-

колебаний и случайного процесса x(t) и, используя результаты разд. 3.3, получим также my , Dy . Решение данной системы воз-

можно в общем случае только численными методами, хорошие результаты показывает метод последовательных приближений.

Срыв автоколебаний в системе возможен при некоторых критических значений переменными mx , Dx . Для их достижения нужны определенные значения mu , Du , поэтому данная задача принципиально отличается от задачи о поиске параметров колебаний. В указанной системе уравнений необходимо положить A1 0 , что соответствует отсутствию колебаний. Тогда эта система будет решаться относительно неизвестных mx , Dx , Du , причем можно поло-

def

житьmu 0, поскольку автоколебания срываются из-за воздействия случайной составляющей входного сигнала. Одновременно определяется предельное значение 1, при котором происходит срыв колебаний. При найденных таким образом параметрах входного сигнала в систему существовавшие автоколебания будут сорваны. Основным среди найденных параметров будет минимальное значение Du , при котором происходит срыв автоколебаний.

124

Контрольные вопросы и упражнения

1.Для какого класса случайных процессов разработан метод статистической линеаризации?

2.В чем различие между первым и вторым вариантом метода статистической линеаризации?

3.Расчитайте коэффициенты по первому варианту метода статистической линеаризации для двухпозиционного реле с гистерезисом.

4.Почему функция Sx( ) называется спектральной плотностью мощ-

ности процесса x(t) ?

5.Какими двумя способами может быть вычислена корреляционная функция эргодического случайного процесса?

6.Для какого класса систем справедливо выражение, связывающее спектральную плотность входного и выходного сигналов?

7.Найдите спектральную плотность выхода системы с передаточной

функцией W(s)	1	и белым шумом с нулевым математическим

Ts 1

ожиданием и интенсивностью S0 .

8.Какой режим в динамической системе называется установившимся?

9.Являются ли линейные колебания установившимся режимом?

10.При каких условиях возможен расчет динамической системы с двумя случайными входными сигналами методом статистической линеаризации?

11.Какова последовательность применения методов статистической и гармонической линеаризации при их совместном использовании?

12.Что называется срывом автоколебаний?

13.Какой параметр входного сигнала определяет возможность срыва автоколебаний?

125

Глава 4. ОБОБЩЕННЫЙ МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ

4.1.Построение областей устойчивости нелинейных систем

впространстве их параметров

Рассмотрим нелинейную систему автоматического управления, достаточно полная модель которой может быть представлена системой n нелинейных нестационарных обыкновенных дифференциальных уравнений (ОДУ) следующего вида:

xˆ

с начальными условиями

ˆ		(4.1)
f (t,xˆ),

xˆ(0) xˆ0 X0 . Правая часть (4.1) в об-

щем случае должна удовлетворять условиям Филиппова [19] существования и единственности решения. Во многих случаях достаточно выполнения условия Липшица.

Система ОДУ (4.1) включает в себя как уравнения неизменяемой части САУ, так и изменяемой ее части, одним из главных ком-

понентов которой является управление uˆ (t,xˆ), обеспечивающее наилучшие показатели качества переходных процессов. Условия, которым должно удовлетворять качество, сформулированы в виде некоторого критерия Kˆ . В зависимости от конкретной системы множество значений Uˆ функции управления uˆ может быть как

замкнутым, так и открытым. Если множество Uˆ замкнуто, то это свойство можно задать двумя способами. Первый: записывается система неравенств вида

						i 1,...,r ,	(4.2)
uˆ		B(t,xˆ) B (t,xˆ) uˆ		B (t,xˆ) ,
			i	i	i	1

где B, Bi , Bi – заданные непрерывные по совокупности аргумен-

тов функции. Второй: управление uˆ задается в виде сложной функции

			uˆ (t,x) F [u~ (t,xˆ)],	(4.3)
		[u~ ]	0
где	F		– функции типа «ограничение». Причём Uˆ	– множе-
	0i

ство значений управления u~ (t,xˆ) – уже не является замкнутым и, 126

вообще говоря, не ограничено. В тех случаях, когда все или часть

компонентов вектора u~ являются кусочно-непрерывными функциями своих аргументов, их значения и величины левых и правых пределов в точках разрыва должны по модулю быть не меньше

B	и	B	.
i		i

				ˆ		является более
Второй способ задания границы множества U
естественным для прикладных задач, так как функции							F0i		вклю-
чаются как нелинейности в правую часть (4.1). Функция							F	[u~ ] в
							0i
пространстве переменных F			,u~ ,...,u~ определяет гиперповерх-
		0i	1	r
				1
ность, сечение которой плоскостью, проходящей через ось									0F0i ,
имеет описание
F0i (u~i )	1	|Bi | |Bi | |u~i Bi | |u~i Bi | ,							(4.4)
2

Поэтому далее условия замкнутости и ограниченности множества управлений специально оговариваться не будут, так как можно считать, что все ограничения учтены в выражении для правой час-

ти (4.1).

Явная зависимость правой части (4.1) от t учитывает не только нестационарность физического состояния САУ, но и присутствие ограниченных дифференцируемых в любой точке t (0, ) вход-

ных сигналов g1(t),...,gr2 (t) , r2 n. Если r2 n, то доопределим

вектор управляющих сигналов до размерности n с помощью нулевых компонентов и обозначим его g . Для большинства САУ можно установить взаимно однозначное соответствие между множест-

вом компонентов вектора	g и множеством компонентов вектора
x . Если каждая функция	gi (t) (i 1,...,n) определяет желаемый

вид функции xˆi (t), то вопрос о взаимно однозначном соответствии решен. Если же вместо переменных состояния имеется только r3 -

ˆ

мерный вектор выхода F[x(t)], а g (t) – заданный l3 -мерный желаемый вектор выхода, то n-мерный вектор, компонентами которого являются неизвестные функции g1(t),...,gn (t) , определяющие

127

желаемый вид функций xˆ1(t),...,xˆn (t) , может быть найден из следующей системы нелинейных алгебраических уравнений

g (t) F[g(t)] 0.

(4.5)

Как правило, компоненты функции выхода F являются линейными формами и поэтому найти g(t) нетрудно. Система (4.5) может иметь единственное или бесконечно много решений, что не влияет на физический смысл задачи, так как из имеющихся решений можно выбрать одно и для него установить соответствие с компонентами вектора x .

Таким образом, значения функции g(t) определяют в фазовом

пространстве Xˆ xˆ геометрическое место точек G (гладкое многообразие), на которое должна быть с помощью управления

u~ (t,x) переведена изображающая точка из начальной точки xˆ0 . В дальнейшем будем рассматривать два основных варианта САУ.

Первый вариант: управление U~ (t,x) существует и его удалось синтезировать известными методами, например основанным на принципе максимума или частотными методами (только для линейных систем). Тогда правую часть (4.1) можно представить в виде

		~
f			(t,xˆ		~	) .	(4.6)
	(t,xˆ) f			,g	,u

Для управляемых систем, удовлетворяющих условиям Филиппова (к ним относятся практически все реальные СУ), управление

u~ существует. Поскольку оно считается найденным как функция фазовых координат, то оно обеспечивает и стабилизацию системы, т.е. принадлежность изображающей точки множеству G на интервале (ty , ) , где ty – время выполнения задачи управления. Но

даже в этом случае для многих релейных нелинейных САУ задача регулирования не может считаться решенной в силу невозможности мгновенного переключения релейных элементов управления

u~ , которое, как правило, в нелинейных системах с ограничениями является кусочно-непрерывным.

Это приводит либо к появлению «неидеальностей переключения» (гистерезиса, чистого запаздывания и др.), либо к замене ку-

128

сочно-непрерывного управления u~ непрерывным управлением

U~ , U~ (t,0) 0, удовлетворяющим условию

~	~	(t,x)	,	(4.7)
U	(t,x) U

где заданная окрестность может быть сколь угодно малой. Если «двухпозиционное» реле по физическим причинам не может быть заменено непрерывным элементом, то с помощью последовательного соединения в систему вводится достаточно малая зона нечувствительности (в пределах допустимой статической ошибки), обеспечивая существование третьего, нулевого с точностью , значения реле, что требует построения дополнительных управлений, обеспечивающих удерживание изображающей точки в -окрестности

множества G . Замена управления u~ на u~ приводит к автоколе-

баниям. Если окрестность достаточно мала, то автоколебания имеют высокую частоту и малую амплитуду, что позволяет отнести их к классу вибраций. В данной работе будут исследоваться только системы, в которых вибрации недопустимы по соображениям безопасности, надежности и физической невозможности длительного функционирования исполнительных устройств САУ в таком режиме стабилизации.

Если для обеспечения физической реализуемости управления u~ радиус -окрестности увеличивать, то это приводит к сниже-

нию частоты и возрастанию амплитуды автоколебаний, что делает недостижимым как приемлемое качество переходных процессов, так и асимптотическую устойчивость системы.

В этом случае на параметры автоколебаний влияют не только «неидеальности» релейных переключателей, названные выше, но и все неустранимые существенные нелинейности, присутствующие в неизменяемой части системы.

Второй вариант: управление u~ (t,xˆ) существует, но его не удается синтезировать ни одним из разработанных к настоящему времени методов. Это прежде всего касается систем (4.1) с невыпуклой правой частью, так как для них, как правило, управление

u~ (t,xˆ(t)) (t) есть только измеримая функция времени (t) , по-

129

строенная с помощью тех или иных доопределений [20]. В этом

случае найти управление u~ как функцию фазовых координат можно только аналитически, так как численные методы в этом случае недостаточно эффективны. В настоящее время не разработано достаточно общих и конструктивных методов определения таких управлений для сложных существенно нелинейных САУ, в которые управление входит нелинейно. Однако даже решение этой задачи только приведёт от второго варианта САУ к первому варианту, что потребует решения проблемы автоколебаний.

Таким образом, для обоих вариантов САУ фундаментальной является проблема автоколебаний. Будем считать, что система ОДУ (4.1) в зависимости от конкретного случая может быть описанием САУ, относящихся к первому или второму варианту.

В идеальном случае задача стабилизации будет выполнена, если

каждый компонент вектора xˆ при t ty удовлетворяет условию

gi (t) xˆi (t) 0, i 1,..,n.

(4.8)

Однако в силу перечисленных выше причин условие (4.8) в реальных системах точно никогда не выполняется, поэтому заменим его на следующее условие

	gi (t) xˆi (t)	i , i 1,..,n,	(4.9)
введем новые переменные
xi (t) gi (t) xˆi (t), i 1,..,n,			(4.10)

и, подставив xˆi (t) gi (t) xi (t) в (4.1), получим новую задачу Коши

x	f (t,x);				(4.11)
			,
x	(0) x	0

в которой сигналы управления g(t) не играют самостоятельной роли, а считаются одним из нестационарных параметров правой

части

f(t,x) g(t 0) fˆ t,g(t) x(t), x0 g( 0) xˆ0; f(t,0) 0.

Данное преобразование переменных показывает, что любое явление, имеющее описание в виде системы ОДУ, может быть пред-

130