Ктитров Расчет установившихся режимов и переходных процессов в нелинейных 2008

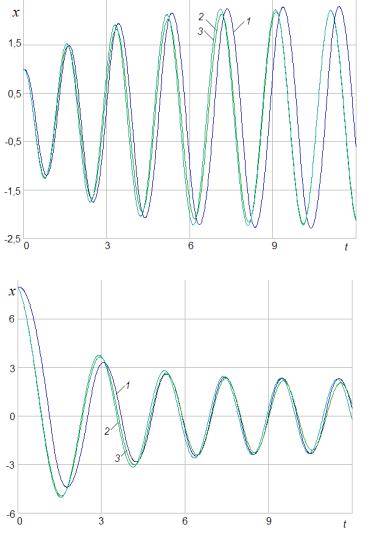
а

б

Рис 5.7. Переходные процессы в нелинейной системе, где 1 – численное моделирование с шагом по времени 0,01 с;

2, 3 – процессы, построенные методом экспоненциальной линеаризации с шагом по времени 0,1 с и с шагом по амплитуде 0,25 соответственно.

. а – установление автоколебаний с возрастанием амплитуды; б – установление автоколебаний с убыванием амплитуды

181

С другой стороны, качество нелинейной системы оценивается достаточно точно при шаге по времени, на порядок превышающем необходимый шаг численного моделирования. Применение методики дает приближенное аналитическое решение и позволяет проводить анализ качества семейства решений вне связи с начальными условиями.

Описанная методика позволяет без моделирования оценить показатели качества нелинейной системы, причем наличие аналитической связи показателей качества с параметрами линейной или нелинейной частей позволяет получить оценки качества как функции параметров системы. Даже если получение явной аналитической зависимости затруднительно, это позволяет избежать серийного моделирования и последующей обработки его результатов для оценки качества системы как функции ее параметров.

Следует отметить, что построение приближенного решения системы в зависимости от времени зачастую не требуется, а показатели качества переходного процесса, а именно показатель затухания и частота колебаний, определяются из (5.38) в форме выражений для и . Это позволяет без построения переходного процесса судить о качестве системы, прежде всего о времени протекания переходного процесса. Учитывая общность методов экспоненциальной и гармонической линеаризации, его следует применять, прежде всего, для оценки времени установления автоколебаний. Для наглядного представления показателей качества нелинейной системы, полученных методом экспоненциальной линеаризации, обычно используют диаграммы качества переходных процессов, являющихся обобщением областей устойчивости, рассмотренных как графическое представление параметров периодических режимов. Диаграмма качества представляет собой семейство линий уровня отдельно для и в координатах a и какого-либо параметра системы, что позволяет делать предположения о динамике системы при выборе этого параметра на этапе проектирования или изменении динамики системы при изменении этого параметра.

Примерный вид диаграммы качества представлен на рис. 5.8. Рис. 5.8, а построен для показателей затухания. Кривая 0, как указывалось ранее, представляет собой решение уравнений гармонического баланса и соответствует колебаниям с постоянной ам-

182

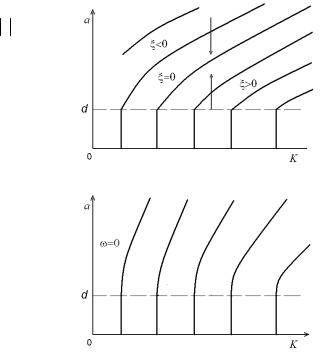
плитудой. Остальные кривые характеризуют связь параметров системы при некотором const . Для системы с постоянным параметром K переходный процесс на диаграмме будет отмечен вертикальной прямой, последовательно пересекающей линии с постоянным значением . Как и на областях устойчивости, направление движения обозначено стрелками, но в данном случае они избыточны, так как характер изменения амплитуды можно определить по знаку параметра .

На рис. 5.8, б представлена вторая часть диаграммы качества, состоящая из линий const . На обоих рисунках для a d линии постоянства показателей качества имеют вид вертикальных прямых, что означает независимость параметра от амплитуды при фиксированном K . Эта

область соответствует зоне линейности x d не-

линейного элемента. Действительно, в линейной системе 0 и 0 (см.

(5.13)) не зависят от амплитуды и определяются только корнями характеристического уравнения.

Часто требуется исследовать показатели качества переходного процесса, в установившемся режиме представляющего собой несимметричные колебания. В этом случае входной сигнал описывается в форме

x x0 asinψ,

отличающейся от (5.24) постоянной составляющей x0 , а выходной представляется в виде

а

б

Рис. 5.8. Примерный вид диаграммы качества

183

F(x, px) F0 (x0,a, , ) q(x0,a, , )x q (x0,a, , ) p x.

Выражения для коэффициентов экспоненциальной линеаризации (5.33), (5.34) следует модифицировать, добавив к входному сигналу x0 , а из дифференциального уравнения выделить уравнение для постоянной составляющей, как это делалось в МГЛ.

5.3. Модифицированный метод экспоненциальной линеаризации

Существенным ограничением методики, изложенной в разд. 5.2, является требование разделимости системы на одну линейную и одну нелинейную части, в связи с чем применение ее для анализа систем с двумя или более нелинейностями, разделенными линейными частями весьма проблематично. Другой недостаток метода экспоненциальной линеаризации – использование для аппроксимации переходных процессов кривых вида (5.13), которые соответствуют линейной системе второго порядка, что не позволяет описать сложные переходные процессы, возникающие в нелинейных системах высокого порядка.

Вгл. 4 описана модификация МГЛ, существенно расширяющая класс систем, для которых могут быть определены периодические процессы. Дополним модифицированный МГЛ (ММГЛ) средствами описания переходных процессов так, чтобы в частном случае при расчете процессов с постоянной амплитудой был бы получен ММГЛ. Для дальнейшего понимания читателю необходимо ознакомиться с гл. 4. Излагаемый подход назовем модифицированным методом экспоненциальной линеаризации (ММЭЛ).

Воснову ММГЛ положено разложение периодических функций в ряд Фурье с последующим представлением их частичными суммами ряда при расчетах. Одновременный учет нескольких гармоник позволяет описывать сигналы сложной формы во всех точках сопряжения линейных и нелинейных подсистем. Фактически линеаризация системы и запись уравнений гармонического баланса приводит к тем же уравнениям, что и приравнивание параметров сигналов на входе и выходе элементов элементарных линейных и нелинейных звеньев. Таким образом, для изложения ММЭЛ требу-

184

ется определить класс функций, описывающих сигналы между подсистемами и преобразование этих сигналов нелинейными и линейными звеньями. Уравнения же составляются как равенства параметров функций, описывающих сигналы в одной или нескольких точках полной системы. Учитывая нелинейный характер получаемых таким образом уравнений и большое число искомых параметров, получение решения в аналитической форме для большинства сложных систем (на применение для которых и ориентирован метод) затруднительно, если вообще возможно. Поэтому изложим ММЭЛ применительно к численному решению полученных уравнений.

Очевидно, что при анализе потребуется учитывать возможность существования разных показателей затухания для каждой локальной пары «нелинейность – линейная подсистема». В этом случае существенно, что на показатели затухания будет влиять и нелинейность, поэтому сигнал на выходе нелинейности представим выражением, учитывающим изменение амплитуды со временем (затухание).

Предположим, что основная частота колебаний известна, колебания на выходе нелинейности близки к установившимся. Представим выход нелинейности частичной суммой ряда Фурье

(2.5), (2.9)

		A0	n
	y		Ak sin(k t k ).	(5.50)
	2		k 1

Так как колебания все же не являются установившимися, для момента времени t t повторяя разложение в ряд, получим (5.50), но с другими параметрами. Предположим, что выход нелинейности в некотором смысле эквивалентен выходу линейной системы порядка n, не умеющей кратных корней. Тогда представив закон из-

менения амплитуд в виде Ak ak e kt , получим представление выхода нелинейности с учетом затухания в новой форме

		A0	n
	y		Ak exp( kt)sin(k t k ) .	(5.51)
	2		k 1

Замена нелинейности этой линейной системой и есть модифицированная экспоненциальная линеаризация, причем как будет показано далее, искать вид и параметры линеаризующей системы не требу-

185

ется – достаточно найти параметры выходного сигнала (5.51). Число слагаемых (экспоненциальных гармоник) n в (5.51) определяется требуемой точностью описания сигнала.

Выражение (5.51) не следует рассматривать как частичную сумму ряда, построенного, вообще говоря, не по системе ортогональных функций, а в качестве эмпирической формы, связывающей ряды Фурье, полученные для разных моментов времени. Здесь есть определенное внутреннее противоречие: значение выходного сигнала, представленное рядом, справедливо на отрезке времени, меньшем, чем отрезок разложения, определяемый частотой . Решение этой проблемы и обоснование допустимости такого подхода подробно рассмотрено в разд. 5.2 применительно к ряду Фурье и, следовательно, к его частичным суммам.

Показатель затухания, определяемый собственно нелинейностью, для каждой экспоненциальной гармоники определим по формуле:

k		ln Ak (tm 1) ln Ak (tm )	,	(5.52)
		t

где t tm 1 tm – достаточно малый промежуток времени, определяемый временем «достоверности» найденного решения, за который параметры k и k существенно не изменяются. В изло-

женном методе экспоненциальной линеаризации t соответствует шагу по времени. Величины Ak (tm), Ak (tm 1) – коэффициенты ряда Фурье, полученные для соответствующих моментов времени. Выражение (5.52) получено из представления амплитуд

Ak (tm 1) Ak (tm )e k t .

Необходимо пояснить, каким образом можно вычислить коэффициенты ряда Фурье, соответствующие одному конкретному моменту времени. Но прежде определим класс функций и метод определения их параметров, которые будут входными для нелинейности.

С учетом того, что линейные и нелинейные подсистемы группируются, на вход нелинейности поступает выход некоторой линейной части. В свою очередь, на вход линейной части поступает выход нелинейности (возможен и более сложный случай – сумма выходов линейной и нелинейной подсистем).

186

Таким образом, форму представления выхода линейной части сформируем на основе (5.51). Прохождение сигнала вида (5.51) через линейное звено приводит при точном вычислении к дополнительным слагаемым, определяемым полюсами линейного звена. Выход линейного звена запишем в следующей форме, учитывающей возможное наличие в линейной подсистеме корней с ненулевой мнимой частью и кратных корней:

		n		~	~	~ ~
x(t) A0 Ak					exp( kt)sin(k t k )+
	k 1
l	m(k)				~	~
	k	t	i				(5.53)
Bi				exp( kt)sin( kt k ).
k 0	i 0

Форма (5.53) пригодна и для описания реакции на сигналы вида (5.53) и их суммы с (5.51). Коэффициенты (5.53) могут быть найдены, например, с использованием операционного исчисления.

Вернемся к определению коэффициентов (5.51) и применению (5.52). Можно предложить два способа решения этой задачи. В соответствие с первым, который можно назвать методом замороженных коэффициентов, сумму (5.53) следует привести к виду

			M
		x(t			~	(5.54)
			,tm ) A0 Ak (tm )sin(k t k ),
			k 1
где		k (tm ) const	– коэффициент, полученный для времени tm
	A

подстановкой его в функции перед синусами в (5.53). Формируя (5.54) для моментов времени t tm и t tm 1 и раскладывая в ряд Фурье F(x(t,tm )), F(x(t,tm 1)), получаем представление (5.51) с

использованием (5.52). Согласно второму способу вход нелинейности представляется выражением (5.53) без предварительной модификации, а разложение выхода нелинейности F(x(t)) в ряд Фурье

производится по (2.5), (2.6) дважды на отрезках [tm T /2,tm	T /2]
и [tm t T /2,tm t T /2], где T 2 / . Если tm T ,	то раз-
ложение следует выполнять на отрезках [0,T] и [ t,T t].

Наличие обратных или перекрестных связей в системе позволяет записать уравнения баланса приравниванием соответствующих параметров и коэффициентов в (5.51) или (5.53) аналогично тому, как это делается в ММГЛ. Количество учитываемых гармоник и

187

форма представления должны совпадать только для приравниваемых сигналов. Остальные же сигналы в локальных парах «нелинейность – линейный элемент» могут иметь другое число гармоник, зависящее от свойств локальной пары. Их количество может определяться фильтрующими свойствами линейной части, быстротой затухания отдельных гармоник и т.п. Например, как было показано в гл. 2, при наличии фильтрующей линейной подсистемы на входе нелинейности следующей локальной пары сигнал можно представить одной гармоникой. При этом может потребоваться учесть большее число гармоник на выходе этой нелинейности, а их количество можно определять в процессе расчетов, сравнивая относительную амплитуду k -й гармоники с заранее заданным пороговым значением. Применимость сказанного для экспоненциальных гармоник очевидна, если принять во внимание алгоритм их формирования. Количество гармоник на выходе линейной системы хотя и определяется совокупностью входных и собственных гармоник, но может быть уменьшено, как и для нелинейности, с сравнением с пороговым значением.

Укажем теперь, какие параметры будут искомыми. Прежде всего, в системе следует выбрать точку, в которой сигнал может быть описан наименьшим числом экспоненциальных гармоник в форме (5.51). Искомыми будут частота колебаний , показатели затухания k , фазы k . Как и в методе экспоненциальной линеаризации, эти параметры можно считать зависящими от свободного параметра – текущей амплитуды первой гармоники рассматриваемого сигнала. Начальные амплитуды старших гармоник следует положить нулевыми. В этом случае число искомых параметров такое же, как и в ММГЛ. Если рассматривается процесс вблизи установившегося режима, найденного ранее с помощью ММГЛ, старшие гармоники следует взять из полученного решения. В противном случае число искомых параметров придется увеличить на количество учитываемых старших гармоник, добавив начальные значения их амплитуд.

Пример 5.4. Пусть передаточная функция линейной части

W(s) K . Предположим, на ее вход подается сигнал s

y(t) a0 exp( t)sin( t ),

188

являющийся выходом нелинейности после ее экспоненциальной линеаризации. На выходе линейного элемента с использованием операционного исчисления получим, считая const , const ,

const:

x(t) a0K(exp( t)sin( ψ) exp( t)sin( t ψ)) , (5.55)

			( )2 2
	где ψ arctg		. Подставляя в (5.55) tm и tm 1 (m – номер шага

по времени) всюду вместо t, за исключением функции sin, получаем для двух моментов времени вход последующей нелинейности в форме (5.54). Так,

x(t,tm ) a0 (tm) ) a(tm )sin( t (tm )),

где					exp( tm )
	a	(tm )										,
					( )2			2
	a	0 (tm )		a0K(exp( tm )sin(									ψ)	,
						( )2						2
		(tm ) arctg							.

Применяя (2.5), (2.6), дважды, используя (5.52), получаем входной сигнал для последующей линейной части в виде (5.51). Дополнительные слагаемые, определенные полюсами предшествующих линейных частей, не присутствуют в полученном выражении вида (5.51) выхода нелинейности. Для двузначной нелинейности F(x,x)

второй аргумент x(t,tm ) вычисляется подстановкой t tm в производную выражения (5.55). Продолжая таким образом, приходим к узлу системы, с которого вычисления были начаты. Приравнивая параметры в описании сигнала в данном узле до и после экспоненциальной линеаризации, получаем систему уравнений. Разность параметров «исходного» и «прошедшего звенья» сигналов позволяет построить функцию невязки для решения задачи методами нелинейного математического программирования.

189

Изложенная методика обобщает метод гармонической линеаризации (включая модификацию для сложных систем с нефильтрующими линейными частями) на случай быстрозатухающих переходных процессов. Этот подход позволяет получить связь показателей качества системы с ее параметрами и приближенно построить семейство типовых переходных процессов, задавая лишь начальную амплитуду, что существенно упрощает этап анализа системы, сокращая необходимые объемы моделирования. Так как построение переходных процессов возможно вести с шагом по амплитуде, а не по времени, методика позволяет также сделать обоснованные предположения о необходимом шаге моделирования по времени и проводить его с переменным шагом, что может существенно сократить требуемый объем вычислений.

5.4. Расчет параметров автоколебаний при неравномерной сходимости ряда Фурье

Изложенный в гл. 2 метод гармонической линеаризации и модифицированный метод гармонической линеаризации, представленный в гл. 4, позволяют решать задачи поиска и исследования автоколебаний для весьма широкого класса систем. Тем не менее, принятые допущения не позволяют применять МГЛ и его модификацию для ряда систем. Дополнительный учет специфических свойств таких систем позволяет еще более расширить область применения МГЛ.

Напомним, что в основу МГЛ, являющегося вариантом асимптотического метода Крылова – Боголюбова [9] и приводящего к эквивалентным результатам метода Пуанкаре [27], положено предположение о существовании решения в первом приближении, для чего накладывается условие фильтра. Для того чтобы решение существовало, линейная подсистема должна иметь как минимум третий порядок при однозначной нечетной нелинейности и второй, если нелинейность двузначная (см. метод шаблонов). Учет старших гармоник позволяет только уточнить решение, полученное в первом приближении. Кроме того, первое приближение ищется в форме линейных колебаний, для существования которых порядок системы не может быть меньше второго.

190