Ктитров Расчет установившихся режимов и переходных процессов в нелинейных 2008

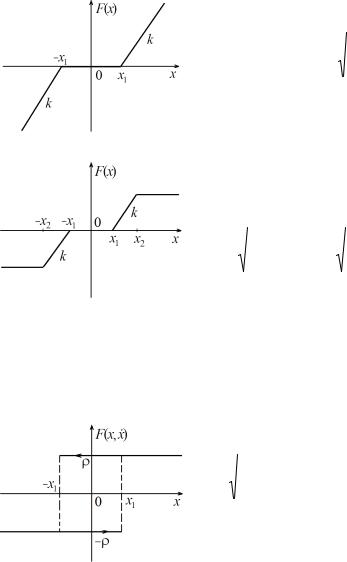
Окончание табл. 2.2

График нелинейности

q(A)

2k

x1

x1

x1

2

k

arcsin

1

A

A

A

при A x1

2

x

2

x

arcsin

arcsin

1

A

A

x2

x2

2

x1

x1

2

1

1

A

A

A

A

при A x2

Таблица 2.3

Коэффициенты гармонической линеаризации

типовых двузначных нелинейностей

График нелинейности

q(A)

q (A)

4

x

2

4 x1

1

1

A

A

A2

при A x1

при A x

1

41

Продолжение табл. 2.3

График нелинейности

q(A)

q

(A)

2

x2

2

1

A

A

2

x

x

x1

2

A2

2

1

1

A

при A x2

при A x2

k

arcsin( )

2

x

x

4kx

x

2

1

1

1

1

1

1

A

A

A

A

при A x1,

при A x

2x1

1

где 1

A

k

x

2

arcsin

A

arcsin

x1

A

4x1(x2 x1)

x2

x2

2

A

1

A

2

A

при A x2

x1

x1

2

1

A

A

при A x2

42

Окончание табл. 2.3

График нелинейности

q(A)

q (A)

k

x

2

x

arcsin

arcsin

1

A

A

x

2

1

x

2

2

4x1(x2 x1)

A

A

A2

при A x2

x1

x1

2

1

A

A

при A x2

Для приближенного вычисления коэффициента гармонической линеаризации q(A) в этом случае можно воспользоваться формулами квадратур Стеклова. Для таких нелинейностей

	2	/2
q(A)		F(Asin )sink d .
	A
		/2

Заменим переменную интегрирования, обозначив x Asin , тогда

d	dx			dx		, знаменатель положителен при
	Acos		A	1 (x/ A)2

~

. Также обозначим x/ A, F( F( . Тогда

2 2

1 ~

q(A) 2 F( ) d .

A 1 1 2

С использованием формулы квадратур Стеклова интеграл вида

	1	1	~
I				F( )					d вычисляется следующим образом:
				2
		1	1																~(6)
					1			~		~	~	1		~		1						( )
																			F
				I				F		(1) F	( 1) 2F			2F									.
																				5
					6						2								2		6!
																2

43

В итоге получим
2				A
q(A)		F(A) F			.	(2.19)
				2
	3A

Формула (2.19) является точной для нечетных нелинейностей, которые описываются полиномами до 5-го порядка включительно. В противном случае можно рассматривать аппроксимацию таким полиномом, и формула (2.19) становится приближенной. Для более точной оценки q(A) можно использовать формулу

1				A						3
q(A)		F(A) F					3F					A	,	(2.20)
	3A			2					2

полученную аналогично. Для полиномов до 11-й степени включительно (2.20) является точной.

Пример 2.2. Вычислим коэффициент гармонической линеари-

зации реле, 1. Применяя (2.11), получим q(A)

4

1,273

. По

A

4

1,333

A

формуле (2.12) q(A)

, что превышает точное значение

3A

A

на 5 %, а с использованием (2.13) q(A)

2

3

1,244

, что на 2 %

3A

A

меньше.

Пример 2.3. Построим зависимость амплитуды синусоиды на выходе гармонически линеаризованной нелинейности типа «ограничение» от амплитуды на ее входе. Нелинейность имеет k 1, x1 1. Обозначим амплитуду входной синусоиды через A, ампли-

туду первой гармоники ряда Фурье выхода нелинейности через A1.

Нелинейность является однозначной, поэтому для A x1 можно записать A1 q(A)A , где, с учетом параметров данной нелинейно-

	2			1	1				1	2
													A x1 справедливо
сти,	q(A)		arcsin				1					. При
				A		A
								A

A1 kA, или для данной нелинейности A1 A. Искомая зависимость представлена на рис. 2.4. Кривая качественно повторяет гра-

44

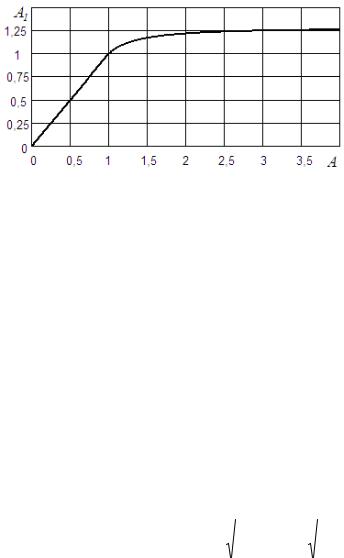
Рис. 2.4. Амплитуда на выходе линеаризованного ограничения

фик нелинейности, но насыщение наступает при большей, чем величина ограничения, амплитуде. Читателю предлагается построить аналогичный график для реле и объяснить результат.

Пример 2.4. Сравним результат прохождения синусоидального сигнала через активную и пассивную нелинейности типа «гистерезис с ограничением» (см. рис. 1.11) между собой и с первой гармоникой выходного сигнала.

На рис. 2.5 представлены графики, соответствующие пассивной и активной нелинейностям. На рисунке легко заметить запаздывание и опережение по фазе первой гармоники выходного сигнала относительно входного сигнала в пассивной и активной нелинейностях соответственно. Величину фазового запаздывания вычислим с использованием коэффициентов гармонической линеаризации

(A) arctg

q (A)

q(A)

arctg

4x1(x2

x1)

.

x2

x1

x2

x

2

x1

2

A

2k arcsin

arcsin

1

2

1

x1

A

A

A2

A

A2

A

Для активной нелинейности величина фазового опережения будет иметь противоположный знак.

45

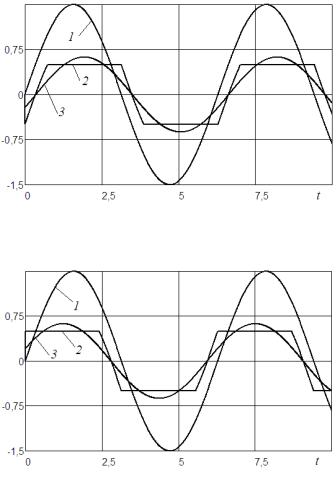
а

б

Рис. 2.5. Процессы в пассивной (а) и активной (б) нелинейностях: 1 – входной сигнал; 2 – выходной сигнал;

3 – первая гармоника выходного сигнала

46

2.2. Условия применимости метода гармонической линеаризации

Условия, при которых возможно применение гармонической линеаризации нелинейностей для расчета периодических установившихся режимов определим для системы, структурная схема которой приведена на рис. 2.1, следуя [8]. Входной сигнал u полагаем нулевым, передаточная функция (оператор линейной части)

имеет вид W(p) R(p) , R(p) и Q(p) – алгебраические много-

Q(p)

члены с вещественными коэффициентами, степень R(p) ниже сте-

пени Q(p) , F(x, px) – некоторая однозначная или двузначная нелинейность. Задача состоит в том, чтобы определить условия, при которых периодический сигнал x(t) достаточно близок к синусоидальному и может быть приближенно представлен в виде (2.4).

Запишем дифференциальное уравнение системы

Q(p)x R(p)F(x, px) 0.	(2.21)
Предполагаем, что существует периодическое решение	x уравне-

ния (2.21). Воспользуемся методом малого параметра [9]. Точное решение x представим рядом Фурье x x1 xB , где слагаемое x1

описывает первую гармонику и равно A1 sin t , высшие гармоники

обозначены через		xB Ak sin(k t k ) ,	– малый параметр.
		k 2
Тогда сигнал	на	выходе нелинейности	записывается так:
y F(x1 xB ,	px1 pxB ) . При гармонической линеаризации не-

линейности ее выход вычисляется на основе приближенного описания входного сигнала и полагается равным F(x1, px1). С исполь-

зованием разложения в ряд Тейлора по запишем их разность в следующем виде:

F(x, px) F(x1 xB , px1 pxB ) F(x1, px1)
		F(x , px )x				F(x , px )px		2 ... ...	(2.22)
			B				B
		1 1			px	1 1
x

Выражение (2.22) будет мало при малости или хотя бы ограниченности частных производных, что справедливо для большинства не-

47

линейностей, включая разрывные, так как в (2.22) используются значения производных в точке предполагаемого решения, которое может не совпадать с точками разрыва нелинейности. Кроме того, из предположения о близости x1 к решению системы следует ма-

лость xB . Разложим в ряд Фурье приближение выходного сигнала

F

F(x1, px1) F0

F1

1

p sin t Fk sin(k t fk )

(2.23)

k 2

и разность (2.22), дополняющую (2.23) до точного y :

G

F(x, px) G0

G1

1

p

sin t Gk sin(k t gk ).

(2.24)

k 2

Теперь подставим (2.23)

и

(2.24)

в (2.21), учитывая, что

x1 A1 sin t , xB

Ak sin(k t k ) :

k 2

Q(p)A1 sin t Q(p) Ak sin(k t k )

k 2

F

R(p)F0 R(p) F1

1

p sin t R(p) Fk sin(k t fk )

k 2

G

R(p) G0 G1

1

p sin t Gk sin(k t gk ) 0 .

k 2

Данное уравнение разделим на уравнения по гармоникам. Для постоянной составляющей получаем:

F0 G0 0,

откуда следует, что с точностью до должно выполняться F0 0 (сейчас мы рассматриваем колебания без постоянной составляющей, расчет систем с несимметричными колебаниями будет рассмотрен далее). Очевидно, это условие выполняется для нечетных нелинейностей.

Уравнение для первой гармоники, определяющее искомое приближенное решение таково:

				F						G
	Q(p)A sin t R(p) F			1		p sin t G				1	p sin t 0.(2.25)
	1		1					1

48

Откуда (см. выше о преобразовании линейной и линеаризованной нелинейной частями синусоидального сигнала в установившемся режиме), предполагая, что многочлен Q(p) не имеет чисто мнимых корней,

R(i )

R(i )

F

2

2

1

x1

A1 sin t

F1

sin

t

arg

arctg

F1

Q(i )

Q(i )

F1

R(i )

R(i )

G

2

2

1

G1

t arg

arctg

. (2.26)

Q(i )

G1

sin

G1

Q(i )

Как видно из (2.26) при решении уравнения (2.25), а следовательно, при приближенном решении (2.21) с точностью до , можно не учитывать поправку (2.22).

Теперь рассмотрим условия, при которых уравнения для высших гармоник можно не учитывать. Запишем уравнения при k 2,3,...

Q(p) Ak sin(k t k ) R(p)Fk sin(k t fk )

R(p) Gk sin(k t gk ) 0.

(2.27)

Выразим, аналогично (2.26),

k -ю гармонику:

R(ik )

R(ki )

x

k

A

sink t

F

sin k t f

k

arg

k

Q(ik )

k

Q(ik )

R(ik )

R(ik )

G

k

sin k t g

k

arg

.

(2.28)

Q(ik )

Q(ik )

Из (2.28) следует, что для малости k -х гармоник (которые мы собираемся отбрасывать при расчетах) необходимо, чтобы множи-

тель R(ik ) Fk был достаточно мал. Сравнивая (2.28) и (2.26), за-

Q(ik )

ключаем, что при сопоставимых по величине Fk и F12 F1'2 , а

это справедливо для многих существенных нелинейностей, по крайней мере, для небольших k (см., например, табл. 2.2), для того чтобы можно было считать (2.28) пренебрежимо малым порядка , необходимо потребовать выполнения условия:

	R(ik )		R(i )	,	(2.29)
	Q(ik )		Q(i )

49

которое принято называть условием фильтра, или гипотезой фильтра. Физически условие (2.29) означает, что амплитуды синусоид, составляющих ряд Фурье сигнала на выходе нелинейности на старших частотах, кратных основной частоте, частоте колебаний, усиливаются линейной частью существенно меньше, чем первая гармоника. Гипотезой же (2.29) называют, потому что для проверки выполнения условия (2.29) необходимо знать , которую получают, применяя МГЛ. Таким образом, возможность применения метода обосновывается только после его применения. Оценить, будет ли справедливо (2.29) до определения , можно по виду амплитудной частотной характеристики линейной части. Для того, чтобы она убывала, потребуем, чтобы порядок многочлена R(p) по p

был меньше порядка Q(p) .

Итак, перечислим условия, которым должна удовлетворять система, для применения МГЛ при определении колебаний, приближенно описываемых одной гармоникой.

1.Разделимость системы на статический нелинейный элемент

илинейную часть.

2.Выполнение условия фильтра (2.22).

3.Отсутствие корней Q( ) 0, таких, что Re 0, Im 0.

4. Ограниченность частных производных нелинейности

F(x, px) и F(x, px) за исключением, быть может, множест-

x px

ва точек меры нуль.

5. Отсутствие постоянной составляющей на выходе нелинейного элемента (для симметричных колебаний).

Приведенные условия сформулированы для основного варианта МГЛ. Модификации МГЛ, для которых они существенно ослаблены, приведены в гл. 4 и 5.

2.3. Применение метода гармонической линеаризации для расчета симметричных колебаний

Опишем порядок расчета параметров симметричных автоколебаний в системе, имеющей структурную схему, приведенную на

50